İçindekiler

İçindekiler
Geometri Nedir?
v
Bölüm 1. GEOMETRİK KAVRAMLAR
1
1. NOKTA, DOĞRU, DOĞRU PARÇASI VE IŞIN
2
2. DÜZLEM ve İLGİLİ AKSİYOMLAR
5
Bölüm 2. AÇILAR
9
1. AÇILARLA İLGİLİ GENEL KAVRAMLAR
9
2. PARALEL İKİ DOĞRUNUN BİR KESENLE YAPTIĞI AÇILAR 12
3. KENARLARI PARALEL OLAN AÇI ÇİFTLERİ
14
4. KENARLARI BİRBİRİNE DİK OLAN AÇI ÇİFTLERİ
16
Bölüm 3. ÜÇGENLER
19
1. ÜÇGENLE İLGİLİ TEMEL KAVRANLAR
19
1.1. Üçgenle İlgili Tanımlar:
19
1.2. Kenarlarına Göre Üçgen Çeşitleri
20
1.3. Açılarına Göre Üçgen Çeşitleri
20
1.4. Üçgende Yardımcı Elemanlar
21
2. ÜÇGENDE AÇILAR
22
2.1. Üçgende Kenarlar ile Açılar Arasındaki Bağıntılar
24
3. ÜÇGENLERDE EŞLİK KAVRAMI
26
3.1. Üçgenlerde Eşlik Aksiyomları
26
4. ÜÇGENLERDE BENZERLİK KAVRAMI
31
5. ÜÇGENLERDE AÇIORTAY TEOREMLERİ
34
6. ÜÇGENLERDE BENZERLİK TEOREMLERİ
36
i
ii
İÇINDEKILER
7. DOĞRU PARÇALARININ UZUNLUKLARI ARASINDAKİ
ORAN VE ORANTI
8. DİK ÜÇGENLERDE METRİK BAĞINTILAR
Bölüm 4. DÖRTGENLER
39
44
49
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
50
1.1. Yamuk
51
1.2. İkizkenar Yamuk
53
1.3. Paralelkenar
54
1.4. Eşkenar Dörtgen
55
1.5. Dıkdörtgen
55
1.6. Kare
56
1.7. Deltoid
57
2. ÇOKGENLER
58
2.1. Dişbükey ve İçbükey Çokgenler
58
2.2. Düzgün Çokgenler
59
Bölüm 5. ÇEMBERLER
63
1. ÇEMBERLE İLGİLİ KAVRAMLAR
63
2. ÇEMBERİN DÜZLEMDE AYIRDIĞI BÖLGELER
64
3. BİR DOĞRU İLE BİR ÇEMBERİN BİRBİRİNE GÖRE
KONUMLARI
65
4. İKİ ÇEMBERİN BİRBİRİNE GÖRE KONUMLARI
66
4.1. Kesişmeme Durumu
66
4.2. Teğet Olma Durumu
67
4.3. Kesişme Durumu
67
5. ÇEMBERDE YAYLAR VE AÇILAR
68
5.1. Merkez Açı
68
5.2. Çevre Açı
69
5.3. Teğet-Kiriş Açı
71
5.4. İç Açı
71
İÇINDEKILER
5.5. Dış Açı
iii
72
6. ÇEMBERDE YAY ve TEĞET PARÇALARI UZUNLUĞU
HESABI
73
6.1. Çemberde yay parçası uzunluğu
73
6.2. Çemberde teğet parçası uzunluğu
74
6.3. İki çemberin ortak teğetleri
75
7. KUVVET, KUVVET EKSENİ ve KUVVET MERKEZİ
77
7.1. Bir Noktanın Bir Çembere Göre Kuvveti
77
7.2. İki Çemberin Kuvvet Ekseni
79
7.3. Kuvvet Merkezi
81
8. ÇOKGENLER ve ÇEMBERLER
83
8.1. Üçgen ve Çember
83
8.2. Dörtgenler ve Çemberler
85
9. GEOMETRİK YER KAVRAMI ve BELİRLENMESİ
86
Bölüm 6. ALAN HESABI
90
1. ÇOKGENSEL BÖLGELERİN ALANI
91
1.1. Karenin Alanı
91
1.2. Dikdörtgenin Alanı
91
1.3. Dik Üçgenin Alanı
92
1.4. Üçgenin Alanı
92
1.5. Paralel Kenarın Alanı
94
1.6. Yamuğun Alanı
94
1.7. Deltoidin Alanı
95
1.8. Düzgün Çokgenlerin Alanı
95
2. DAİRESEL BÖLGELERİN ALANI
97
2.1. Dairenin Alanı
97
2.2. Daire Diliminin Alanı
97
2.3. Daire Parçasının Alanı
98
2.4. Halkanın Alanı
99
iv
İÇINDEKILER
Bölüm 7.
KATI CİSİMLERİN ALAN ve HACİM HESAPLARI
101
1. PRİZMALAR
101
2. PİRAMİTLER
105
3. SİLİNDİR
111
4. KONİ
113
4.1. Koni Çeşitleri
114
5. KÜRE
117
5.1. Kürenin Belirlenmesi
117
5.2. Kürenin Alan ve Hacminin Hesaplanması
118
5.3. Küreden Elde Edilen Kavramlar
122
Index
131
Geometri Nedir?
Geometri Yunanca geo (yer) ve metri (ölçü) anlamına gelen, düzgün
şekillerin ve cisimlerin özeliklerini ve aralarındaki ilişkileri inceleyen bilim
dalıdır. Kullanılan aksiyomlara göre isimler alan değişik geometriler vardır.
Biz bu derste paralellik bağıntısı üzerine kurulan ve Öklid Geometrisi olarak
bilinen düzlemsel konuları ele alacağız.
Geometri düşünmeyi kolaylaştıran ve problemi şekille gözünde canlandıra
rak çözüme ulaşmayı sağlayan bir bilim dalıdır. Günlük hayatta insanların
çözmek zorunda kaldığı basit problemlerin pek çoğunun çözümü temel geometrik beceriler gerektirir.
Geometri aynı zamanda bireyin yaşadığı dünyayı algılamasında ve diğer
matematik konularına bakış açısında bir köprü rolü oynar. Çünkü matematik
öğretiminde soyut olan bazı kavramların somutlaştırılarak sunulması gerekliliği, yarı-somut olarak adlandırabileceğimiz geometrik yapıların bu süreçte ne
derece önemli olduğunu göstermektedir.
Bu kitap, eğitim fakülteleri ilköğretim bölümü matematik öğretmenliği
öğrencilerine, yani matematik öğretmeni olmaya meyletmiş öğretmen adaylarına ilk ve orta öğretimde öğrendikleri geometri konularını bir başkasına
öğretebilecek şekilde ele alarak, bilinen bazı teorem ve önermelerin neden ve
niçinler üzerinde durularak kavramların anlamları ile birlikte öğrenilmesini
sağlamaktır. Bunun gerçekleştirilebilmesi için kavramların öğretilmesinde
aşağıdaki adımlar takip edilecektir.
1) Önermenin sözel ifadesinin verilmesi,
2) Sözel olarak ifade edilen önermelere ait geometrik şeklin çizilmesi
3) Önermenin çizilen şekle göre matematiksel ifadesinin yazılması
v
vi
GEOMETRI NEDIR?
4) Bu matematiksel ifadenin yine matematiksel olarak ispatlanması
5) İspatlanan bu önermenin ilgili bütün kavramlar için geçerli olduğunun
görülmesi.
Hz.Mevlana ’Ne kadar bilirsen bil, söylediklerin karşındakinin anlayabildiği kadardır’ derken özellikle biz öğretmenler için bilmenin gerek şart
olduğu ancak yeterli olmağını, bilginin karşımızdakine aktarılmasının da önemini vurgulamıştır.
Gösterilen tüm özene kaşın kitapta yazım hataları ve matematiksel hatalar bulunabilir. Bu konuda hertürlü eleştiri ve önerisi olan herkese saygı ile
karşılarım. Öğrencilerime faydalı olması dileklerimle ...
Doç.Dr.Recep ASLANER
Malatya, 2007
BÖLÜM 1
GEOMETRİK KAVRAMLAR
Tanımsız Kavramlar, Teorem, İspat ve Aksiyom.
Bir konuyla ilgili özel ve belirli bir anlamı olan sözcüklere terim denir. Bir
şeyin nitelikleri hakkındaki genel ifadelere ise kavram denir. Anlamı görsel
veya sezgisel olarak bilinen, tanımlamaya gerek duyulmayan kavramlara tanımsız kavram denir. Mesela nokta, doğru, küme vb gibi kavramlar birer tanısız
kavramdır. Bu kavramların anlamları tanımlanmış terimler yardımıyla açıklanabilir. Mesela, nokta sivri uçlu bir kalemin kağıt üzerinde veya tebeşirin
tahtada braktığı iz nokta hakkında bir fikir verir fakat bu açıklama matematiksel bir tanım değildir. Doğru yada yanlış bir hüküm bildiren ifadelere
önerme denir. Önermeler p, q, r gibi küçük harflerle gösterilir. Doğruluğu
hemen anlaşılamayan, ispat gerektiren önermelere teorem denir. p ve q birer
önerme olmak üzere p ⇒ q biçiminde ifade edilen şartlı önermeler birer teo-
remdir. Bu şartlı önerme ′ p ise q ′ veya ′ p gerektirir q ′ diye okunur. Bazen bir
teorem p ⇔ q biçiminde de ifade edilir. Böyle teoremlere çift taraflı teoremler
denir. p ⇒ q bileşik önermesinde p önermesine hipotez q önermesine hüküm
adı vrilir. Bir teoremin hipotezi doğru iken hükmünün de doğru olduğunun
gösterilmesine, o teoremin ispatı denir. İspatına gerek duyulmadan doğruluğu anlaşılan önermelere aksiyom denir.
Her geometrinin temel aksiyomları vardır. Öklid çalışmaların tutarlı bir
bütün olmasını sağlamak için, apaçık gerçekler olarak düşünülen beş aksiyom ortaya koyar ve diğer bütün önermeleri (teoremleri) bu aksiyomlardan
çıkarır. Bunlar;
1) İki noktadan bir ve yalnız bir doğru geçer.
2) Bir doğru parçası iki yöne sınırsız bir şekilde uzatılabilir.
1
2
1. GEOMETRİK KAVRAMLAR
3) Merkezi ve üzerinde bir noktası verilen çember çizilebilir.
4) Bütün dik açılar eşittir.
5) Bir doğruya dışındaki bir noktadan bir ve yalnız bir paralel çizilebilir.
1. NOKTA, DOĞRU, DOĞRU PARÇASI VE IŞIN
Nokta, tanımsız bir kavramdır. Noktalar alfabenin büyük harfleri ile
adlandırılır (•A), A noktası gibi.
Bir kalemin sivri ucu kağıt üzerinde gezdirildiğinde meydana gelen geometrik şekil bir noktalar kümesi olup bu şekle çizgi denir.
eğri çizgi
kırık çizgi
düz çizgi
Şekil 1. Çizgi
Geometride çizgiler kalınlığı olmayan yalnız uzunluk olarak ele alınan tek
boyutlu kavramlardır. Başlangıç ve bitiş noktaları belli olmayan (sonsuzda
kabul edilen ) düz çizgilere doğru denir. doğrular d, k, l, m, ... gibi küçük
d
Şekil 2. Doğru
harflerle gösterilir.
Farklı iki noktası A ve B olan doğru AB doğrusu diye ifade edilir.
d
A
B
Şekil 3. İki noktası belli olan doğru
Bir doğrunun en az iki farklı noktası vardır. Bir doğru üzerinde ikiden
daha fazla nokta alınırsa bu noktalara doğrudaş (doğrusal) noktalar denir.
1. NOKTA, DOĞRU, DOĞRU PARÇASI VE IŞIN
3
d
A
B
C
D
Şekil 4. Doğrudaş noktalar
Şekle göre
* d = AB doğrusu,
* A, B, C ∈ d olduğundan A, B, C noktaları doğrudaştır
* B noktası A ile C arasındadır,
* D ∈ d olduğundan A, B, D noktaları doğrudaş değildir.
Aksiyom 1.1. Farklı iki nokta bir tek doğru belirtir.
Tanım 1.1. Bir doğrunun A ve B gibi farklı iki noktası ve bu noktalar
arasındaki noktaların kümesine doğru parçası denir ve [AB] ile gösterilir.
A
B
d
[AB]
o
o (AB)
Şekil 5. Doğru parçası
A ve B noktalarına AB doğru parçasının uç noktaları, uç noktaları dışındaki noktalara da iç noktaları denir. İç noktaların kümesi (AB) ile gösterilir.
Tanım 1.2. Bir doğru üzerindeki bir A noktası ile bu noktanın aynı
tarafında bulunan noktaların kümesine, başlangıç noktası A olan bir ışın
denir ve [AX ile gösterilir.
Aynı doğrultuda fakat zıt yöndeki ışınlara zıt ışınlar denir.
C
A
B
4
1. GEOMETRİK KAVRAMLAR
A
X
A
X
d
[AX
Şekil 6. Işın
[AB ve [AC ışınları zıt ışınlardır.
Tanım 1.3. Bir [AB] doğru parçasının uzunluğuna, A ve B noktaları
arasındaki uzaklık denir ve |AB| ile gösterilir.
Uzunlukları eşit olan doğru parçalarına eş tir denir ve bu durum (∼
=)
sembolü ile gösterilir. [AB] ve [CD] iki doğru parçası olmak üzre;
|AB| = |CD| ⇔ [AB] ∼
= [CD]
Aksiyom 1.2. Her doğru parçası kendisine eştir.
’Uzayda farklı iki noktadan bir doğru geçer’ aksiyomuna göre O ve A
farklı iki nokta olmak üzere bu iki noktadan geçen doğruyu d ile gösterelim
P’
A
O
−x − ← 0 → + 1
P
x
d
R
Şekil 7. Sayı doğrusu
O ∈ d noktasına karşılık 0 ∈ R sayısını,
A ∈ d noktasına karşılık 1 ∈ R sayısını alalım ve |OA| = 1 birim diyelim.
0 dan itibaren 1 in bulunduğu tarafa pozitif (+) yön, diğer tarafa negatif (-)
yön olarak alırsak ∀x ∈ R sayısı, d doğrusu üzerinde O noktasına uzaklığı x
kadar olan bir P noktasına karşılık gelir, burada
x > 0 olması, P noktasının d nin (+) yölü parçasında,
x < 0 olması ise P noktası d nin (-) yönlü parçasında olması anlamındadır.
Böylece elde edilen
′
∀x ∈ R
için |OP | = x olacak şekilde bir tek P ∈ d vardır′
2. DÜZLEM VE İLGİLİ AKSİYOMLAR
5
önermesine Geometrinin Temel İlkesi, d doğrusuna da sayı doğrusu denir.
Eğer bir sayı doğrusu üzerindeki A noktasına karşılık gelen reel sayı a ise
a sayısına A noktasının koordinatı denir ve bu durum A(a) ile gösterilir.
Tanım 1.4. Bir d doğrunun üç noktası A, B ve C için
|AB| + |BC| = |AC|
ise B noktası A ile C arasındadır denir ve bu durum (ABC) ∈ d ile gösterilir.
Aksiyom 1.3. Farklı ve doğrudaş üç noktadan yalnız biri, diğer ikisinin
arasındadır.
Eğer (ABC) ∈ d ve |AB|=|BC| ise B noktasına [AC] doğru parçasının
a+c
dir.
orta noktası denir, orta noktanın koordinatı b =
2
2. DÜZLEM ve İLGİLİ AKSİYOMLAR
Nasıl ki bir doğru noktalardan oluşuyorsa bir düzlem de üzerinde bulunan
nokta ve doğrulardan oluşur. Bir doğruyu tanımak için en az iki noktaya
ihtiyaç olduğu gibi bir düzlemi tanımak için de en az bir doğru ve bu doğru
üzerinde olmayan bir noktaya ihtiyaç vardır. Diğer bir ifade ile bir düzlemi
tanımak için doğrudaş olmayan en az üç noktaya ihtiyaç vardır. Düzlemde,
en ve boy olmak üzere iki boyut vardır. Düzlem geometrik olarak bir paralel
kenarla gösterilir ve sol alt köşesine yazılan D, E, veya P gibi büyük harflerle
ifade edilir.
C
A
B
D
Tanım 1.5. Bir noktalar kümesinin tüm noktaları, bir doğruya ait ise
bu noktalara doğrusal, bir düzleme ait ise bu noktalara düzlemsel noktalar
denir.
6
1. GEOMETRİK KAVRAMLAR
Örnek 2.1. Aşağıdaki şekilde
C
A
B D
E
A,B,D noktaları doğrudaş, A,C,D noktaları düzlemseldir.
Böylece doğru ve düzlemle ilgili aşağıdaki aksiyomları ifade edebiliriz:
Aksiyom 1.4. Her hangi üç noktadan en az bir düzlem geçer.
Aksiyom 1.5. Doğrusal olmayan üç noktadan bir ve yalnız bir düzlem
geçer.
Aksiyom 1.6. Farklı iki nokta bir düzlemin elemanı ise bu iki noktadan
geçen doğru, o düzlemin içindedir.
Aksiyom 1.7. Düzlemin doğrusal olmayan en az üç noktası vardır.
Teorem 1.1. Bir düzlemde yatan farklı iki doğrunun en fazla bir ortak
noktası vardır.
İspat: d1 ve d2 bir D düzleminde yatan farklı iki doğru ve
T
d1 d2 = {A, B} olsun. Bu durumda Aksiyon 1.1 gereğince
AB = d = d1 = d2 olmalıdır.
Halbuki d1 6= d2 ⇒ A = B dir, yani d1
T
d2 = {A}.
d1
d
d2 A
B
D
Bu teoremden aşağıdaki sonuçları çıkarabiliriz.
2. DÜZLEM VE İLGİLİ AKSİYOMLAR
7
Sonuç 1.1. Aynı düzlemde yatan iki doğru için birden fazla ortak nokta
varsa bu doğrular çakışıktır, yani aynı doğruyu gösterirler.
Sonuç 1.2. Aynı düzlemde yatan farklı iki doğru için ya birtek ortak
nokta vardır ya da hiç ortak noktaları yoktur. Ortak noktaları olmayan
doğrulara paralel doğrular denir.
Sonuç 1.3. Aynı düzlemde yatmayan ve kesişmeyen doğrulara aykırı
doğrular denir.
Aksiyom 1.8. Düzlemde bir doğru ve bu doğru üzerinde bulunmayan bir
nokta verildiğinde, verilen noktadan geçen ve verilen doğruya paralel olan bir
tek doğru vardır.
d’
C
d
D
Teorem 1.2. Düzlemde paralel iki doğrudan biriyle kesişen başka bir
doğru, diğeriyle de kesişir.
İspat: d1 ve d2 paralel iki doğru ve k aynı düzlemde k ∩ d1 = {A} olan
başka bir doğru olsun. Kabul edelimki k ∩ d2 = ⊘ dir. Bu durumda Aksiyom
2.1 gereğince k//d2 ⇐⇒ k = d1 bu ise k 6= d1 önermesi ile çelişir. O halde
k 6= d1 ise k ∩ d2 6= ⊘ ⇔ k ∩ d2 = {B} olacak şekilde bir B noktası vardır.
A
B
D
k
d1
d2
8
1. GEOMETRİK KAVRAMLAR
Teorem 1.3. Bir düzlemde aynı doğruya papalel olan iki doğru birbirine
paraleldir.
Sonuç 1.4. Bir düzlemde, paralel iki doğrudan birine paralel olan bir
doğru, diğerine de paraleldir.
d, d′ doğruları ve D, D′ düzlemleri verildiğinde aşağıdaki önermeler doğrudur.
1) d ∩ D = ⊘ ⇒ d//D.
2) d ∩ D = {A}
3) d ∩ D = {A, B} ⇒ d ⊂ D
4) D ∩ D′ = ⊘ ⇒ D//D′
5) D ∩ D′ = d
6) D ∩ D′ = {d, d′ } ⇒ D = D′
BÖLÜM 2
AÇILAR
1. AÇILARLA İLGİLİ GENEL KAVRAMLAR
Tanım 2.1. Başlangıç noktaları ortak olan iki ışının birleşim kümesine
açı; açıyı oluşturan ışınların her birine, açının kenarları (veya kolları) ve bu
iki ışının ortak olan başlangıç noktasına da açının köşesi denir.
B
O
A
Şekil 1. Açı
ˆ
ˆ veya kısaca Ô ile
kenarları [OA ve [OB ışınları olan açı AOB,
BOA
gösterilir. ’kesişen iki doğru bir düzlem belirtir’ aksiyomuna göre açı da düzlemsel bir kavramdır. Her bir geometrik şekil gibi açılarda içinde bulunduğu
düzlemi üç ayrık bölgeye ayırır.
1) Açıyı oluşturan noktalar kümesi, Ô = [OA ∪ [OB
2) Açının iç bölgesi, açının kolları arasında kalan noktalar kümesi
3) Açının dış bölgesi.
Tanım 2.2. Bir çemberin çevresi 360 eşit parçaya bölünerek elde edilen
her bir parçanın uzunluğuna 1 derece denir ve 1o ile gösterilir. Köşesi bir
birim çemberin merkezi olan bir açının kolları arasında kalan yay uzunluğuna
da o açının radyan cinsinden ölçüsü denir.
9
10
2. AÇILAR
B
A
π
ˆ
0 ≤ α ≤ π(180o ) olmak üzere m(AOB)
= α(= 45o = )
4
ölçüsü 0 < α < 90o olan açılara dar açı, ölçüsü α = 90o olan açılara dik
açı ve ölçüsü 90o < α < 180o olan açılara geniş açı denir.
Tanım 2.3. Ölçüleri eşit olan açılara eş açılar denir. Verilen bir açıyı
iki eş parçaya ayıran ışına o açının açıortayı denir.
X
H2
P
O
H1
Şekil 2. Açıortayı
Tanım 2.4. Bir d doğrusu ve bu doğru üzerinde olmayan bir A noktası
verildiğinde, A noktasından d doğrusuna inilen dik doğru parçasının uzunluğuna A noktasının d doğrusuna uzaklığı denir. A noktasının d doğrusuna
uzaklığı l(A, d) = |AH|, H ∈ d ile gösterilir.
A
l
d
H
1. AÇILARLA İLGİLİ GENEL KAVRAMLAR
11
Sonuç 2.1. Bir açının açıortayı üzerindeki her noktanın açının kenarlarına
olan uzaklığı eşittir.
[OX, Ô açının açıortayı ise, |P H1 | = |P H2 |
Tanım 2.5. Köşeleri ve birer kenarları ortak olan iki açıya komşu açılar
denir.
C
B
O
A
Şekil 3. Komşu açılar
ˆ ve BOC
ˆ açıları komşu açılardır.
AOB
Tanım 2.6. Birinin kenarları, diğerinin kenarlarının ters ışınları olan
iki açıya ters açılar denir.
D
C
B
O
A
Şekil 4. Ters açılar
Aksiyom 2.1. Ters açılar eştir.
Saat yönündeki açıya negatif yönlü açı, saatin ters yönündeki açıya da
ˆ açısı (+) pozitif yönlü, COD
ˆ açısı (-) negatif
pozitif yönlü açı denir. AOB
yönlü açıdır.
12
2. AÇILAR
Tanım 2.7. Ölçüleri toplamı 90o olan iki açıya tümler (veya dikler) açılar
denir. Tümler iki açı aynı zamanda komşu açılar ise bunlara komşu tümler
açılar denir.
Tanım 2.8. Ölçüleri toplamı 180o olan iki açıya bütünler açılar denir.
Bütünler iki açı aynı zamanda komşu açılar ise bunlara komşu bütünler açılar
denir.
Tanım 2.9. Ölçüsü 180o olan açıya doğru açı, 360o olan açıya tam açı
denir.
Örnek 1.1. Bütünler iki açının ölçüleri farkı 72o ise, bu açıların her
birinin ölçüsü nedir?
Örnek 1.2. Bütünler iki açıdan birinin ölçüsü diğerinin ölçüsünün iki
katında 15o eksiktir. Bu açıların ölçüleri nedir?
2. PARALEL İKİ DOĞRUNUN BİR KESENLE YAPTIĞI
AÇILAR
d1 //d2 ve k doğruları aşağıdaki şekildeki gibi verilmiş olsun.
k
2
3
6
7
5
8
1
4
d1
d2
Şekil 5
Tanım 2.10. d1 ile d2 doğruları arasında kalan açılara iç açılar denir. 3,
4, 5 ve 6 numaralı açılar iç açılardır.
Tanım 2.11. d1 ile d2 doğruları arasında olmayan açılara dış açılar denir.
1, 2, 7 ve 8 numaralı açılar dış açılardır.
2. PARALEL İKİ DOĞRUNUN BİR KESENLE YAPTIĞI AÇILAR
13
Tanım 2.12. k doğrusunun farklı taraflarında kalan köşeleri farklı iç açı
çiftlerine iç ters açılar denir. (3, 5) ve (4, 6) açı çiftleri iç ters açılardır.
Tanım 2.13. k doğrusunun farklı taraflarında kalan köşeleri farklı dış açı
çiftlerine dış ters açılar denir. (1, 7) ve (2, 8) açı çiftleri dış ters açılardır.
Tanım 2.14. k doğrusunun aynı taraflarında kalan köşeleri farklı biri iç
açı, diğeri dış açı olan açı çiftlerine yöndeş açılar denir.
(1, 5), (4, 8), (2, 6) ve (3, 7) açı çiftleri yöndeş açılardır.
Aksiyom 2.2. Yöndeş açılar, iç ters açılar ve dış ters açılar eştir.
Bu aksiyomlardan aşağıdaki sonuçları çıkarabiliriz.
Sonuç 2.2. Paralel iki doğrudan birine dik olan başka bir doğru diğerine
de diktir.
dir.
İspat: Bu sonucun matematiksel ifadesi, d1 //d2 ve k ⊥ d1 ⇒ k ⊥ d2
k
.
1
d1
2
d2
Şekil 6
d1 //d2 ve k ⊥ d1 ⇒ m(1) = 90o dir. 1 ve 2 numaralı açılar yöndeş açılar
ve yöndeş açılar eş açılar olduğundan ⇒ m(1) = m(2) = 90o ⇒ k ⊥ d2 dir.
Sonuç 2.3. Verilen iki doğru üçüncü bir doğruya dik ise, bu iki doğru
birine paraleldir.
14
2. AÇILAR
İspat: Bu sonucun matematiksel ifadesi,
d1 ⊥ k ve d2 ⊥ k ⇒ d1 //d2 dir...
problem:
B
P
A
C
d1
Q
D
d2
E
F
Şekil 7
d1 //d2
ˆ
m(ABC)
= 30o








ˆ
m(DEC)
= 140o 
ˆ
⇒ m(BCE)
=?
Çözüm: C noktasından d1 doğrusuna bir paralel doğru çizip üzerinde
iki nokta seçelim. Bu durumda 
ˆ ) = m(ABC)
ˆ
m(BCP
= 30o 
(iç ters açılar eştir)
ˆ ) = m(P CE)
ˆ
m(CEF
= 40o 
ˆ
ˆ ) + m(P CE)
ˆ
⇒ m(BCE)
= m(BCP
= 30o + 40o = 70o bulunur.
3. KENARLARI PARALEL OLAN AÇI ÇİFTLERİ
Bu durumda üç ihtimal vardır.
1) Kenarların aynı yönde paralel olması durumu:
Teorem 2.1. Kenarları aynı yönde paralel olan açılar eştir.

[BA//[DC 
⇒ B̂ ∼
yani
= D̂

[BC//[DE
İspat: Yöndeş açıların eşlğinden B̂ ∼
= Ĉ ∼
= D̂ ⇒ B̂ ∼
= D̂
2) Kenarların ters yönde paralel olması durumu:
Teorem 2.2. Kenarları ters yönde paralel olan açılar eştir.
3. KENARLARI PARALEL OLAN AÇI ÇİFTLERİ
15
A
C
B
D
E
Şekil 8
A
K
D
B
E
C
F
Şekil 9

[BA//[EF 
⇒ B̂ ∼
= Ê

[BC//[ED
İspat: EF ∩ [BC = K diyelim. Bu durumda,

ˆ
B̂ ∼
(iç ters açılar ) 
= BKE
⇒ B̂ ∼
= Ê
ˆ ∼
BKE
= Ê (yöndeş açılar ) 
3) Birer kenarların aynı yönde, diğer kenarları ters yönde paralel olası
durumu:
Teorem 2.3. Bir düzlemde birer kenarları aynı yönde, diğer kenarları
ters yönde paralel olan iki açı bütünlerdir.

[BA//[EF 
⇒ m(B̂) + m(Ê) = 180o
[BC//[ED 
16
2. AÇILAR
A
F
K
B
D
G
C
E
Şekil 10
İspat:[BC ∩ [EF = K diyelim ve E noktasından [BC ışınına bir paralel
çizip üzerinde bir G noktası seçelim. Bu durumda,
ˆ ∼
ˆ yöndeş açılar
B̂ ∼
= F KC
= F EG
ˆ
m(Ê) + m(F EG)
= m(Ê) + m(B̂) = 180o
4. KENARLARI BİRBİRİNE DİK OLAN AÇI ÇİFTLERİ
Teorem 2.4. Bir düzlemde kenarları karşılıklı olarak dik olan iki açı;
a) açılar dar açı ise eştir,
b) açılardan biri dar diğeri geniş açı ise bütünlerdir.
İspat: Öncelikle teoremin ifadesine uygun şekillerimizi çizelim.
G
A
F
B
C
D
E
Şekil 11
A noktasından [DE ve [DC ye birer paralel ışın çizelim ve üzerlerinde F
ve G noktalarını seçelim. Bu durumda
4. KENARLARI BİRBİRİNE DİK OLAN AÇI ÇİFTLERİ
17

[AF//[DE 
ˆ
ˆ
⇒ [AF ⊥ [AC ⇒ m(BAC)
= 90o − m(F AB)
... (1)
[DE ⊥ [AC 

[AG//[DB 
ˆ
ˆ
⇒ [AG ⊥ [AB ⇒ m(F AG)
= 90o − m(F AB)
... (2)
[DB ⊥ [AB 
ˆ
ˆ
ˆ
(1) ve (2) ⇒ m(BAC)
= m(F AG)
= m(EDC)
⇔ Â ∼
= D̂
b) açılardan biri dar diğeri geniş çı ise bütünlerdir.
L
C
K
D
B
A
Şekil 12

[BA//[DK 
ˆ ... (1)
⇒ B̂ ∼
= KDL
[BC ⊥ [DL 

[BA//[DK 
ˆ
⇒ [DA ⊥ [DK ⇒ m(ADK)
= 90o ... (2)

[BA ⊥ [DA

[BC//[DL 
ˆ
⇒ [DC ⊥ [DL ⇒ m(LDC)
= 90o ... (3)
[BC ⊥ [DC 
ˆ
ˆ
ˆ
ˆ
m(ADK)
+ m(KDL)
+ m(LDC)
+ m(CDA)
= 360O
(1),(2)ve (3)
⇒ 90o + m(B̂) + 90o + m(D̂) = 360o
⇔ m(B̂) + m(D̂) = 180o
Sonuç 2.4. Komşu bütünler iki açının açıortayları diktir.
ˆ ve BOC
ˆ komşu bütünler iki açı ve [OD ve [OE bu açıların
İspat: AOB
açıortayları olsun. Bu durumda;
18
2. AÇILAR
D
B
E
A
O
C
Şekil 13
1
ˆ
ˆ
m(DOB)
= m(AOB)
2
ve
1
ˆ
ˆ
m(BOE)
= m(BOC)
2
ˆ
ˆ
ˆ
m(DOE)
= m(DOB)
+ m(BOE)
1
ˆ
ˆ
=
[m(AOB)
+ m(BOC)]
2
1
180o
=
2
= 90o
⇒ [OD ⊥ [OE.
BÖLÜM 3
ÜÇGENLER
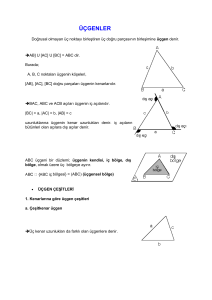
1. ÜÇGENLE İLGİLİ TEMEL KAVRANLAR
Doğrudaş olmayan üç noktanın bir düzlem, farklı iki noktanın bir doğru
parçası belirttiğini biliyoruz. A, B ve C doğrudaş olmayan üç nokta ve bu
noktalarla oluşturulan [AB], [BC] ve [CA] doğru parçalarının birleşim kümesine üçgen denir.
A
Â
c
b
B̂
B
Ĉ
a
C
Şekil 1. Üçgen
Bir üçgen, bu üçgeni oluşturan noktaların saatin ters yönünde sıralanarak
△
üzerine △ işareti konularak gösterilir. Buna göre yukarıdaki üçgen ABC ile
gösterilir ve
△
ABC = [AB] ∪ [BC] ∪ [CA]
△
1.1. Üçgenle İlgili Tanımlar: Bir ABC üçgeninde ;
1) A, B, C, noktalarına üçgenin köşeleri denir.
2) [AB], [BC] ve [CA] doğru parçalarına üçgenin kenarları denir.
Bir üçgende kenarlar karşı köşelerin küçük harfleriyle gösterilir. a, b, c gibi,
bu gösterim aynı zamanda kenar uzunluğu olarak alınır, yani a ile hem [BC]
kenarı hem de |BC| uzunluğu anlaşılır.
19
20
3. ÜÇGENLER
3) Uç noktaları ortak olan iki kenar arasında oluşan açılara üçgenin açıları
denir. Üçgende açılar köşe noktasının üzerine ∧ işreti konularak gösterilir.
Â, B̂, Ĉ gibi
Bunlara bir üçgenin temel elemanları denir ve her üçgende mevcuttur.
Üçgenler bu temel elemanlara göre sınıflandırılabilir.
1.2. Kenarlarına Göre Üçgen Çeşitleri.
1.2.1. Eşkenar üçgenler. Bütün kenar uzunlukları eşit olan üçgenlerdir.
Eşkenar üçgenlerin açıları da eştir.
1.2.2. İkizkenar üçgenler. İki kenar uzunluğu eşit olan üçgenlerdir. Uzunluğu farklı olan kenara taban denir. Bir ikiz kenar üçgende taban açıları eştir.
1.2.3. Çeşitkenar üçgenler. Bütün kenarları farklı uzunlukta olan üçgenlerdir. Çeşit kenar üçgenlerin açıları da farklıdır.
60o
60o
60o
eşkenar üçgen
ikizkenar üçgen
çeşit kenar üçgen
Şekil 2. Kenarlarına göre üçgen çeşitleri
1.3. Açılarına Göre Üçgen Çeşitleri. .
1.3.1. Dar açılı üçgenler. Her bir açısının ölçüsü 90o den küçük olan
üçgenlerdir.
1.3.2. Dik üçgenler. Açılarından birinin ölçüsü 90o olan üçgenlerdir.
1.3.3. Geniş açılı üçgenler. Açılarından birisi geniş açı olan üçgenlerdir.
1. ÜÇGENLE İLGİLİ TEMEL KAVRANLAR
dar açılı üçgen
Dik üçgen
21
geniş açılı üçgen
Şekil 3. Açılarına göre üçgen çeşitleri
1.4. Üçgende Yardımcı Elemanlar. .
Her üçgende var olan kenarortay, açıortay ve yükseklik kavramlarına üçgenin
yardımcı elemanları denir.
1.4.1. Kenarortay. Üçgenin bir kenarının orta noktasını o kenarı gören
köşe noktasına birleştiren doğru parçasına o kenara ait kenarortay denir. Her
üçgenin üç tane kenarortayı vardır. Bu kenarortaylar üçgenin iç bölgesindeki
bir noktada kesişirler. Bu noktaya üçgenin ağılık merkezi denir ve genellikle
G ile gösterilir.
A
F
B
G
E
D
C
Şekil 4. Kenarortaylar
△
ABC üçgeninde;
[AD], a-kenarına, [BE], b-kenarına ve [CF ], c-kenarına ait kenarortayları
göstermektedir.
22
3. ÜÇGENLER
1.4.2. Açıortay. Bir üçgende bir açıyı iki eşit parçaya ayıran ışının köşe
noktası ile karşı kenar arasında kalan kısmına üçgenin o açısına ait açıortay
denir. Bir üçgende üç tane açıortay vardır. Bu açıortaylar bir noktada
kesişir.
A
B
C
Şekil 5. Açıortaylar
1.4.3. Yükseklik. Üçgenin her hangi bir köşesinden karşı kenara inilen
dikmenin bu köşe ile karşı kenar (ya da uzantısı) arasında kalan doğru parçasının
uzunluğuna üçgenin o kenarına ait yükseklik denir ve h ile gösterilir.
A
ha
hc
B
hb
C
Şekil 6. Yükseklik
2. ÜÇGENDE AÇILAR
Teorem 3.1. Bir üçgenin iç-açılarının ölçüleri toplamı 180o dir,
△
yani bir ABC nin de m(Â) + m(B̂) + m(Ĉ) = 180o dir.
Ispat:
2. ÜÇGENDE AÇILAR
23
A
D
E
B
C
Şekil 7
Üçgenin A köşesinden [BC] kenarına bir paralel çizelim ve üzerinde iki
nokta D, E seçelim. Bu durumda;
∼
ˆ
DAB
= B̂
∼ Â
 =
∼
ˆ
CAE
= Ĉ


(iç ters açılar) 


(kendisi)



(iç ters açılar) 
ˆ
ˆ
⇒ m(DAB)
+ m(Â) + m(CAE)
= 180o = m(B̂) + m(Â) + m(Ĉ)
Örnek 2.1. Bir üçgenin iç açılarının ölçüleri sırsıyla 2, 3 ve 4 ile doğru
orantılı ise bu açıların ölçüleri nedir?
Çözüm: Bu açıların ölçülerini sırasıyla α, β ve γ diyelim. Bu durumda
β
γ
α
= = = k ∈ R ve α + β + γ = 180o
2
3
4
⇒ 2k + 3k + 4k = 180o = 9k ⇒ k = 20o
⇒ α = 2k = 40o , β = 3k = 60o ve γ = 4k = 80o bulunur.
△
Tanım 3.1. Bir ABC nin [BC] kenarını BC yönünde uzatarak üzerinde
ˆ açısına C köşesine ait dış
bir D noktası seçelim. Böylece elde edilen ACD
açı denir ve Ĉ ′ ile gösterilir. Â ve B̂ açılarına da Ĉ ′ açısına komşu olmayan
iç açılar denir.
Teorem 3.2. Üçgende bir dış açının ölçüsü, kendisine komşu olmayan
iki iç açının ölçüleri toplamına eşittir.
24
3. ÜÇGENLER
A
E
Ĉ ′
C
B
D
Şekil 8. Dış açı
yani ,
m(Ĉ ′ ) = m(Â + m(B̂)) dir.
İspat: şekilde C noktasından [BA] ya bir paralel çizip üzerinde bir E
noktası seçelim. Bu durumda;
ˆ ∼
DCE
= B̂ ( yöndeş açılar )
ˆ ∼
ECA
= Â (iç ters açılar)
ˆ
ˆ
m(Ĉ ′ ) = m(DCE)
+ m(ECA)
= m(Â) + m(B̂)
Sonuç 3.1. Bir üçgende bir dış açının ölçüsü, kendisine komşu olmayan
iki iç açının her birinden daha büyüktür.
2.1. Üçgende Kenarlar ile Açılar Arasındaki Bağıntılar.
Teorem 3.3. :
△
Bir ABC üçgeninde |AB| > |AC| ⇔ m(Ĉ) > m(B̂) dir.
İspat: |AB| > |AC| olsun. Bu durumda [AB] üzerinde
A
D
B
E
C
Şekil 9. Kenar-açı ilişkisi
2. ÜÇGENDE AÇILAR
25
|AD| = |AC| olacak şekilde bir D ∈ [AB] vardır. D ←→ C, [BC]//[DE]
olsun. Bu durumda
ˆ
ˆ
ˆ
m(ACB)
> m(ACD)
= m(ADC)
(ikiz kenar üçgende taban açılar)
ˆ
ˆ
m(ADC)
> m(ADE)
= m(B̂) (yöndeş açılar)
ˆ
⇒ m(ACB)
= m(Ĉ) > m(B̂)
Teorem 3.4. (Üçgen Eşitsizliği): Bir üçgende her hangi bir kenarın
uzunluğu, diğer iki kenarın uzunluklarının farkından büyük, toplamından
daima küçüktür.
△
yani bir ABC nin de daima |b − c| < a < b + c dir.
İspat:
D
b
A
c
b
a
B
C
Şekil 10. Üçgen eşitsizliği
~ doğrultusunda |AD| = |AC| şartını sağlayan bir D noktası alalım ve
BA
D ←→ C. Buna göre;
1) |BD| = |BA| + |AD| = c + b
ˆ
ˆ
ˆ
ˆ
2) m(BCD)
> m(ACD)
= m(ADC)
= m(BDC)
⇒ |BD| > |BC| ⇒ c + b > a ... (1)
Benzer düşünceyle a + b > c ve a + c > b olduğu gösterilebilir.
3) a + b > c ⇒ a > |c − b| > 0 ... (2)
O halde (1) ve (2) den |b − c| < a < b + c elde edilir.
26
3. ÜÇGENLER
3. ÜÇGENLERDE EŞLİK KAVRAMI
△
△
ABC ve DEF herhangi iki üçgen olmak üzere, ABC ←→ DEF ifade-
siyle, bu üçgenlerin elemanlarının karşılıklı olarak eşlendiği gösterilir. Her
hangi iki üçgenin elemanları arasında yapılan bir eşlemede, karşılıklı kenarları
ve karşılıklı açıları eş ise bu üçgenlere eş üçgenler denir ve bu durum (∼
=) sembolü ile gösterilir.
Buna göre bir ABC ←→ DEF eşlemesinde;

△
△
1) |AB| = |DE|, |BC| = |EF |, |CA| = |F D| 
⇒ ABC ∼
= DEF

2)
 ∼
B̂ ∼
Ĉ ∼
= D̂,
= Ê,
= F̂
Not: İki üçgenin köşe noktaları arasında P (3, 3) = 3! = 6 farklı eşleme
yapılabilir. Ancak bu altı eşlemeden yalnızca biri bir eşlik bağıntısıdır. Eğer
üçgenler eşkenar üçgenler ise bu durumda her bir eşleme bir eşlik bağıntısıdır.
Yukarıdaki eşlik tanımına bakıldığında, verilen iki üçgenin eş olabilmesi
için bu üçgenlerin karşılıklı altı elemanın eş olması gerek şart olarak görülmektedir, fakat bu altı elamandan bazılarının gerçekleşmesi bazılarının gerçekleştiğini garantiler.
Bunları birer aksiyom olarak ifade edebiliriz.
3.1. Üçgenlerde Eşlik Aksiyomları.
Aksiyom 3.1. (K.A.K) Eşlik Aksiyomu Her hangi iki üçgen arasında
yapılan bir eşlemede, karşılıklı ikişer kenarları ve bu kenarlar arasında oluşan
açıları eş ise bu üçgenler eştir.
Yani bir ABC ←→ DEF eşlemesinde;


[AB] ∼
= [DE] 


△
△
∼
⇒ ABC ∼
= DEF dir.
B̂ = Ê



∼
[BC] = [EF ] 
3. ÜÇGENLERDE EŞLİK KAVRAMI
A
B
27
D
C
E
F
Şekil 11. Kenar Açı Kenar eşliği
Aksiyom 3.2. ((A.K.A) Eşlik Aksiyomu) Her hangi iki üçgen arasında
yapılan bir eşlemede, karşılıklı ikişer açıları ve bu açıların ortak olan kenarları eş ise bu üçgenler eştir.
A
B
K
D
C
E
L
F
Şekil 12. Açı Kenar Açı eşliği
Yani bir ABC ←→ DEF eşlemesinde;
B̂ ∼
= Ê
[BC] ∼
= [EF ]
Ĉ ∼
= F̂









△
△
⇒ ABC ∼
= DEF dir.
Bu aksiyomlardan aşağıdaki sonucu verebiliriz.
Sonuç 3.2. Eş üçgenlerde karşılıklı açıortaylarda eştir.

△
△

∼

ABC = DEF


∼
Yani
[AK], Â açısının açıortayı  ⇒ [AK] = [DL] dir.


[DL], D̂ açısının açıortayı 
28
3. ÜÇGENLER
△
△
İspat: ABC ∼
= DEF olsun. Bu durumda;
1
1
ˆ ∼
ˆ
1) Â ∼
= EDL
= D̂ ⇒ m(Â) = m(D̂) ⇒ m(Â) = m(D̂) ⇒ BAK
2
2
2) [AB] ∼
= [DE] ve
3)
B̂ ∼
= Ê
△
△
(A.K.A) eşlik aksiyomu gereğince ABK ∼
= DEL ⇒ [AK] ∼
= [DL]
Teorem 3.5. Tabanları ortak olan iki ikizkenar üçgenin, tepe noktalarını
birleştiren doğru parçası tepe açılarının açıortayıdır.
İspat:
A
12
B
1
1
2
C
2
12
D
Şekil 13
ikiz kenar üçgenlerde taban açılar eş olduğundan,


m(B1 ) = m(C1 ) 
B̂1 ∼
= Cˆ1 
ˆ
ˆ
⇒
⇒ m(ABD)
= m(ACD)


∼
ˆ
B̂2 = C2
m(B2 ) = m(C2 )






 Â ∼
1 = Â2
ˆ
ˆ
K.A.K ⇒ ABD ∼
= ACD ⇒
m(ABD)
= m(ACD)

 D̂1 ∼

= D̂2


|BD| = |CD|
|AB| = |AC|
△
△
elde edilir. Bu ise [AD] nin tepe açılarının açıortay olması demektir.
Teorem 3.6. Bir üçgenin bir kenarının orta noktasından başka bir kenara çizilen paralel doğru üçüncü kenarı ortalar.
3. ÜÇGENLERDE EŞLİK KAVRAMI
29
A
F
B
E
D
C
Şekil 14

|AE| = |EC| 
1
⇒ |BD| = |DC| = |BC|
2
[ED]//[AB] 
İspat: [EF ]//[BC] olsun. Buna göre;


ˆ 

 ∼
= DEC


 |EF | = |CD|
△
△
= ECD ⇒
[AE] ∼
= [EC]  ⇒ AEF ∼
 |AF | = |ED|



∼
ˆ
AEF = Ĉ



∼
ˆ
ˆ
BF D = F DE 

 |BF | = |ED| = |CD|

△
△
∼
∼
⇒
BF
D
EDF
⇒
=
[F D] = [DF ]
 |BD| = |EF | = |CD|




∼
ˆ
ˆ
F DB
DF
E
=
1
⇒ |BC| = BD| + |DC| ⇒ |BD| = |DC| = |BC| elde edilir.
2
Sonuç 3.3. Bir üçgende iki kenarın orta noktalarını birleştiren doğru
parçası, üçüncü kenara paraleldir ve uzunluğu, üçüncü kenarın uzunluğunun
yarısına eşittir,

|AE| = |EC| 
1
yani, bir ABC nin de
⇒ |DE| = |AB|.

2
|BD| = |DC|
△
Teorem 3.7. (K.K.K.) Eşlik Teoremi İki üçgen arasında yapılan bir
eşlemede karşılıklı kenarlar eş ise bu üçgenler eştir.
(K.K.K) eşlik teoremi denir.
yani bir ABC ←→ DEF eşlemesinde;
Bu teoreme kısaca
30
3. ÜÇGENLER

∼

[AB] = [DE] 


△
△
= DEF dir.
[BC] ∼
= [EF ]  ⇒ ABC ∼


[CA] ∼
= [F D] 
İspat: Bu teoremin ispatını (∼
=) bağıntısının geçişme özelliğini kullanarak yapabiliriz, yani verilen her iki üçgene de eş olan üçüncü bir üçgen
oluşturarak bu iki üçgenin eş olduğunun gösterebiliriz.
A
D
1 2
B
C
E
F
1 2
K
X
Şekil 15. K.K.K. eşliği
△
ˆ ∼
ABC nin B köşesinde CBX
= Ê olacak şekilde bir [BX ışını ve üzerinde
|BK| = |ED| olacak şekilde bir K 
noktası seçip K ←→ C. Bu durumda,

|KB| = |ED| 


△
△
∼
(K.A.K) ⇒ KBC ∼
= DEF ... (1)
B̂ = Ê



|BC| = |EF | 
K ←→ A. Bu durumda,
△
|KB| = |DE| = |AB| ⇒ BKA - ikiz kenar üçgen ⇒ m(K̂1 ) = m(Â1 )
△
|KC| = |DF | = |AC| ⇒ CAK - ikiz kenar üçgen ⇒ m(K̂2 ) = m(Â2 )
⇒ m(K̂) = m(Â) ⇒ K̂ ∼
= Â


|KB| = |AB| 


△
△
∼
(K.A.K) ⇒ KBC ∼
= ABC ... (2)
K̂ = Â



|KC| = |AC| 
△
△
(1) ve (2) ⇒ ABC ∼
= DEF
Bu teormeden aşağıdaki sonucu çıkarabiliriz.
4. ÜÇGENLERDE BENZERLİK KAVRAMI
31
Sonuç 3.4. Bir ikiz kenar üçgende tabana ait kenar ortay, aynı zamanda
hem yükseklik hem de açıortay dır.
△
Yani bir ABC nin de



 [AD] ⊥ |BC| (yükseklik)
|AB| = |AC| (ikiz kenar)
⇒
 Â1 ∼
|BD| = |DC| (D, orta nokta) 
= Â2 (açıortay)
△
İspat: ABC nin de
|AB| = |AC| (ikiz kenar)
|BD| = |DC| (D, orta nokta)
|AD| = |AD| (kendisi)
Buna göre,









△
△
(K.K.K) ⇒ ABD ∼
= ACD
1) D̂1 ∼
= D̂2 ve m(D̂1 ) + m(D̂2 ) = 180o
⇒ [AD] ⊥ [BC] ⇒ [AD]- tabana ait yükseklik,
2) Â1 ∼
= Â2 ⇒ [AD], Â- nın açıortayıdır.
4. ÜÇGENLERDE BENZERLİK KAVRAMI
İki üçgen arasında yapılan bir eşlemede, karşılıklı açılar eş ve karşılıklı
kenar uzunlukları orantılı ise bu eşlemeye benzerlik eşlemsi, üçgenlere de
benzer üçgenler denir, bu durum (∼) sembolü ile gösterilir. Buna göre bir
ABC ←→ DEF eşlemesinde,


∼
∼
∼

 = D̂, B̂ = Ê, Ĉ = F̂
△
△
⇔ ABC ∼ DEF
|AB|
|BC|
|AC|
=
=
=k 

|DE|
|EF |
|DF |
Buradaki k sayısına benzerlik oranı denir. k = 1 ise eşlik,
k 6= 1 ise benzerlik söz konusudur, yani benzerlik eşlikten daha geniş bir
kavramdır.
32
3. ÜÇGENLER
Aksiyom 3.3. (K.A.K.) Benzerlik Aksiyomu İki üçgen arasında yapılan
bir eşlemede, karşılıklı iki kenar uzunlukları orantılı ve bu kenarların oluşturduğu açılar eş ise üçgenler benzerdir. Buna kısaca (K.A.K) benzerlik aksiyomu denir,
yani ABC ←→ DEF eşlemesinde,
A
D
∼
B
∼
K
C
E
≈
L
≈
F
Şekil 16. K.A.K.benzerliği

|BC| 
|AB|

△
△
=
|DE|
|EF |
⇔ ABC ∼ DEF dir.


B̂ ∼
= Ê
Bu aksiyomdan aşağıdaki sonuç çıkarılır.
Sonuç 3.5. İki üçgen benzer ise, karşılıklı kenarortay uzunluklarının
oranı benzerlik oranına eşittir.
△
△
yani ABC ∼ DEF ve benzerlik oranı k olmak üzere,

|BK| = |KC| 
|AK|
= k dır.
⇒

|DL|
|DL| = |LF |
△
△
İspat:ABC ∼ DEF ve benzerlik oranı k olsun. Bu durumda,
|AB|
=k
2) B̂ ∼
= Ê
|DE|
1
|BC|
|BK|
|BC|
= k ⇒ 21
=k
=k⇒
3)
|EF |
|EL|
2 |EF |
1)
△
△
⇒ ABK ∼ DEL ⇒
|AB|
|AK|
|AK|
=
=k⇒
=k
|DL|
|DE|
|DL|
4. ÜÇGENLERDE BENZERLİK KAVRAMI
33
△
Tanım 3.2. Bir ABC nin de herhagi bir kenar uzunluğu ile bu kenara
△
ait yüksekliğin çarpımının yarısına bu üçgenin alanı denir ve s(ABC) ile
gösterilir.
Bu tanımdan aşağıdaki sonuç elde edilir.
Sonuç 3.6. Yükseklikleri eşit olan iki üçgenin alanları oranı, yüksekliklerin ait olduğgu kenarların uzunlukları oranına eşittir.
△
yani şekil (*)’a göre [AH] ∼
=
[DH ′ ]
⇒
s(ABC)
△
s(DEF )
=
|BC|
dir.
|EF |
Teorem 3.8. (Temel Orantı Teoremi) Bir üçgenin bir kenarına paralel
olan ve diğer iki kenarı kesen bir doğru bu kenarları uzunlukları orantılı doğru
parçalarına ayırır,
A
H
H’
D
E
B
k
C
Şekil 17. T.O.T teoremi
△
yani bir ABC ni için k//[BC], k ∩ [AB] = D ve k ∩ [AC] = E ise,
µ
¶
|AE|
|AE|
|AD|
|AD|
=
=
veya
(4.1)
|BD|
|EC|
|AB|
|AC|
İspat: B ←→ E , bu durumda;
△
△
|EH|, ADE ve DBE üçgenlerinin ortak olan yüksekliği olduğundan
△
(4.2)
s(ADE)
△
s(DBE)
=
|AD|
|DB|
34
3. ÜÇGENLER
C ←→ D , bu durumda;
△
△
|DH ′ |, ADE ve EDC üçgenlerinin ortak olan yüksekliği olduğundan
△
s(ADE)
(4.3)
△
=
s(EDC)
△
|AE|
|EC|
△
[DE], DEB ve DEC üçgenlerinin ortak olan tabanı ve [DE]//[BC] olduğundan bu iki üçgen aynı yüksekliğe sahiptir, dolayısıyla alanları eşittir, yani
△
(4.4)
△
s(DEB) = s(DEC)
bu eşitliklerinden
|AD|
|AE|
=
elde edilir.
|DB|
|EC|
5. ÜÇGENLERDE AÇIORTAY TEOREMLERİ
Teorem 3.9. (İç Açıortay Teoremi) Bir üçgende, herhangi bir iç açıortayın karşı kenar üzerinde ayırdığı parçaların uzunlukları oranı, bu parçalara
bitişik kenarların uzunlukları oranına eşittir.
A
L
K
B
D
C
Şekil 18. İç açıortay teoremi
△
Yani bir ABC ninde  nın iç açıortayı [AD] ise,
|AB|
|BD|
=
dir.
|DC|
|AC|
△
İspat: ABC ninde  nın iç açıortayı [AD] olsun. Bu durumda;
|KD| = |DL| olup bir oranda pay ve paydanın aynı değerle çarpıl-
ması, oranın değerini değiştirmediğinden,
1
1
|AB||KD|
|BD|h
|AB|
s(ABD)
|BD|
= 21
= 21
=
=
|AC|
s(ADC)
|DC|
2 |AC||DL|
2 |DC|h
5. ÜÇGENLERDE AÇIORTAY TEOREMLERİ
35
Teorem 3.10. (Dış Açıortay Teoremi) Bir üçgende herhangi bir dış açıotayı karşı kenar doğrusunu kesiyorsa, bu doğru üzerinde ayırdığı parçaların
uzunlukları oranı, bu parçalara bitişik kenarların uzunlukları oranına eşittir.
A
B
D
C
E
Şekil 19. Dış açıortay teoremi
△
Yani bir ABC ninde A′ dış açısının açıortayı [AE] ise
|BE|
|AB|
=
dir.
|CE|
|AC|
Not: Eğer üçgen bir eşkenar üçgen ise, dış açıortayları karşı kenar doğrularına paralel olduğundan dış açıortayları karşı kenar doğrularını kesmez.
Bu iki teoremi birleştirerek aşağıdaki teorem elde edilir.
Teorem 3.11. (Açıortay Teoremi:) Bir üçgende herhangi bir köşedeki iç
ve dış açıortayın karşı kenar ve uzantısı üzerinde ayırdığı parçaların uzunlukları oranı, bu parçalara bitişik kenarların uzunlukları oranına eşittir.
△
Yani bir ABC ninde  iç açısının açıortayı [AD] ve Â′ dış açısının açıortayı [AE] ise
|BD|
|AB|
|BE|
=
=
|DC|
|AC|
|CE|
dir.
Örnek 5.1. şekil () da |DC| = 2cm ve |CE| = 10cm ise, |BD| = x kaç
cm dir?
36
3. ÜÇGENLER
6. ÜÇGENLERDE BENZERLİK TEOREMLERİ
Teorem 3.12. (A.A.A. Benzerlik Teoremi) İki üçgen arasında yapılan
bir eşlemede, karşılıklı açılar eş ise üçgenler benzerdir.
Bu teoreme kısaca (Açı Açı Açı)-benzerlik teoremi denir.
Yani, bir ABC ←→ DEF eşlemesinde,
△
△
 ∼
= D̂, B̂ ∼
= Ê, Ĉ ∼
= Ê ⇒ ABC ∼ DEF dir.
Ispat: ABC ←→ DEF eşlemesinde, Â ∼
= D̂, B̂ ∼
= Ê, Ĉ ∼
= Ê olsun.
Bu durumda |AB| ve |DE| kenar uzunlukları için iki ihtimal vardır.
1) |AB| = |DE| olması durumu. Bu durumda
 ∼
= D̂
|AB| = |DE|
Ĉ ∼
= Ê









△
△
△
△
(A.K.A.)ABC ∼
= DEF ⇒ ABC ∼ DEF
2) |AB| > |DE| (veya |AB| < |DE| de olabilir) olması durumu. Bu
durumda
D
A
E’
F’
E
B
F
C
Şekil 20. A.A.A Benzerliği
[AB]-kenarı üzerinde |AE ′ | = |DE| eşitliğini sağlayan bir E ′ noktası
vardır. Benzer düşünceyle,
[AC]-kenarı üzerinde |AF ′ | = |DF | eşitliğini sağlayan bir F ′ noktası seçe-
lim. Bu durumda,
6. ÜÇGENLERDE BENZERLİK TEOREMLERİ

′

|AE | = |DE| 


(K.A.K)
 ∼
= D̂



|AF ′ | = |DF | 
⇒ Ê ′ ∼
= Ê,
△
37
△
AE ′ F ′ ∼
= DEF
Fˆ′ ∼
= F̂ ⇒ [E ′ F ′ ]//[BC]
T.O.T den
△
△
△
△
△
|AF ′ |
|AE ′ |
=
⇒ ABC ∼ AE ′ F ′ ∼
= DEF ⇒ ABC ∼ DEF .
|AB|
|AC|
Sonuç 3.7. İki üçgen arasında yapılan bir eşlemede, karşılıklı ikişer
açıları eş ise üçgenler benzerdir.
△
△
Yani bir ABC ←→ DEF eşlemesinde, Â ∼
= D̂, B̂ ∼
= Ê ⇒ ABC ∼ DEF .
Teorem 3.13. (K.K.K. Benzerlik Teoremi) İki üçgen arasında yapılan
bir eşlemede, karşılıklı kenarlar orantılı ise üçgenler benzerdir.
Yani, bir ABC ←→ DEF eşlemesinde,
△
△
|BC|
|AC|
|AB|
=
=
⇒ ABC ∼ DEF ,
|DE|
|EF |
|DF |
(Â ∼
= D̂, B̂ ∼
= Ê, Ĉ ∼
= F̂ )
△
△
Ispat: Eğer k = 1 ise K.K.K. Eşlik Teoreminden ABC ∼
= DEF
△
△
⇒ ABC ∼ DEF
k 6= 1 ve k > 1 olsun. Bu durumda,
D
A
E′
F′
B
E
C
Şekil 21. K.K.K. benzerliği
|AB| > |DE| olup |DE| = |AE ′ |
eşitliğini sağlayan bir tek E ′ ∈ [AB] noktası ve
F
38
3. ÜÇGENLER
|AC| > |DF | olup |DF | = |AF ′ |
eşitliğini sağlayan bir tek F ′ ∈ [AC] noktası vardır,
|AC|
|AB|
|AC|
|AB|
=
eşitliğinden
=
yazılabilir ve  ∼
= Â olup
′
|DE|
|DF |
|AE |
|AF ′ |
K.A.K Benzerlik Aksiyomuna göre
△
△
|AB|
|BC|
=
ABC ∼ AE ′ F ′ ⇒ B̂ ∼
= Ê ′ ve
|E ′ F ′ |
|AE ′ |
|AE ′ |
|DE|
= |BC|
= |EF |
|AB|
|AB|

′

|AE | = |DE| 


′
′
(K.K.K. Eşlik Aksiyomu)
|E F | = |EF |



|AF ′ | = |DF | 



D̂ ∼
= Â


⇒
Ê ∼
= B̂ ⇒ Ê ∼
= Ê ′ ∼
= B̂



 F̂ ∼
= Ĉ ⇒ F̂ ∼
= Ĉ
= Fˆ′ ∼
⇒ |E ′ F ′ | = |BC|
△
△
AE ′ F ′ ∼
= DEF
Bu teoremden aşağıdaki sonuç verilebilir.
Sonuç 3.8. Benzer iki üçgenin çevre uzunluklarının oranı benzerlik oranına
eşittir.
7. DOĞRU PARÇALARININ UZUNLUKLARI ARASINDAKİ ORAN VE ORANTI
39
7. DOĞRU PARÇALARININ UZUNLUKLARI ARASINDAKİ
ORAN VE ORANTI
Teorem 3.14. (I.Tales Teoremi) Bir paralel doğru demeti her hangi iki
kesenle kesildiğinde, kesenler üzerinde oluşan doğru parçalarının uzunlukları
orantılıdır.
A
m
n
D
B
K
d1
E
C
d2
F
d3
Şekil 22. I.Tales Teoremi
Teoremin bu şekle göre ifadesi
d1 // d2 // d3
m ∩ (d1 , d2 , d3 ) = (A, B, C)








n ∩ (d1 , d2 , d3 ) = (D, E, F ) 
⇒
|AB|
|DE|
=
|BC|
|EF |
Ispat: A ←→ F ve [AF ] ∩ d2 = K diyelim.
Bu durumda d2 // d3 olduğundan T.O.T. ne göre,
|AB|
|AK|
|DE|
=
=
|BC|
|KF |
|EF |
⇒
|AB|
|DE|
=
|BC|
|EF |
Sonuç 3.9. Eğer burada |AB| = |BC| ise, yani paralel doğru demeti
her hangi bir kesen üzerinde eş parçalara ağrılıyor ise her kesen üzerinde eş
parçalara ayrılır.
|AB| = |BC| ⇒ |AK| = |KF | & |DE| = |EF | dir.
40
3. ÜÇGENLER
Teorem 3.15. (II.Tales Teoremi) Kesişen iki doğru, paralel iki oğru ile
kesildiğinde oluşan üçgenler benzerdir.
Bu ifadeyi karakterize eden iki farklı geometrik gösterim vardır.
d2
A
B
K
d1 D
C
k1
k2
(a)
Şekil 23. II.Tales Teoremi
△
(b)
△
k1 ∩ k2 = K ve d1 //d2 ⇒ AKB ∼ CKD.



 ∼
Ĉ
=


△
△
İspat: k1 ∩ k2 = {K} ve d1 //d2 ⇒ K̂ ∼
= K̂  ⇒ AKB ∼ CKD.


B̂ ∼
= D̂ 
Tanım 3.3. Bir [AB] ve bir C ∈ (AB) iç noktası verildiğinde,
|AC| = m ve |CB| = n ise,
A
m
n
B
C
C noktasına [AB] sını
m
oranında içten bölen nokta,
n
B noktasına [AC] sını
m+n
oranında dıştan bölen nokta, denir.
n
Soru: Acaba her hangi bir [AB] sı ve m > n ∈ R+ sayıları verildiğinde,
m
bu doğru parçasını
oranında içten ve dıştan bölen noktalar var mıdır?
n
Eğer varsa nasıl bulunur?
7. DOĞRU PARÇALARININ UZUNLUKLARI ARASINDAKİ ORAN VE ORANTI
41
Cevap: Yukarıdaki şartları sağlayan iki nokta her zaman vardır ve aşağıdaki şekilde bulunur.
Bir [AB] sı ve m > n ∈ R+ sayıları verilmiş olsun. Doğrultusu AB
doğrultusundan farklı olan bir [AX ışını çizip üzerinde
|AC| = m ve |CD| = |CE| = n eşitliklerini sağlayan C, D ve E noktalarını
belirleyelim.
X
E
m
D
C
n
n
A
B
K
L
Şekil 24
D, E ←→ B ve [DB]//[CL] ve [EB]//[CK] olacak şekilde elde edilen
K, L ∈ AB noktaları için
|AC|
m
m
|AK|
=
=
olup K noktası [AB] sını
oranında içten bölen,
|KB|
|CE|
n
n
|AC|
m
m
|AL|
=
=
olup L noktası [AB] sını
oranında dıştan bölen
|LB|
|CD|
n
n
nokta dır.
5
oranında içten ve
3
dıştan bölen noktalar C ve D ise, |AC|, |AD|, |BC| ve |BC| uzaklıklarını
Örnek 7.1. Uzunluğu 4 cm olan bir [AB] sını
hesaplayınız.
△
Teorem 3.16. (Menelaus Teoremi) Bir ABC nin kenarlarını veya uzantısını bir d doğrusu sırasıyla X, Y ve Z noktalarında kesiyor ise
Şekil 25
dir.
|XB| |Y C| |ZA|
.
.
=1
|XC| |Y A| |ZB|
42
3. ÜÇGENLER
A
C’
Y
Z
d
A’
B’
X
B
C
Şekil 25. Menelaus Teoremi
İspat: A, B ve C noktaları d doğrusu üzerinde olmadığından bu noktaların d üzerindeki dik izdüşüm noktalarına A′ , B ′ ve C ′ dersek
[AA′ ], [BB ′ ], [CC ′ ] ⊥ d ⇒ [AA′ ] // [BB ′ ] // [CC ′ ]
II.Tales Teoreminden
[AA′ ] // [BB ′ ]
⇒
|AA′ |
|ZA|
=
|ZB|
|BB ′ |
[AA′ ] // [CC ′ ]
⇒
|CC ′ |
|Y C|
=
|Y A|
|AA′ |
[AA′ ] // [CC ′ ]
⇒
|XB|
|BB ′ |
=
|XC|
|CC ′ |
bu üç eşitliği taraf tarafa çarparsak
△
|XB| |Y C| |ZA|
.
.
= 1 elde edilir.
|XC| |Y A| |ZB|
Örnek 7.2. G noktası bir ABC nin ağırlık merkezi ve [AD], [BC] ke2
|AG|
narına ait kenarortay ise
= olduğunu gösteriniz .
|AD|
3
7. DOĞRU PARÇALARININ UZUNLUKLARI ARASINDAKİ ORAN VE ORANTI
43
△
Teorem 3.17. (Seva Teoremi) Bir ABC ni düzleminde alınan bir O noktasını üçgenin köşe noktalarına birleştiren doğrular karşı kenarları sırasıyla
X, Y ve Z noktalarında keserse,
Y
A
A
Z
Y
O
X
B
C
B
C
X
O
Z
Şekil 26. Seva Teoremi
|BX| |CY | |AZ|
.
.
=1
|XC| |Y A| |ZB|
(7.5)
İspat:
△
BCZ ni ne AX kesenine göre Menelaus Teoremi uygulanırsa
|BX| |CO| |ZA|
.
.
=1
|XC| |OZ| |AB|
(7.6)
△
AZC ni ne BY kesenine göre Menelaus Teoremi uygulanırsa
|CY | |AB| |ZO|
.
.
=1
|Y A| |BZ| |OC|
(7.7)
5.4 ve 5.5 taraf tarafa çarpılırsa 5.3 elde edilir.
△
Örnek 7.3. Bir ABC ninde  sının açıortayı [AD] aynı zamanda [BC]
kenarına ait yükseklik, E ∈ [AB] olsun. F, [EC] nin orta noktası omak üzere,
|AC| = 14cm, |AE| = 6cm ⇒ |DE| kaç cm dir?
44
3. ÜÇGENLER
A
E
1
2
F
B
D
C
Şekil 27
Çözüm: Öncelikleverilenlere uygun olan şeklimizi çizelim.
m(Â1 ) = m(Â2 ) 
⇒ |BD| = |DC| ⇒ |AB| = |AC| = 14cm

m(D̂) = 90o
E ∈ [AB] ve |AE| = 6cm verilmiş,
|AB| = |AE| + |EB| = 6 + |EB| = 14cm ⇒ |EB| = 8cm

|BD| = |DC| 
|CF |
|CD|
|DF |
⇒
=
=
|CE|
|CB|
|BE|
|EF | = |F C| 
⇒
|DF |
1
= ⇒ |DF | = 4cm
8
2
8. DİK ÜÇGENLERDE METRİK BAĞINTILAR
Tanım 3.4. Bir dik üçgende dik açının gördüğü kenara hipotenüs denir.
Teorem 3.18. Bir dik üçgende hipotenüse ait yüksekliği tanımlayan doğru
parçası, bu üçgeni bir birine ve kendine benzeyen iki üçgene ayırır.
△
Bir ABC dik üçgeninde,
(8.8)
İspat:

△
△
△
[AB] ⊥ [BC] 
⇒ ABC ∼ ADB ∼ BDC.
[BD] ⊥ [AC] 
8. DİK ÜÇGENLERDE METRİK BAĞINTILAR
45
A
D
2
1
B
C
Şekil 28

o
m(B̂1 ) + m(Ĉ) = 90 
⇒ B̂1 ∼
= Â,
o

m(Â) + m(Ĉ) = 90

m(B̂2 ) + m(Â) = 90o 
⇒ B̂2 ∼
= Ĉ,
o

m(Ĉ) + m(Â) = 90


 ∼
B̂
= 1 


△
△
∼
⇒ ABC ∼ BDC
B̂ = D̂



Ĉ ∼
= Ĉ 

∼

 =  


△
△
⇒ ABC ∼ ADB
B̂ ∼
D̂
=



∼ B̂2 
Ĉ =
∼ bağıntısının geçişme özelliğinden 8.8 elde edilir.
a
x
=
orantısını sağlayan x ∈ R+
x
b √
sayısına a ile b nin geometrik ortası denir ve x = a.b ile gösterilir.
Tanım 3.5. a, b ∈ R+ olmak üzere
Bu tanım ve yukarıdaki teoremden aşağıdaki sonuçları verebiliriz.
Sonuç 3.10. Bir dik üçgende hipotenüse ait yükseklik, hipotenüs üzerinde
ayırdığı doğru parçalarının uzunluklarının geometrik ortasıdır.
Bu sonucun yukarıdaki şekle göre matematiksel ifadesi
△
△
ADB ∼ BDC ⇒
|AD|
|BD|
=
⇒ |BD|2 = |AD||DC| = h2
|BD|
|DC|
bu eşitliğe dik üçgende yükseklik bağıntısı denir.
Sonuç 3.11. Bir dik üçgende herbir dik kenar, hüpotenüs ile hipotenüsün
kendi tarafında kalan paçanın geometrik ortasıdır.
46
3. ÜÇGENLER
(8.9)
|AB|2 = |AC||AD|
(8.10)
|BC|2 = |AC||CD|
bu eşitliklere dik üçgende kenar bağıntısı denir.
Bu sonuçtan aşağıdaki teorem elde edilir.
Teorem 3.19. (Pisagor Teoremi) Bir dik üçgende dik kenarların uzunluklarının karelerinin toplamı hüpotenüs uzunluğunun karesine eşittir.
yani
|AB|2 + |BC|2 = |AC|2 dir.
△
İspat: Şekil 27 de verilen ABC üçgeninin [AC]-kenarını bir kareye, bu
kareyede aşağıdaki şekilde bir büyük kareye tamamlayalım. Bu durumda,
A
b
B
a
C
c
Şekil 29
büyük karenin kenar uzunluğu (a + c) − br olup alanı
a.c
+ b2
=⇒ a2 + c2 = b2 elde edilir.
A = (a + c)2 = a2 + 2ac + c2 = 4
2
8. DİK ÜÇGENLERDE METRİK BAĞINTILAR
47
△
Teorem 3.20. Bir ABC ninde D ∈ [BC] olmak üzere,


|BD| = m 


|DC| = n
dir.



|AD| = x 
⇒ x2 =
mb2 + nc2
− mn
m+n
İspat:
A
B
H
D
C
Şekil 30
A noktasının [BC] üzerindeki dikme ayağına H, |HD| = k diyelim. Bu
durumda, elde edilen dik üçgenlere Pisagor Teoremi uygulanırsa,
△
ABH- dik üçgeninden
△
AHD- dik üçgeninden
△
AHC- dik üçgeninden
c2 = h2 + (m − k)2
x2 = h2 + k 2
b2 = h2 + (n + k)2
yazılabilir. Buradan da
mb2 = mh2 + mn2 + mk 2 − 2mnk
nc2 = nh2 + nm2 + nk 2 + 2mnk
elde edilir. Bu iki eşitlik taraf tarafa toplanırsa,
mb2 + nc2 = (m + n)(h2 + mn + k 2 )
⇒ h2 + k 2 = x2 =
elde edilir.
mb2 + nc2
− mn
m+n
48
3. ÜÇGENLER
Bu teoremin bir sonucu olarak verilen, aşağıdaki sonuçlardan biri diğerini
gerektirir.
Sonuç 3.12. Eğer [AD], Â sına ait açıortay ise,
mb = nc
olup
x2 = bc − mn dir.
Sonuç 3.13. Eğer [AD], [BC] kenarına ait kenarortay ise, m = n olup
a2
1
x2 = (b2 + c2 − ) dir.
2
2
Sonuç 3.14. Eğer m(Â = 90o ) ise, b2 + c2 = a2 olup
x=
a
dir.
2
BÖLÜM 4
DÖRTGENLER
Tanım 4.1. Düzlemde en az üçü doğrusal olmayan dört nokta ve bu noktaların ikişer ikişer birleştirilmesiyle oluşan doğru parçalarınn birleşim kümesine dörtgen denir.
D
c
d
C
b
a
A
B
Şekil 1. Dörtgen
Dörtgenler sol alt köşeden başlayarak köşe noktalarının saatin ters yönünde
sıralanmasıyla gösterilir, ABCD - dörtgeni gibi. Kenarlar üçgenlerden farklı
olarak, her kenar takip ettiği köşenin küçük harfiyle gösterilir.
Bu tanıma göre bir dörtgenin temel özelikleri,
* Düzlemsel bir şekil olması,
* Dört köşesi ve dört kenarının olması,
* Basit kapalı bir şekil olması
Tanım 4.2. Bir dörtgende komşu olmayan iki köşeyi birleştiren doğru
parçasına köşegen denir.
Her dörtgen iki köşegene sahiptir. ABCD - dörtgeninin köşegenleri [AC]
ve [BD] dir. Bir dörtgen bir kenarları ortak olan iki üçgenden oluşur. Buna
göre bir dörtgenin iç açılarının ölçüleri toplamı 2 × 180o = 360o dir.
49
50
4. DÖRTGENLER
Teorem 4.1. Bir dörtgende komşu iki köşedeki iki açının açıortayının
oluşturduğu açının ölçüsü, diğer iki köşedeki iç açıların ölçüleri toplamının
yarısına eşittir.
D
K
C
A
B
Şekil 2. Açıortay
1
ˆ
m(AKB)
= [m(Ĉ) + m(D̂)]
2
△
İspat: KAB- üçgenin de
ABCD - dörtgeninde
m(K̂) +
m(Â) m(B̂)
+
= 180o
2
2
m(Â) + m(B̂) + m(Ĉ) + m(D̂) = 360o
Bu eşitlğin her iki tarafı ikiye bölünürse,
m(Â) m(B̂) m(Ĉ) m(D̂)
m(Â) m(B̂)
+
+
+
= 180o = m(K̂) +
+
2
2
2
2
2
2
1
ˆ
⇒ m(AKB)
= [m(Ĉ) + m(D̂)]
2
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
Dörtgenler, kenar ve açı özeliklerine göre sınıflandırılırlar. Bu sınıflandırmada yer alan dörtgenler yamuk, paralel kenar, eşkenar dörtgen, dikdörtgen,
kare ve deltoid’dir.
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
51
1.1. Yamuk. .
İki kenarı paralel olan dörtgenlere yamuk, paralel olan kenarlara taban adı
verilir.
E
D
C
A
B
Şekil 3. Yamuk
Teorem 4.2. Bir yamukta paralel olmayan kenarlardan her birinin uçlarındaki açılar bütünler açılardır.
Şekil (3) de verilen ABCD - yamuğunda
m(Â) + m(D̂) = 180o
ve
m(B̂) + m(Ĉ) = 180o
~ yönünde uzatıp üzerinde bir E noktası seçeİspat: [AD] - kenarını AD
lim. Bu durumda,
ˆ (yöndeş açılar) ⇒ m(Â) = m(CDE)
ˆ
 ∼
= CDE
ˆ ( kendisi)
D̂ ∼
= ADC
ˆ
⇒ m(D̂) = m(ADC)
ˆ
ˆ
⇒ m(Â)+m(D̂) = m(ACD)+m(
CDE)
= 180o
elde edilir, benzer düşünceyle m(B̂) + m(Ĉ) = 180o olduğun da gösterilebilir.
Tanım 4.3. Bir yamukta paralel olmayan iki kenarın orta noktalarını
birleştiren doğru parçasına orta taban denir.

|AM | = |M D| 
⇒ [M N ] orta tabandır.
|BN | = |N C| 
52
4. DÖRTGENLER
D
C
M
N
K
L
A
B
Şekil 4. Orta taban
Bu tanımdan aşağıdaki sonuçlar elde edilir.
Sonuç 4.1. Bir yamukta orta tabanın uzunluğu diğer tabanların uzunlukları toplamının yarısına eşittir.
1
|M N | = (|AB| + |CD|)
2
Sonuç 4.2. Bir yamukta orta tabanın köşegenler arasında kalan parçasının
uzunluğu taban uzunlukları farkının yarısına eşittir.
İspat:
1
|KL| = (|AB| − |CD|)
2
△
△
A.A.A benzerlik aksiyomuna göre AM K ∼ ADC
⇒
|M K|
1
|M K|
1
|AM |
=
⇔ =
⇒ |M K| = |DC|
|AD|
|DC|
2
|DC|
2
△
△
A.A.A benzerlik aksiyomuna göre DM L ∼ DAB
⇒
|M L|
|DM |
1
|M L|
1
=
⇔ =
⇒ |M L| = |AB|
|AB|
|DA|
2
|AB|
2
1
1
1
|KL| = |M L| − |M K| = |AB| − |DC| = (|AB| − |DC|) elde edilir.
2
2
2
Örnek 1.1. Bir ABCD- yamuğunun kenar uzunlukları sırasıyla
|AB| = 14, |BC| = 8, |CD| = 4
ve
|DA| = 6 cm,
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
53
E, (Â, D̂) açıortaylarının kesişim noktası ve
F, (B̂, Ĉ) açıortaylarının kesişim noktası ise, |EF | =?
Çözüm: Öncelikle problemde verilenlere göre geometrik şeklimizi çizelim.
K
D
H
β
C
β
E
F
α
α
A
B
L
Şekil 5
ˆ
m(Â) + m(D̂) = 180o olduğundan α + β = 90o olup m(AED)
= 90o dir.
E noktası açıortaylarının kesişim noktası olduğundan |EK| = |EH| = |EL|
olup E noktası orta taban üzerindedir. Orta taban [M N ] dersek [EM ] ,
△
1
AED diküçgeninde hipotenüse ait kenarortay olup |EM | = |AD| = 3 cm
2
1
dir. Benzer düşünceyle |F N | = |BC| = 4 cm dir.
2
14 + 4
a+c
=
= 9 ⇒ |EF | = 9 − (3 + 4) = 2 cm bulunur.
⇒ |M N | =
2
2
1.2. İkizkenar Yamuk. :
Paralel olmayan kenarları eş olan yamuğa ikizkenar yamuk denir.
[AD] ∼
= [BC] ⇒ ABCD - yamuğu bir ikiz kenar yamuktur.
Bir ikizkenar yamuk, yamuğa ilaveten aşağıdaki özeliklere de sahiptir.
1) bir tabanın iki ucundaki açılar eştir, yani  ∼
= B̂ ve Ĉ ∼
= D̂.
2) köşegenler eştir, yani |AC| = |BD|
54
4. DÖRTGENLER
D
C
A
E
B
Şekil 6. İkizkenar yamuk
İspat 1: C köşesinden [AD] - kenarına bir paralel çizip, [AB] - kenarıyla
kesim noktasına E diyelim. Bu durumda
 ∼
= Ê - yöndeş açılar,
△
|CE| = |DA| = |CB| olduğundan CEB ni ikiz kenar üçgen olup
Ê ∼
= B̂ - taban açılar.
Ohalde  ∼
= Ê ∼
= B̂ ⇒ Â ∼
= B̂ dir.
Ĉ ∼
= D̂ olduğuda benzer şekilde gösterilebilir.
1.3. Paralelkenar. :
Karşılıklı kenarları paralel olan dörtgene paralel kenar denir.
D
C
∼
K
∼
A
B
Şekil 7. Paralelkenar

[AB] // [DC] 
⇒ ABCD - dörtgeni bir paralelkenardır.
[AD] // [BC] 
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
55
Bir paralel kenar, yamuğa ilaveten aşağıdaki özeliklere de sahiptir.
Bir ABCD - paralel kenarında
1) karşılıklı açılar birbirine eştir, Â ∼
= Ĉ, B̂ ∼
= D̂
2) karşılıklı kenarlar birbirine eştir, [AB] ∼
= [DC], [AD] ∼
= [BC].
3) köşegenler birbirini ortalar, yani köşegenlerin kesişim noktası K ise,
1
1
ve
|BK| = |KD| = |BD|
|AK| = |KC| = |AC|
2
2
4) bir kenarın iki ucundaki açılar bütünlerdir.
1.4. Eşkenar Dörtgen. :
Dört kenarı eş olan paralel kenara eşkenar dörtgen denir.
D
A
C
B
Şekil 8. Eşkenar dörtgen
[AB] ∼
= [BC] ∼
= [CD] ∼
= [DA] ⇒ ABCD - dörtgeni bir eşkenar dört-
gendir.
Bir eşkenar dörtgen, yamuk ve paralel kenara ilaveten iki ikizkenar üçgenin birleşimi olduğunda şu özeliklere de sahiptir.
1) her köşegen birleştirdiği köşelerdeki açıların açıortayıdır,
2) her bir köşegen diğer köşegenin orta dikmesidir.
1.5. Dıkdörtgen. :
Açıları dik açı olan paralel kenara dikdörtgen denir.
Dikdörtgen paralel kenardan farklı olarak, açıları dik açı ve köşegenleri
eştir.
56
4. DÖRTGENLER
D
C
A
B
Şekil 9. Dikdörtgen
1.6. Kare. :
Kenarları eş olan dik dörtgene kare denir.
D
C
K
A
B
Şekil 10. kare
Bir karede eşkenar dörtgen ve dikdörtgenden farklı olarak,
1) köşegen uzunlukları eşit (eşkenar dörtgenden farkı)
2) köşegenler birbirinin orta dikmesidir (dikdörtgenden farkı)
3) Ayrıca her kare köşegenler yardımıyla dört tane, eş ikizkenar dik üçgene ayrılır, yani K - köşegenlerin kesişim noktası olmak üzere,
△
△
△
KAB, KBC, KCD
ve
△
KDA
dik üçgenleri eş üçgenlerdir.
Örnek 1.2. Bir ABCD- karesinin köşegenlerinin kesişim noktası E,
Â- sının açıortayının [BE] ve [BC] ile kesişim noktaları sırasıyla F ve G
√
olmak üzüre; |EF | = 2 cm ise |GC| = x kaç cm dir?
Çözüm:
G noktasının [AC] üzerindeki dikme ayağına H dersek,
△
[AG, ABC ninde Â- sının açıortayı olduğundan |GB| = |GH| = a olsun.
1. DÖRTGEN ÇEŞİTLERİ VE ÖZELİKLERİ
D
57
C
H
x
E
F
A
G
B
Şekil 11
△
△
Bu durumda HGC nin açıları (90o , ?, 45o ) ⇒ m(Ĝ) = 45o olup HGC ni bir
ikizkenar üçgendir, yani
|HG| = |HC| = a ⇒ x =
√
2a ⇒ |BC| = a +
√
2a ⇒ |AC| = 2a +
√
2a
√
√
√
|AC|
2
2
⇒ |EC| =
=a+
a ⇒ |EH| =
a ⇒ |AH| = a + 2a
2
2
2
A.A. benzerlik sonucuna göre
√
2
√
a
a+
△
△
2
|EF |
|AE|
2
√
=
=
⇔
⇒a=2
AEF ∼ AHG ⇒
|AH|
|HG|
a
a + 2a
√
⇒x=2 2
1.7. Deltoid. :
Tanım 4.4. Bir köşegene göre simetrik olan dörtgene deltoid, bu köşegenin doğrultusuna simetri ekseni denir.
Deltoid, bir üçgenin en uzun kenarına göre simetrisi alınarak elde edilebileceğinden, tabanları ortak olan iki ikizkenar üçgenden oluşmuştur. Buna göre
eşkenar dörtgen ve kare birer deltoidtir.
ABCD- dörtgeni, simetri ekseni BD−doğrusu olan bir deltoidtir.
Deltoidin Özelikleri:
1) Simetri ekseninde birleşen kenarlar eştir,
[AB] ∼
= [BC]
ve [AD] ∼
= [DC] dir,
2) Simetri eksenini gören açıları eştir, yani  ∼
= Ĉ dir.
3) [BD] simetri köşegeni, B̂ ve D̂ açılarının açıortayıdır,
4) Köşegenleri dik kesişir, m(K̂) = 90o
58
4. DÖRTGENLER
A
.
B
D
K
C
Şekil 12. Deltoid
5) Uzun olan köşegen kısa olanı ortalar,
1
[AC] ⊥ [BD] ve |AK| = |KC| = |AC| dir.
2
2. ÇOKGENLER
Genel olarak n ≥ 5 olduğunda n−gen yerine çokgen kavramı kullanılır.
Çokgenler kenar doğrularının, kenarları kesip kesmemesine göre iki sınıfa
ayrılır.
2.1. Dişbükey ve İçbükey Çokgenler. .
Bir çokgenin kenar doğrularının hiçbiri çokgeni kesmiyorsa bu çokgenlere
dışbükey çokgen, bazı kenar doğruları çokgeni kesiyorsa bu tür çokgenlere
de içbükey çokgen denir.
B
A
B
Şekil 13. Dışbükey Çokgen
A
İçbükey Çokgen
Bir çokgen ile iç noktalarının kümesine çokgensel bölge denir, bu bölgeyi
B ile gösterelim. ∀A, B ∈ B için [AB] ⊂ B oluyorsa B bölgesine konveks
bölge aksi halde konveks olmayan bölge denir. Bir konveks bölge oluşturan
çokgenler dışbükeydir.
2. ÇOKGENLER
59
Aksi belirtilmedikçe çokgen denildiğinde bir dışbükey çokgen kastedilir.
ÇOKGENLERİN ÖZELİKLERİ:
n ≥ 3 olmak üzere n-kenarlı bir çokgende;
1) Bir köşeden çizilen köşegenlerle (n-2)-tane üçgen oluşur, buna göre bir
çokgende iç açıların ölçüleri toplamı (n − 2) × 180o dir.
n
X
i=1
m(Âi ) = (n − 2) × 1802
2) Herhangi bir köşede oluşan iç açı ile dış açı komşu bütünler açılardır.
∀i
için
m(Âi ) + m(Â′i ) = 180o
3) Bir çokgenin tüm köşelerinin birleştirilmesiyle oluşan doğru parçalerından n−tanesi kenar, diğerleri köşegendir. Buna göre n− kenarlı bir çokgenin
köşegen sayısı,
s(K) = P (n, 2) − n =
n(n − 3)
n(n − 1)
−n=
2
2
n = 3 için s(K) =
3(3 − 3)
= 0,
2
üçgenin köşegeni yoktur,
n = 4 için s(K) =
4(4 − 3)
= 2,
2
dörtgenin 2 köşegeni vardır,
...
n = 9 için s(K) =
9(9 − 3)
= 27 vs.
2
2.2. Düzgün Çokgenler.
Tanım 4.5. Kenarları ve iç açıları eş olan çokgenlere düzgün çokgen
denir. Mesela eşkenar üçgen, kare birer düzgün çokgendir.
* DÜZGÜN ÇOKGENLERİN ÖZELİKLERİ
n−kenarlı bir düzgün çokgende,
1) her bir iç açısının ölçüsü, yani her i = 1,2, ... ,n için
60
4. DÖRTGENLER
(n − 2)180
360
= 180o −
n
n
ve herbir dış açısının ölçüsü,
m(Âi ) =
m(Â′i ) =
360
n
Örnek 2.1. Bir düzgün altıgenin her bir iç açısının ölçüsü,
A5
A4
A6
A3
60o
120o
A1
A2
Şekil 14. Düzgün Altıgen
m(Âi ) =
(6 − 2)180
360
= 180o −
= 120o
6
6
ve dış açısının ölçüsü,
m(Â′i ) =
360
= 60o
6
2) Eşit sayıda kenarı birleştiren köşegenler eştir.
[A1 A3 ] ∼
= [A2 A4 ] ∼
= [A3 A5 ]
[A1 A4 ] ∼
= [A2 A6 ] vs...
= [A1 A6 ] ve [A1 A5 ] ∼
= [A2 A5 ], [A2 A5 ] ∼
3) Kenar sayısı çift olan düzgün çokgenlerde karşılıklı kenarlar paraleldir.
[A1 A2 ]//[A4 A5 ] , [A2 A3 ]//[A5 A6 ] ve [A3 A4 ]//[A6 A1 ]
2. ÇOKGENLER
A5
61
A4
A3
A6
A8
A1
A1
A2
Şekil 15. n - çift
[A1 A2 ]//[A5 A6 ] ve [A2 A3 ]//[A6 A7 ] vs...
4) Kenar sayısı tek olan düzgün çokgenlerde karşı kenara çizilen dik karşı
kenarı ortalar veya köşeden kenarın ortasına çizilen doğru parçası kenara
A
diktir.
B
E
C
D
H
Şekil 16. n - tek
[AH] ⊥ [CD] ⇔ |CH| = |HD|
Örnek 2.2. Köşegen sayısı kenar sayısının altı katı olan bir düzgün çokgenin,
a) kenar sayısı nedir?
b) her bir iç ve dış açısının ölçüsü nedir?
5) Bir düzgün çokgende kenar sayısı arttıkça düzgün çokgen çembere,
çokgensel bölgede daireye yaklaşır.
62
4. DÖRTGENLER
Önce bir düzgün çokgen olan eşkenar üçgen alarak ağırlık merkezini bulalım.
b
b
b
b
b
b
b
b
b
b
b
b
Şekil 17
Bu noktanın köşelere olan uzaklığı sabit tutularak kenar sayısını ikiye
katlarsak düzgün altıgen elde edilir. Düzgün altıgen üçgene göre daha yuvarlak bir şekildir. Düzgün altıgenin de kenar sayısını ikiye katlar ve sonra
yine sürekli ikiye katlarsak o kadar çok kenar olacaktır ki, bu çokgen bir çember gibi görünecektir. Böylece düzgün çokgen çembere, çokgensel bölgede
daireye dönüşür. Bu sayede kenarlar kullanılarak yapılan bazı cebirsel işlemleri kenarı olmayan daire ve benzeri kavramlar için de kullanılma imkanı
doğmuştur.
BÖLÜM 5
ÇEMBERLER
Tanım 5.1. Düzlemde sabit bir noktadan eşit uzaklıkta bulunan noktaların kümesine çember, bu sabit noktaya merkez ve eşit uzaklığa da yarıçap
denir.
Buna göre bir çember, merkez noktası ve yarıçap uzunluğu ile belli olup,
M -merkezli ve r-yarıçaplı bir çember C(M, r)−ile gösterilir, yani
C(M, r) = {P ∈ D : |M P | = r br} kümesidir.
k
n
t
T
r
M
D
K
L
Şekil 1. Çember
1. ÇEMBERLE İLGİLİ KAVRAMLAR
1) Teğet: Çemberle bir ortak noktası olan doğruya teğet denir.
C ∩ t = {T } ⇒ t−doğrusuna teğet T -noktasına değme noktası denir.
2) Kesen: Çemberle iki ortak noktası olan doğruya kesen denir.
C ∩ k = {T, K} ⇒ k−doğrusuna kesen denir.
63
64
5. ÇEMBERLER
3) Kiriş: Çemberin farklı iki noktasını birleştiren doğru parçasına kiriş
denir. [T K]−doğru parçası bir kiriştir.
4) Çap: Merkezden geçen kirişe çap denir. M ∈ [T L]- olduğundan
[T K]−doğru parçası bir kiriştir.
5) Normal: Çemberin herhangi bir teğetine, değme noktasında dik olan
doğruya çemberin o noktadaki normali denir. n-doğrusu T -noktasındaki
normaldir.
Sonuç 5.1. Bir çemberin herhangi bir noktadaki normali çemberin merkezinden geçer, yani M ∈ n dir.
2. ÇEMBERİN DÜZLEMDE AYIRDIĞI BÖLGELER
Düzlemde basit kapalı bir eğri olan çember, bulunduğu düzlemde biri
kendisi olmak üzere, üç ayrık küme oluşturur.Bu kümeler;
Dış Bölge
M
Y
X
İç Bölge
D
Şekil 2. Bölgeler
1) Çember C(M, r) = {P ∈ D : |M P | = r br} kümesidir.
2) Çemberin iç bölgesi Ci (M, r) = {X ∈ D : |M X| < r br}
3) Çemberin dış bölgesi Cd (M, r) = {Y ∈ D : |M Y | > r br}
Yarıçap uzunlukları eşit olan çemberlere eştir .
3. BİR DOĞRU İLE BİR ÇEMBERİN BİRBİRİNE GÖRE KONUMLARI
65
3. BİR DOĞRU İLE BİR ÇEMBERİN BİRBİRİNE GÖRE
KONUMLARI
Aynı düzlemde yatan bir d doğrusu ve bir C(M, r) çemberi verildiğinde,
merkez noktanın doğruya olan uzaklığı |M H| = h olmak üzere; aşağıdaki üç
ihtimal söz konusudur.
M
d=k
d=t
T
d
H
Şekil 3. Çember ve doğru
1) h < r ⇒ C ∩ d = {A, B} doğru çemberin bir kesenidir,
2) h = r ⇒ C ∩ d = {T } doğru çembere teğettir,
3) h > r ⇒ C ∩ d = {} doğru çemberi kesmez.
Teorem 5.1. Bir çemberin merkezinden herhangi bir kirişe inilen dikme,
bu kirişi ortalar, yani bir C(M, r) çemberinde [AB] bir kiriş ve
[M H] ⊥ [AB] ⇒ |AH| = |HB|
dir.
M
A
H
Şekil 4
B
66
5. ÇEMBERLER
△
İspat: |AM | = |BM | = r olduğundan, M AB bir ikizkenar üçgendir. O
halde [M H] yüksekliği aynı zamanda kenarortay olacağından,
[M H] ⊥ [AB] ⇒ |AH| = |HB|.
Bu teoremden aşağıdaki sonuçlar verilebilir;
1) Bir çemberde herhangi bir kirişin orta dikmesi, çemberin merkezinden
geçer.
2) Bir çemberde herhangi bir kirişin orta noktasını çemberin merkezine
birleştiren doğru, kirişe diktir.
3) Bir çemberde eş kirişlerin merkeze olan uzaklıkları eşittir, yani
|AB| = |BC| ⇒ |M H1 | = |M H2 |
4) Bir çemberde merkezden eşit uzaklıktaki kirişlerin uzunlukları eşittir.
5) Bir çemberde uzun olan kiriş merkeze daha yakındır.
6) Bir çemberin iç bölgesinde verilen bir A için, bu noktadan geçen en
kısa kiriş, [M A] na dik olan kiriştir.
4. İKİ ÇEMBERİN BİRBİRİNE GÖRE KONUMLARI
Aynı düzlemde yatan iki çemberin birbirine göre konumları, merkez noktaları arasındaki uzaklığa ve yarıçap uzunluklarına bağlıdır.
Buna göre
C(M1 , r1 ) ve C̃(M2 , r2 ) herhangi iki çember ve |M1 M2 | = d olmak üzere
aşağıdaki ihtimaller söz konusudur.
4.1. Kesişmeme Durumu. . a) r1 + r2 < d ⇒ C ∩ C̃ = ∅
r1
M1
r2
d
Şekil 5
M2
4. İKİ ÇEMBERİN BİRBİRİNE GÖRE KONUMLARI
b) d < r1 − r2 ⇒ C ∩ C̃ = ∅
M1
67
c) d = 0 ∧ r1 6= r2 ⇒ C ∩ C̃ = ∅
M2
M1 = M2
Şekil 6
4.2. Teğet Olma Durumu. .
a) r1 + r2 = d ⇒ C ∩ C̃ = {T } (dışdan teğet)
M1
M2
M1
M2
Şekil 7
b) r1 − r2 = d ⇒ C ∩ C̃ = {T } (içten teğet)
4.3. Kesişme Durumu. r1 + r2 > d ⇒ C ∩ C̃ = {A, B}
A
M1
M2
B
Şekil 8
Sonuç 5.2. Eğer iki çember kesişiyorsa, en fazla iki noktada kesişir. Bu
iki noktanın belirttiği doğru parçası bu iki çemberin ortak kirişidir.
68
5. ÇEMBERLER
5. ÇEMBERDE YAYLAR VE AÇILAR
Tanım 5.2. Çemberin bir parçasına yay denir.
Bir C(M, r) çemberi üzerinde alınan A ve B gibi iki nokta, çemberi iki
yay parçasına ayırır. Bu yaylar ya eşit uzunlukta, ya da biri diğerinden
küçüktür. AB-yayı denildiğinde bu iki yaydan küçük olan anlaşılır ve bu
d ile gösterilir. Büyük olan yay ise, üzerinde A ve B den fraklı bir
yay AB
\ şeklinde gösterilir. Yayın ölçü birimi derecedir.
X noktası alınarak AXB
B
\
AXB
M
d
AB
A
r
X
Şekil 9
d yayının ölçüsü m(AB)
d ile,
Çember yayının ölçüsü 360o kabul edilmiştir. AB
d ile gösterilir.
bu yayın uzunluğu ise |AB|
Çember Yardımıyla Tanımlanan Açı Çeşitleri
5.1. Merkez Açı. Köşesi bir çemberin merkez noktası olan açıya merkez
açı denir.
B
M
A
Şekil 10
Bir merkez açıda, açının kolları arasında kalan yay parçasına o açının
ˆ B−merkez açısının gördüğü yay AB−
d yayıdır.
gördüğü yay denir. AM
5. ÇEMBERDE YAYLAR VE AÇILAR
69
*Çemberin bir yayının ölçüsü, bu yayı gören merkez açının ölçüsüne eşittir.
* Ölçüleri eşit olan yayalar eştir.
Merkez açıyla ilgili aşağıdaki sonuçları verebiliriz.
Sonuç 5.3. Bir çemberde veya eş çemberlerde
1) Eş yayların, gördükleri merkez açılar eştir,
2) Eş merkez açıların, gördükleri yayla eştir,
3) Eş yayların, gördükleri kirişler eştir,
4) Eş kirişlerin, gördükleri yayla eştir,
5) Bir kirişe dik olan çap, bu kirişe ait olan yayı ortalar.
M
A
B
C
Şekil 11. Merkez açı
(5.1)
d = |CB|
d = 1 |AB|
d
[M C] ⊥ [AB] ⇒ |AC
2
△
İspat 5: |AM | = |BM | = r olduğundan M AB bir ikizkenar üçgendir.
Bir ikizkenar üçgende tabana ait yükseklik hem açıortay hem de kenarortay
olduğundan
ˆC∼
ˆ B ⇒ |AC
d = |CB|.
d
AM
= CM
5.2. Çevre Açı. Köşesi bir çemberin üzerinde olup, kenarları bu çemberi kesen açıya çevre açı denir.
Teorem 5.2. Bir çevre açının ölçüsü, aynı yayı gören merkez açının
ölçüsünün yarısına eşittir,
70
5. ÇEMBERLER
B
A
M
D
C
Şekil 12. Çevre açı
(5.2)
1
ˆ
ˆ C)
m(BAC)
= m(BM
2
△
△
İspat: Şekil 12 de M AB ve M AC üçgenleri birer ikizkenar üçgen olup
ˆ D) = 2α - dış açı
m(M ˆAB) = m(M ˆBA) = α ⇒ m(BM
ˆ D) = 2β
m(M ˆAC) = m(M ˆCA) = β ⇒ m(CM
1
ˆ C) = 2(α + β) ⇒ m(BAC)
ˆ
ˆ C)
⇒ m(BM
= α + β = m(BM
2
Bu teoremden aşağıdaki sonuçları verebiliriz.
Sonuç 5.4. Bir çemberde veya eş çemberlerde,
1) Bir çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir,
(5.3)
1 d
ˆ
m(BAC)
= m(BC)
2
2) Çapı gören çevre açısının ölçüsü 90o dir,
3) Aynı yayı gören iki çevre açı eştir,
4) Parelel iki kiriş arasında kalan yay parçalarının uzunlukları eşittir,
(5.4)
d = |BD|
d
|AC|
5) Herhangi bir kiriş ile buna paralel bir teğet arasındaki yay parçalarının
uzunlukları eşittir.
(5.5)
d | = |T
d
|AT
B|
5. ÇEMBERDE YAYLAR VE AÇILAR
71
T
A
B
M
C
D
Şekil 13
5.3. Teğet-Kiriş Açı. Köşesi bir çemberin üzerinde olup, kenarlar biri
çembere teğet diğeri kiriş olan açıya teğet-kiriş açı denir.
B
C
M
A
Şekil 14. Teğet-kiriş açı
ˆ
ABC−
açısı bir teğet-kiriş açıdır.
Teorem 5.3. Bir teğet-kiriş açının ölçüsü gördüğü yayın ölçüsünün yarısına
eşittir, yani
1 d
ˆ
m(ABC)
= m(AB)
2
(5.6)
△
İspat: A ve B noktalarını M noktasıyla birleştirelim. Bu durumda, M AB
üçgeni bir ikizkenar üçgen olup taban açılarının
ölçüsüne α dersek,


m(M̂ ) = 180 − 2α = 2(90 − α)
ˆ
⇒ m(M̂ ) = 2m(ABC)

ˆ
[M B] ⊥ [BC] ⇒ m(ABC) = 90 − α
1
1 d
ˆ
⇒ m(ABC)
= m(M̂ ) = m(AB)
olur.
2
2
5.4. İç Açı. Bir çemberde kesişen herhangi iki kirişin oluşturduğu açıya
iç açı denir.
72
5. ÇEMBERLER
B
K
C
D
M
A
Şekil 15. İç açı
Teorem 5.4. Bir iç açının ölçüsü, kenarları arasında kalan yayların
ölçüleri toplamının yarısına eşittir, yani
1
d + m(BD)]
d
ˆ
m(AKC)
= [m(AC)
2
(5.7)
İspat: A ile B noktalarını birleştirelim. Bu durumda,
1 d
1 d
ˆ
+ m(AC)
m(BKD)
= m(Â) + m(D̂) = m(BD)
2
2
1
d + m(BD))
d
= (m(AC)
2
elde edilir.
5.5. Dış Açı. Köşesi çemberin dışında, kenarları çemberi kesen veya
teğet olan açıya dış açı denir.
C
B
A
M
D
E
Şekil 16. Dış açı
Teorem 5.5. Bir dış açının ölçüsü, kenarların çemberden ayırdığı ve
açının iç bölgesinde bulunan büyük yay ile küçük yayın ölçüleri farkının
yarısına eşittir, yani
6. ÇEMBERDE YAY VE TEĞET PARÇALARI UZUNLUĞU HESABI
(5.8)
73
1
d − m(BD)]
d
m(Â) = [m(CE)
2
İspat: B ile E noktalarını birleştirelim. Bu durumda,
ˆ
m(CBE)
= m(Â) + m(Ê)
1 d
1 d
ˆ
m(Â) = m(CBE)
− m(Ê) = m(CE)
− m(BD)
2
2
1
d − m(BD))
d
= (m(CE)
2
elde edilir.
6. ÇEMBERDE YAY ve TEĞET PARÇALARI UZUNLUĞU
HESABI
6.1. Çemberde yay parçası uzunluğu. Bir C(M, r) çemberi verildiğinde, çevre uzunluğunun çap uzunluğuna oranı yaklaşık olarak 3.14 gibi
sabit bir değer olup matematikte pi sayısı olarak bilinir. Buna göre, C(M, r)
B
α
A
M
Şekil 17
C
=π∼
= 3.14... yazılır. R = 2r olup ⇒ C = 2πr elde edilir,
R
yani r-yarıçaplı çember yayının uzunluğu 2πr birim dir. Herhangi bir yay
çemberi için
parçasının uzunluğu da, gördüğü merkez açının ölçüsü α olmak üzere
(6.9)
birim olarak bulunur.
d = 2πr
|AB|
α
α
= πr
360
180
74
5. ÇEMBERLER
6.2. Çemberde teğet parçası uzunluğu. Bir C(M, r) çemberi ile dış
bölgesinde bir A noktası verildiğinde, A noktasından çembere iki teğet ışın
vardır, bunlar
B
A
M
C
Şekil 18
[AB ve [AC ışınlarıdır. [AB] ve [AC] doğru parçalarına teğet parçaları
denir.
Teorem 5.6. Bir çembere dışındaki bir noktadan çizilen teğet parçaları
eştir, yani
|AB| = |AC| dir.
İspat: A, B ve C noktalarını çemberin merkez noktasıyla birleştirelim.
Bu durumda; hipotenüsleri ve birer dik kenarları eş olan iki dik üçgen
△
△
BAM ∼
= CAM
elde edilir ve bu üçgenler eştir. Eş üçgenlerin karşılıklı kenarları eş olduğundan |AB| = |AC| dir.
Bu teoremden aşağıdaki sonucu elde ederiz.
Sonuç 5.5. Bir çembere dışındaki bir noktadan iki teğet çizildiğinde bu
noktayı merkeze birleştiren doğru bu noktada oluşan açının açıortayıdır.
ˆ ) = m(CAM
ˆ ) = 1 m(BAC)
ˆ
m(BAM
2
6. ÇEMBERDE YAY VE TEĞET PARÇALARI UZUNLUĞU HESABI
75
6.3. İki çemberin ortak teğetleri. Aynı düzlemde yatan iki çember
verildiğinde her birine teğet olan doğruya bu iki çemberin ortak teğeti denir.
Ortak teğetler dış ortak teğet ve iç ortak teğet olmak üzere ikiye ayrılır.
6.3.1. Dış ortak teğet: Çemberlerin merkez noktalarının oluşturduğu doğru
parçasını kesmeyen ortak teğetlere dış ortak teğet denir.
M1
M2
Şekil 19. Dış ortak teğetler
6.3.2. İç ortak teğet: Çemberlerin merkez noktalarının oluşturduğu doğru
parçasını kesen ortak teğetlere iç ortak teğet denir.
M1
M2
Şekil 20. İç ortak teğetler
Tanım 5.3. İki çemberin bir ortak teğetinin bu çemberler üzerindeki değme
noktalarıyla sınırlanan doğru parçasına ortak teğet parçası denir.
Teorem 5.7. İki çemberin,
a) Dış ortak teğet parçaları eştir,
76
5. ÇEMBERLER
B
A
D
M1
M2
C
Şekil 21. Ortak teğet parçaları
b) İç ortak teğet parçaları eştir.
İspat a) Ortak teğet doğrularının kesişim noktasına K diyelim. Bu
durumda Teorem 6 dan
B
A
K
C
D
Şekil 22. Dış ortak teğet parçaları
|KB| = |KD| ve |KA| = |KC|
bu iki eşitlik taraf tarafa çıkarılırsa
|KB| − |KA| = |KD| − |KC| ⇒ |AB| = |CD|
Örnek 6.1. Kesişmeyen ve yarıçap uzunlukları farklı olan iki çemberin
bir ortak dış teğetlerinin değme noktaları A ve B ise |AB| uzunluğunun, çem-
berlerin yarıçap uzunluğu ve merkez noktaları arasındaki uzaklık cinsinden
ifadesi,
7. KUVVET, KUVVET EKSENİ VE KUVVET MERKEZİ
77
M2
M1
A
C
B
Şekil 23
|AB| = |M1 C|
ve
|M2 C| = r2 − r1 olup
△
M1 CM2 dik üçgenine Pisagor teoremi uygulanırsa
|AB|2 = |M1 C|2 = |M1 M2 |2 − |M2 C|2 = d2 − (r2 − r1 )2
(6.10)
⇒ |AB| =
p
(d2 − (r2 − r1 )2
elde edilir.
Örnek 6.2. Yarıçap uzunlukları 3 ve 4 cm olan iki çemberin bir ortak
√
dış teğet parçasının uzunluğu 4 5 cm ise, bu çemberlerin merkez noktaları
arasındaki uzaklık nedir?
Çözüm: 6.10 eşitliğinden
q √
p
√
d = (|AB|2 + (r2 − r1 )2 = (4 5)2 + 1 = 81 = 9 cm dir.
7. KUVVET, KUVVET EKSENİ ve KUVVET MERKEZİ
7.1. Bir Noktanın Bir Çembere Göre Kuvveti. Düzlemde
bir C(M, r) çemberi ve bir A noktası verildiğinde, A noktasından geçen ve
çemberi B ve C noktalarında kesen bir d doğrusu çizelim. Bu durumda
k = |AB||AC| sayısına A noktasının çembere göre kuvveti denir.
d doğrusu değişse bile bir noktanın kuvveti değişmez, yani A noktasından
geçen ve çemberi D ve E noktalarında kesen doğruyu d′ dersek, bu durumda
yine |AD||AE| = k dır.
Gerçekten B ve C noktalarını sırasıyla E ve D noktalarıyla birleştirirsek,
Ĉ ve Ê açıları aynı yayı gören iki çevre açı olduklarından eş açılar ve  açısı
78
5. ÇEMBERLER
C
A
B
M
D
E
Şekil 24. kuvvet
△
△
ortak olduğundan A.A. benzerlik aksiyomuna göre ADC ∼ ABE dir.
⇒
|AC|
|AD|
=
⇒ |AD||AE| = |AB||AC| = k dır.
|AB|
|AE|
* Özel durumlar;
1) Eğer M ∈ d ⇒ k = |AM |2 − r2
2) Eğer B = C = T ⇒ k = |AT |2
3) Eğer A ∈ C(M, r) ⇒ k = 0 dır.
4) Eğer A noktası çemberin iç bölgesinde ise, bu durumda
|AB||AC| = |AD||AE|
E
dir.
B
A
D
C
Şekil 25
İspat: B ve C noktalarını sırasıyla D ve E noktalarıyla birleştirirsek, Ĉ
ve D̂ açıları ile B̂ ve Ê açıları aynı yayı gören iki çevre açı olduklarından eş
△
△
açılardır. A.A. benzerlik aksiyomuna göre ABD ∼ AEC dir.
⇒
|AB|
|AD|
=
⇒ |AB||AC| = |AD||AE| elde edilir.
|AE|
|AC|
7. KUVVET, KUVVET EKSENİ VE KUVVET MERKEZİ
79
7.2. İki Çemberin Kuvvet Ekseni. Aynı düzlemde yatan iki çember
verildiğinde, bu iki çembere aynı kuvvette olan noktaların kümesi bir doğru
gösterir. Bu doğruya bu iki çemberin kuvvet ekseni denir.
A
H
M1 r 1
r2
O
M2
Şekil 26. Kuvvet ekseni
Verilen iki çemberin kuvvet ekseni aşağıdaki şekilde bulunur. Bu iki
çembere göre aynı kuvvette olan bir A noktası alalım. [M1 M2 ] nın orta
noktasına O diyelim. A noktasının [M1 M2 ] sı üzerindeki dikme ayağı H
olsun. Bu durumda
|AM1 |2 − r12 = |AM2 |2 − r22
△
⇔
|AM2 |2 − |AM1 |2 = r22 − r12
△
yazılabilir. AM2 H ve AM1 H dik üçgenlerine Pisagor teoremi uygulanırsa,
|AM2 |2 = |AH|2 + |HM2 |2 ve
|AM1 |2 = |AH|2 + |HM1 |2 elde edilir.
Bu iki eşitlik taraf tarafa çıkarılır ve O noktasının orta nokta olduğu
dikkate alınırsa,
|AM2 |2 − |AM1 |2 = |HM2 |2 − |HM1 |2
= (|HO| + |OM2 |)2 − (|M1 O| − |OH|)2
= |HO|2 + 2|HO||OM2 | + |OM2 |2 − |M1 O|2 + 2|M1 O||OH| − |OH|2
= 2|HO||M1 M2 | = r22 − r12
⇒ |OH| =
r22 − r12
= sbt
2|M1 M2 |
80
5. ÇEMBERLER
⇒ H ∈ [M1 M2 ] sabit nokta olup AH- doğrusu bu iki çemberin kuvvet
eksenidir.
KUVVET EKSENİN ÖZELİKLERİ:
A
K
B
H
M1 r 1
C
E
L
O
r2
M2
D
Şekil 27. Kuvvet ekseninin özelikleri
1) Kuvvet ekseni merkezleri birleştiren doğruya diktir, AH ⊥ M1 M2
2) Kuvvet ekseni ortak teğet parçalarının orta noktasından geçer,
|BK| = |KC|
ve
|DL| = |LE|
3) Teğet çemberlerin kuvvet ekseni, çemberlerin ortak teğetidir.
M1
M2
M1
M2
Şekil 28
4) Kesişen iki çemberin kuvvet ekseni, ortak kirişi taşıyan doğrudur.
5) kuvvet ekseni yarıçapı küçük olan çemberin merkezine daha yakındır.
Örnek 7.1. Çemberin bir [AB]−kirişi üzerinde |AP | = 4 ve |P B| = 9
cm olan bir P noktasından geçen en kısa kirişin uzunluğu nedir?
P noktasından geçen en kısa kiriş, P den geçen çapa dik olan kiriştir.
7. KUVVET, KUVVET EKSENİ VE KUVVET MERKEZİ
81
A
M1
M2
B
Şekil 29
M
P
Şekil 30
7.3. Kuvvet Merkezi. Merkez noktaları doğrusal olmayan üç çembere
göre aynı kuvvette olan noktaya, bu çemberlerin kuvvet merkezi denir. Bu
nokta, merkezleri doğrusal olmayan üç çemberin, ikişer ikişer kuvvet eksenlerinin kesişim noktasıdır.
K
Şekil 31
82
5. ÇEMBERLER
Kuvvet merkezi yardımıyla kesişmeyen iki çemberin kuvvet ekseni aşağıdaki şekilde bulunur.
M1
M2
M
Şekil 32
C(M1 , r1 ) ve C̃(M2 , r2 ) kesişmeyen iki çember olmak üzere, bu iki çemberi kesen üçüncü bir çember çizelim. Kesişim noktalarını A, B, C, D ve
[AB] ∩ [CD] = K dersek K noktası bu üç çemberin kuvvet merkezidir.
Dolayısıyla K noktasından geçen ve [M1 M2 ] doğru parçasına dik olan doğru
bize verilen iki çemberin kuvvet eksenidir.
8. ÇOKGENLER VE ÇEMBERLER
83
8. ÇOKGENLER ve ÇEMBERLER
Bir çokgen ve bir çemberi birlikte ele aldığımız zaman ortak özeliklere
sahip olan bazı yeni kavramlarla karşılaşırız.
8.1. Üçgen ve Çember. Bu iki kavramı birlikte ele aldığımızda karşımıza
çıkan yeni kavramlar şunlardır;
△
8.1.1. İç Teğet Çember. Bir ABC ninin iç bölgesinde, üçgenin kenarlarına
teğet olan çembere o üçgenin iç teğet çemberi denir.
A
M
r
B
Şekil 33. İç Teğet Çember
C
- İÇ TEĞET ÇEMBERİN ÖZELİKLERİ;
1) Her üçgenin bir tek iç teğet çemberi vardır,
2) Üçgenin kenar doğruları, çemberin teğetleridir,
3) Merkez nokta, üçgenin açıortaylarının kesişim noktasıdır,
4) Yarıçap, bu noktanın kenarlara olan uzaklığıdır.
8.1.2. Dış Teğet Çember. Bir üçgenin bir kenarına ve diğer iki kenarın
uzantılarına teğet olan çembere üçgenin dış teğet çemberi denir.
A
M
B
C
Şekil 34. Dış teğet çember
84
5. ÇEMBERLER
- DİŞ TEĞET ÇEMBERİN ÖZELİKLERİ;
1) Her üçgenin üç tane dış teğet çemberi vardır,
2) Üçgenin kenar doğruları, çemberin teğetleridir,
3) Merkez nokta, bir iç ve iki dış açının açıortaylarının kesişim noktasıdır,
4) Yarıçap, bu noktanın teğet olan kenara olan uzaklığıdır.
8.1.3. Çevrel Çember. Bir üçgenin köşe noktalarından geçen çembere o
üçgenin çevrel çemberi denir.
F
A
c
b
ha
B
M
C
H
E
D
Şekil 35. Dış teğet çember
- ÇEVREL ÇEMBERİN ÖZELİKLERİ;
1) Her üçgenin bir tek çevrel çemberi vardır,
2) Üçgenin kenarı, çemberin kirişleridir,
3) Merkez nokta, üçgenin kenar orta dikmelerinin kesişim noktasıdır,
4) Yarıçap, bu noktanın köşe noktalarına olan uzaklığıdır,
5) Herhangi bir açıortay ile karşı kenara ait kenar orta dikme çember
üzerinde kesişir,[AD]−iç açıortay, [AF ]−dış açıortay ve [DF ], a-kenarına ait
orta dikme olup, D, F ∈ C(M, r) dir.
8. ÇOKGENLER VE ÇEMBERLER
6) Yarıçap uzunluğu r =
İspat 6:
85
bc
dır.
2ha

△
△
B̂ ∼
= Ê 
|AB|
|AH|
c
ha
bc
⇒ ABH ∼ AEC ⇒
=
⇒
=
⇒r=

|AE|
|AC|
2r
b
2h
∼
a
Ĥ = Ĉ
8.2. Dörtgenler ve Çemberler.
8.2.1. Teğetler Dörtgeni. Bütün kenarları bir çembere teğet olan dörtgene teğetler dörtgeni denir.
D
c
d
C
M
b
a
A
B
Şekil 36. Teğerler dörtgeni
-TEĞETLER DÖRTGENİNİN ÖZELİKLERİ;
1) İç açıortaylarının kesim noktası, çemberin merkezidir,
2) Karşılıklı kenar uzunluklarının toplamı birbirine eşittir, a + c = b + d
8.2.2. Kirişler Dörtgeni. Kenarları bir çembere kiriş olan dörtgene kirişler dörtgeni denir.
D
d
A
c
M
a
C
b
B
Şekil 37. Kirişler dörtgeni
86
5. ÇEMBERLER
KİRİŞLER DÖRTGENİNİN ÖZELİKLERİ;
1) Karşılıklı açıları bütünlerdir.
m(Â) + m(Ĉ) = m(B̂) + m(D̂) = 180o
1 \
1 \
+ m(BAD)
İspat: m(Â) + m(Ĉ) = m(DCB)
2
2
1
\ + m(BAD))
\ = 1 3600 = 180o
= (m(DCB)
2
2
elde edilir.
9. GEOMETRİK YER KAVRAMI ve BELİRLENMESİ
Tanım 5.4. Verilen bir veya birkaç şartı sağlayan noktaların kümesine,
o noktaların geometrik yeri denir.
Bu tanıma göre;
1) Geometrik yere ait olan her nokta verilen şartları sağlar,
2) Verilen şartları sağlayan her nokta geometrik yere aittir.
Örnek 9.1.
Düzlemde sabit bir M noktasından r − br uzaklıktaki noktaların kümesi
(geometrik yeri) C(M, r) çemberdir.
A
r
Y
D
M
X
B
Şekil 38. Geometrik yer
|AM | = |BM | = r br olduğundan A, B ∈ C(M, r)
|XM | < r ve |Y M | > r olduğundan X, Y ∈ C(M, r)
9. GEOMETRİK YER KAVRAMI VE BELİRLENMESİ
87
Örnek 9.2.
Düzlemde verilen iki noktaya eşit uzaklıktaki noktaların kümesi (geometrik yeri) bu noktaların oluşturduğu doğru parçasının orta dikmesi olan
doğrudur.
A
d
B
D
Şekil 39. orta dikme
Örnek 9.3.
Düzlemde verilen bir d doğrusundan sabit (h − br) uzaklıktaki noktaların
kümesi verilen doğrunun farklı taraflarında paralel iki doğrudur.
h
d
h
D
Şekil 40. paralel doğrular
Örnek 9.4.
Düzlemde verilen iki noktaya (F1 , F2 ) uzaklıkları toplamı sabit olan noktaların geometrik yeri nedir?
Düzlemde verilen iki nokta bir doğru parçası belirtir ve her doğru parçasının
bir orta noktası vardır. [F1 F2 ] nın orta noktası O ve |OF | = c diyelim. a > c
88
5. ÇEMBERLER
bir sabit sayı olmak üzere |P F1 | + |P F2 | = 2a eşitliğini sağlayan P ∈ E nok√
talarının kümesi O−mekezli, yarı eksen uzunlukları a ve b = a2 − c2 olan
bir elipsdir.
P B
O
F1
F2
A
Şekil 41. Elips
Örnek 9.5.
\ açısının kenarlarına eşit uzaklıktaki noktaların kümesi, bu
Bir ABC
açının açıortayı olan ışındır.
C
d
A
D
B
Şekil 42. açıortayı
Örnek 9.6.
Bir [AB] doğru parçasını sabit bir α (0 < α < 90o ) açısıyla gören noktaların kümesi, bu doğru parçasını ortak kiriş kabul eden iki çember yayıdır.
Bu doğru parçasının uç noktaları bu geometrik yere ait değildir.
[AB] doğru parçası ve α açısı verildiğinde bu çember yayları aşağıdaki
şekilde bulunur.
ˆ
m(BAX)
= α olacak şekilde bir [AX ışını alalım. A noktasında bu
ışına dik olan doğrunun, [AB] doğru parçasının orta dikmesiyle kesişim noktası M olmak üzere, M noktasını merkez ve |AM | = |BM | = r uzaklığını
9. GEOMETRİK YER KAVRAMI VE BELİRLENMESİ
89
C
M
A
B
X
D
Şekil 43. Geometrik yer
yarıçap kabul eden çemberin büyük olan yayı üzerindeki her noktanın A ve
B noktalarıyla oluşturdu açının ölçüsü α dır. Gerçekten,
ˆ
ˆ ) = 90o − α
[M A] ⊥ [AX ve m(XAB)
= α ⇒ m(BAM
ˆ
BAC−
açısı çapı gören çevre açı olduğundan
△
ˆ
ˆ )=α
m(BAC)
= 90o ⇒ m(CAM
M CA ikizkenar üçgen olup taban açıları eş olduğundan
ˆ
m(ACB)
= α dır.
\ yayı üzerindeki her
Aynı yayı gören çevre açılar eş olduğundan ACB
noktanın A ve B noktalarıyla birleştirilmesiyle oluşan açının ölçüsü sabit ve
α dır.
Ayrıca M noktasının [AB] doğru parçasına göre simetriği olan M ′ noktasını merkez ve |AM ′ | = |BM ′ | = r uzaklığını yarıçap kabul eden çemberin
büyük olan yayı üzerindeki her noktanın A ve B noktalarıyla oluşturdu açının
ölçüsü de α dır. O halde bu iki çember yayı yukarıdaki şartları sağlayan iki
yaydır.
Soru: Uzunluğu 2 cm olan bir [AB] doğru parçasını 30o lik açı ile gören
noktaların geometrik yerini bulunuz.
BÖLÜM 6
ALAN HESABI
Çokgensel bölgenin, bir çokgen ile iç bölgesinin birleşim kümesi olduğunu
biliyoruz, fakat söylemindeki kolaylık nedeniyle çokgensel bölgenin alanı yerine çokgenin alanı ifadesini kullanacağız. Her doğru parçasına ve her açıya
bir pozitif reel sayı karşılık geldiği gibi her bir çokgensel bölgeye de bir pozitif reel sayı karşılık gelir. Bu sayıya o bölgenin alanı denir. Her ölçüm bir
birime göre yapılır. Alan ölçüsünün birimi, bir kenarının uzunluğu 1 birim
olan karenin düzlemde kapladığı alan olarak alınır ve 1 br2 ile gösterilir.
br2
1 br
1 br
Şekil 1. birimkare
Bir çokgensel bölge öyle sonlu sayıda alt bölgelere ayrılabilir ki bu bölgelerin alanlarının toplamı esas bölgenin alanını verir.
Bir çokgenin alan hesabında kullanılan bazı temel kavramlar vardır. Bunlar taban ve yükseklik kavramlarıdır. Bir üçgende herhangi bir kenar taban
olarak alınabilir. Bir ucu taban doğrusu üzerinde, tabana dik ve diğer ucu
taban olarak alınan kenara karşılık gelen köşe noktası olan doğru parçasının
uzunluğuna o kenara ait yükseklik denir.
|AH| = ha
a-kenarına ait yüksekliktir.
90
1. ÇOKGENSEL BÖLGELERİN ALANI
91
A
b
c
ha
B
a
H
C
Şekil 2. Üçgende yükseklik
C
D
hb
ha
A
b
a
H
B
Şekil 3. Paralel kenarda yükseklik
Bu hazırlıklardan sonra çokgenlerde alan hesaplarına geçebiliriz.
1. ÇOKGENSEL BÖLGELERİN ALANI
1.1. Karenin Alanı. Kenar uzunluğu a br olan karenin alanı
s(ABCD) = a2 br2 dir.
1.2. Dikdörtgenin Alanı. Bir ABCD dikdörtgeninde bitişik iki kenardan biri diğerine ait yükseklik olduğundan alan
s(ABCD) = a × b br2 dir.
D
C
D
a
b
a × b br2
a2 br2
A
C
B
A
a
Şekil 4. Kare ve Dikdörtgenin Alanı
B
92
6. ALAN HESABI
△
1.3. Dik Üçgenin Alanı. Bir ABC dik üçgeni aşağıdaki şekilde bir
△
△
ABCD dikdörtgenin tamamladığımızda elde edilen ABC ve CDA üçgenleri
eş üçgenler olup alanları toplamı dikdörtgenin alanına eşittir. Buna göre
üçgenin alanı,
A
D
c
a
B
C
Şekil 5. Dik üçgenin alanı
△
a×c
1
br2 dir.
s(ABC) = s(ABCD) =
2
2
Sonuç 6.1. Bir dik üçgenin alanı, dik kenar uzunlukları çarpımının
yarısına eşittir.
△
1.4. Üçgenin Alanı. Bir ABC üçgeni verildiğinde bu üçgeni aşağıdaki
şekilde bir BCDE dikdörtgenine tamamlayabiliriz. Buna göre üçgenin alanı,
E
D
A
K
ha
c
B
a
F
C
Şekil 6. Üçgenin Alanı
△
△
△
s(ABC) = s(BCDE) − s(AEB) − s(ACD)
|AE|.|EB| |AD|.|DC|
−
2
2
a.ha
a.ha
2
=
br
= a.ha −
2
2
=b×c−
1. ÇOKGENSEL BÖLGELERİN ALANI
93
elde edilir. Böylece aşağıdaki sonuçları verebiliriz,
Sonuç 6.2.
1) Bir üçgenin alanı, bir kenar uzunluğu ile bu kenara ait yüksekliğinin
çarpımın yarısına eşittir.
2) Bir üçgende bir kenarortay, üçgeni alanları eşit iki üçgene ayırır, yani
△
ABC üçgeninde [AF ], a− kenarına ait kenarortay ise
△
△
s(ABF ) = s(AF C)
3) Aynı yüksekliğe sahip iki üçgenin alanlarının oranı, bu yüksekliklerin
ait olduğu kenarların uzunlukları oranına eşittir, yani
△
s(ABF )
△
=
|BF |
|F C|
s(AF C)
4) Bir üçgenin bir açı ortayının oluşturduğu iki üçgenin alanlarının oranı,
bu açıyı oluşturan kenarların uzunlukları oranına eşittir, yani
△
s(ABK)
△
s(BKC)
=
|BA|
|BC|
5) Bir kenarının uzunluğu a br olan eşkenar üçgenin alanı
√
3 2
a dir.
4
İspat 5: Eşkenar üçgen aynı zamanda bir ikizkenar üçgen olduğundan
taban ait yükseklik hem kenarortay hem de açıortaydır.
△
a
|BH| = |HC| = ve m(Ĥ) = 90o olup ABH dik üçgeninde P.T. den
2
√
3 2
a2
3
2
2
2
2
= a ⇒ ha =
a
|AH| = |AB| − |BH| = a −
4
4
2
√
△
3 2 2
a.ha
⇒ s(ABC) =
=
a br dir.
2
4
94
6. ALAN HESABI
A
a
B
H
a
2
C
Şekil 7. Eşkenar Üçgenin Alanı
1.5. Paralel Kenarın Alanı. Bir ABCD paralel kenarında
D
C
c=a
ha
A
a
H
B
Şekil 8. Paralel kenarın Alanı
a−kenarına ait yükseklik ha olmak üzere
△
△
s(ABCD) = s(ABD) + s(DBC)
=
a.ha a.ha
+
= a.ha br2
2
2
Sonuç 6.3. Bir paralel kenarın alanı, bir kenar uzunluğu ile o kenara ait
yüksekliğin çarpımına eşittir.
1.6. Yamuğun Alanı.
△
△
s(ABCD) = s(ABD) + s(DBC)
=
a.ha c.ha
(a + c).ha
+
=
br2
2
2
2
Sonuç 6.4. Bir yamuğun alanı, taban uzunluklarının toplamı ile yüksekliğinin çarpımının yarısına eşittir.
1. ÇOKGENSEL BÖLGELERİN ALANI
D
95
C
c
ha
A
H
a
B
Şekil 9. Yamuğun Alanı
D
H
A
C
B
Şekil 10. Deltoidin Alanı
1.7. Deltoidin Alanı.
△
△
s(ABCD) = s(ABD) + s(DBC)
=
|BD||AC|
|BD||AH| |BD||HC|
+
=
br2
2
2
2
Sonuç 6.5. Bir deltoidin alanı,köşegen uzunluklarının çarpımının çarpımının
yarısına eşittir.
1.8. Düzgün Çokgenlerin Alanı. Düzgün çokgenlerin kenar uzunlukları eşit ve açıları eştir. Her düzgün çokgenin köşeleri bir çember üzerindedir. Bu çembere düzgün çokgenin çevrel çemberi denir.
Her düzgün çokgenin bir içteğet çemberi vardır. Buna göre aşağıdaki
tanımları verebiliriz.
Tanım 6.1. n-kenarlı bir düzgün çokgen verildiğinde,
96
6. ALAN HESABI
r
M
h
Şekil 11. Düzgün çokgen
1) Çevrel çemberin ve iç teğet çemberin ortak olan merkezine, düzgün
çokgenin merkezi denir, M merkez noktadır.
2) Çevrel çemberin yarıçapına düzgün çokgenin yarıçapı denir, r−yarıçapdır.
3) İçteğet çemberin yarıçapına düzgün çokgenin apotemi denir, h− apotemidir.
4) Bir kenarı gören merkez açıya düzgün çokgenin merkez açısı denir.
Bir kenarının uzunluğu a−br olan n-kenarlı bir düzgün çokgen (Pn ) olmak üzere C(Pn ) = n.a dır.
(Pn ), M noktası ortak köşe olmak üzere, n-tane eş ikizkenar üçgene
ayrılır.
△
△
△
M P1 P2 ∼
= ... ∼
= M Pn P1
= M P2 P3 ∼
△
△
△
△
(Pn ) = M P1 P2 ∪ M P2 P3 ∪ ... ∪ M Pn P1
s(M Pi Pi+1 ) =
a.h
a.h
C(Pn ).h
⇒ s(Pn ) = n.
=
elde edilir.
2
2
2
Sonuç 6.6. Bir düzgün çokgenin alanı, çevre uzunluğu ile apoteminin
çarpımının yarısıdır.
2. DAİRESEL BÖLGELERİN ALANI
97
2. DAİRESEL BÖLGELERİN ALANI
2.1. Dairenin Alanı. r−yarıçaplı bir daire verildiğinde alanı aşağıdaki
şekilde hesaplanır. Bu dairenin içine n-kenarlı bir düzgün çokgen çizildiğinde
M
h
r
Şekil 12. Daire
C(Pn ).h
eşitliği ile hesaplandığını
2
biliyoruz. Burada n −→ ∞ için çokgenin çembere, bölgenin de daireye
bu düzgün çokgenin alanının s(Pn ) =
dönüştüğü söylemiştik. O halde bu düzgün çokgenin alanı da dairenin alanı
olacaktır. Buna göre,
n −→ ∞ için (Pn ) −→ Dr
C(Pn ) −→ 2πr
ve
h −→ r dönüşür,
bu değerler yerine yazılırsa, dairenin alanı için,
s(Dr ) =
2πr2
= πr2 br2 elde edilir.
2
Sonuç 6.7. r−yarıçaplı dairenin alanı s(Dr ) = πr2 br2 dir.
2.2. Daire Diliminin Alanı. r− yarıçaplı bir dairede iki yarıçap ve
bu yarıçapların belirttiği yay ile sınırlanan bölgeye daire dilimi denir.
Merkez açısının ölçüsü α olan bir daire diliminin alanı
(2.1)
dir.
s(Dd (α)) =
α
.πr2 br2
360
98
6. ALAN HESABI
M
α
Şekil 13. Daire dilimi
2.3. Daire Parçasının Alanı. Bir [AB]−kirişi ve bu kirişin çemberden
ayırdığı yayın sınırladığı bölgeye daire parçası denir.
[AB]−kirişini gören merkez
açının ölçüsü α olan bir daire
parçasının alanı, aynı merkez
M
açıya sahip daire diliminin
α
alanından M AB nin alanı
△
çıkarılarak bulunur.
A
(2.2)
B
Buna
göre
△
s(Dp (α)) = s(Dd (α)) − s(M AB) = (
α
r2 .sinα
.πr2 −
) br2
360
2
dir. Burada,
sin α =
|AH|
⇒ |AH| = r sin α,
r
△
s(M AB) =
|AH||M B|
r2 .sinα
=
br2
2
2
Örnek 2.1. Bir kenarının uzunluğu 8 cm olan karenin bitişik iki kenarını
çap kabul eden iki çember yaylarının sınırladığı bölgenin alanını bulunuz.
Çözüm:
2. DAİRESEL BÖLGELERİN ALANI
99
C
x
A
H
B
Şekil 14
s(A) = 2x
△
x = s(D90o ) − s(M HB) = πr2
⇒ s(A) = 2x = 16(
sin 90 2 16
16
π
90
−
r =
π−
= 8( − 1)
360
2
4
2
2
π
− 1)
2
2.4. Halkanın Alanı. Merkezleri aynı yarıçap uzunlukları farklı olan
iki çember arasında kalan bölgeye halka denir.
M
r2
Bir halkanın alanı,
büyük
dairenin
küçük
dairenin
r1
alanından,
alanı
bulunur. Buna göre halkanın
alanı,
(2.3)
dir.
çıkarılarak
s(H(r1 , r2 )) = π.r22 − π.r12 = π(r22 − r12 ) br2
100
6. ALAN HESABI
Sonuç 6.8. Bir düzgün çokgenin, çevrel çemberi ile iç teğet çemberi
arasında kalan halkanın alanı, bu düzgün çokgenin bir kenar uzunluğunun
yarısının karesi ile π nin çarpımına eşittir, yani
s(H(h, r)) = π(r2 − h2 ) = π( a2 )2 br2
Örnek 2.2. Bir kenarının uzunluğu 4 − cm olan n−kenarlı bir düzgün
çokgenin iç teğet ve çevrel çemberleri arasındaki alan nedir?
Çözüm:
S(A) = π( a2 )2 = π( 42 )2 = 4π br2
Örnek 2.3. Yarıçap uzunlukları eş ve 2 cm olan üç çember birbirine
dıştan teğet olduğuna göre bu çemberler arasında kalan bölgenin alanı nedir?
M1
M2
M3
Şekil 15
İstenen alan, bir kenarının uzunluğu a = 4 cm olan bir eşkenar üçgenin
alanından merkez açısı α = 60o olan 3 daire dilimin alanın frakına eşittir.
Buna göere istenen alan,
A=
√
√
√
3 2
60
4 − 3π22
= 4 3 − 2π = 2( 3 − π) br2
4
360
BÖLÜM 7
KATI CİSİMLERİN ALAN ve HACİM
HESAPLARI
Katı cisimlerin alan ve hacimlerini daha kolay hesaplayabilmek için cisimlerin görünüşlerine göre bazı sınıflandırmalar yapılabilir. Bu sınıflandırmalar,
prizmalar, piramitler, silindir, koni ve küre vs ...
1. PRİZMALAR
Tanım 7.1. Bir düzlemde verilen bir (Pn ) çokgensel bölgenin kendine
paralel kalacak şekilde derinliğine hareket ettirilmesiyle oluşan cisme prizma
denir.
△
Mesela (Pn ) ←→ ABC alındığında, aşağıdaki prizma elde edilir.
Ȧ
Ḣ
Ḃ
Ė
Ċ
Ä
h
B̈
C̈
A
B
C
H
E
Şekil 1. Prizma
* Prizmayla İlgili Tanımlar ve Çıkarılan Sonuçlar
Bir (Pn )− çokgensel bölgeden elde edilen prizma için,
101
102
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
△
• (Pn )−çokgensel bölgeye prizmanın alt tabanı ∼ tabanı denir, ABC
üçgeni tabandır,
• prizmalar tabanı oluşturan çokgenlerin kenar sayısına göre isimlendirir-
ler, üçgen prizma, dörtgen prizma vs...
△
• (Ṗn )−çokgensel bölgeye prizmanın üst tabanı ∼ tavanı denir, ȦḂ Ċ
• E ve Ė düzlemleri arasındaki uzaklığa |H Ḣ| = h, prizmanın yüksekliği
denir,
• [Pi Ṗi ]−doğru parçalarına prizmanın yan ayrıtları denir,
• ardışık iki yan ayrıt arasında kalan bölgelere ( ki bunlar birer parlel
kenardır) Pi Pi+1 Ṗi+1 Ṗi , prizmanın yan yüzleri denir,
• bir prizmanın tabanına paralel bir düzlemle arakesitine, prizmanın
△
enine kesiti denir, ÄB̈ C̈
Sonuç 7.1. Bir prizmada taban, tavan ve her bir enine kesit eştir,
△
△
△
ABC ∼
= ȦḂ Ċ ∼
= ÄB̈ C̈
Teorem 7.1. Bir prizmanın yüzeyinin alanı taban alan, tavan alanı ve
yan yüzlerin alanlarının toplamına eşittir.
S(P ) = s(Pn ) + s(Ṗn ) +
n
X
s(Pi Pi+1 Ṗi+1 Ṗi )
i=1
(1.1)
= 2s(Pn ) +
n
X
i=1
|Pi Pi+1 | × h
= 2s(Pn ) + C(Pn ) × h
Sonuç 7.2. Bir prizmanın yanal alanı, tabanın çevresi ile yüksekliğinin
çarpımına eştir,
(1.2)
s(Ya ) = C(Pn ) × h
1. PRİZMALAR
103
Sonuç 7.3. Bir prizmanın hacmi, taban alanı ile yüksekliğinin çarpımına
eştir,
(1.3)
V (P ) = S(Pn ) × h
• m(Pi Pˆi X) = α, X ∈ E olmak üzere α = 90o ise, prizmaya dik prizma,
aksi halde eğik prizma denir,
• bir dik prizmanın yan yüzleri birer dik dörtgen dir,
• bir dik prizmanın yan ayrıtlarının uzunlukları prizmanın yüksekliğine
eşittir, yani her i-için h = |Pi Ṗi |
Ṗi
h
α
Pi
Pi+1
Şekil 2. dik prizma
• bir prizmada K= köşe sayısı, Y= yüz sayısı ve A= ayrıt sayısı olmak
üzere, bunlar arasında K + Y − A = 2 eşitliği geçerlidir, bu eşitliğe Euler
bağıntısı denir.
Mesela bir üçgen prizma için, 6 + 5 − 9 = 2 dir.
• dik dörtgen prizmada yüzlerin köşegenine yüz köşegeni, aynı yüzde
olmayan iki köşeği birleştiren doğru parçasına da cisim köşegeni denir.
[ȦB]− yüz köşegeni ve [ȦC]−cisim köşegenidir. Bu köşegenlerin uzunluklarını cismin boyutları cinsinden hesaplanabilir,
104
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
Ċ
Ḋ
Ȧ
Ḃ
D
C
A
B
Şekil 3. Dörtgen Prizma
|ȦB| =
√
ve
a2 + h2 br
|ȦC| =
√
a2 + b2 + h2 br dir.
Tanım 7.2. Bütün ayrıtları eş olan dikdörtgen prizmaya küp denir.
Ċ
Ḋ
Ȧ
Ḃ
D
A
C
B
Şekil 4. küp
Sonuç 7.4. Bir ayrıtının uzunluğu a br olan bir küpün için a = b = h
olduğundan
• her bir yüz köşegeninin uzunluğu |ȦB| =
√
2a br
√
• her bir cisim köşegeninin uzunluğu |ȦC| = 3a br dir.
2. PİRAMİTLER
105
2. PİRAMİTLER
Tanım 7.3. Bir E−düzleminde bir (Pn ) çokgeni ile bu düzlemde olmayan bir T noktası verildiğinde [T P1 ]− doğru parçasının çokgenin kenarları
boyunca hareket ettirilmesiyle oluşan cisme tepe noktası T olan piramit denir
ve (T, Pn ) ile gösterilir.
Mesela (Pn ) ←→ ABCD alındığında
T
h
D
C
H
A
Hi
B
Şekil 5. Piramit
⋆ T noktasına piramidin tepe noktası denir,
⋆ (Pn ) çokgensel bölgeye piramidin tabanı denir, ABCD dörtgeni tabandır,
⋆ [T Pi ]− doğru parçalarına piramidin yan ayrıtları denir,
⋆ T noktasının E düzlemine olan uzaklığına |T H| = h, piramidin yük-
sekliği denir,
△
⋆ T Pi Pi+1 üçgenlerine piramidin yan yüzleri denir,
⋆ |T Hi | = hi uzaklıklarına i-yinci yüze ait yükseklik denir,
⋆ piramitlerde prizmalar gibi tabanı oluşturan çokgenlerin kenar sayısına
göre isimlendirilirler, üçgen piramit, dörtgen piramit vs...
Teorem 7.2. Bir piramidin alanı, taban alanı ile yan yüzlerin alanları
toplamına eşittir,
106
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
S(T, P ) = s(Pn ) +
(2.4)
= s(Pn ) +
n
X
i=1
n
X
i=1
△
s(T Pi Pi+1 )
|Pi Pi+1 | × hi
2
Tanım 7.4. Tabanı düzgün çokgen ve yükseklik ayağı tabanın merkezi
olan piramide düzgün piramit denir, yani bir düzgün piramitte yükseklik ayağı
G ve h = |T G| dir,
⋆ bir düzgün piramidin yan yüzleri eş ikizkenar üçgenlerdir,
⋆ yan ayrıtların uzunlukları eşittir,
⋆ yan yükseklikler eşittir,
Sonuç 7.5. Bir kenarının uzunluğu a − br olan düzgün piramidin alanı,
(2.5)
S(T, P ) =
n.a.h
2
Teorem 7.3. Bir piramit tabanına paralel bir düzlemle kesildiğinde
i ) kesit çokgeni tabana benzerdir, Ṗn ∼ Pn
Şekil 6. Kesit
2. PİRAMİTLER
107
ii ) kesit çokgeninin alanının taban alanına oranı, bunların tepe noktasına
olan uzaklıklarının oranının karesine eşittir,
|T H ′ | 2
s(Ṗn )
=(
)
s(Pn )
|T H|
(2.6)
İspat: Tales teoreminin bir sonucudur.
Teorem 7.4. (Cavalier Prensibi): Taban alanları ve yükseklikleri eşit
olan iki cismin tabanlarına aynı uzaklıktaki paralel kesitlerinin alanları eşit
ise bu iki cismin hacimleri de eşittir.
Sonuç 7.6. Taban alanları ve yükseklikleri eşit olan piramitlerin hacimleri de eşittir.
Teorem 7.5. Bir piramidin hacmi, taban alanıyla yüksekliği çarpımının
üçte birine eşittir, yani
(2.7)
V (T, Pn ) =
1
S(Pn ) × h
3
İspat: Bu teoremi iki adımda ispatlayabiliriz.
I.Adım: Herhangi bir (T, ABC)− üçgen piramidi verilsin. Bu piramidi
aşağıdaki şekilde bir (ABCET D)− üçgen prizmaya tamamlayalım.
Bu prizma (A, D, T )− düzlemiyle kesildiğinde elde edilen (A, T DE)−üçgen
piramidi tabanları ve yükseklikleri eşit olduğundan bize verilen (T, ABC)−piramidine
eştir,
(2.8)
(A, T DE) ∼
= (T, ABC)
ve prizmanın bu piramitle farkı (A, T BCD)−dörtgen piramididir. Ayrıca
(2.9)
(A, T BCD) = (A, T BC) ∪ (A, T CD) = (T, ABC) ∪ (A, T CD)
⇒ (T, ABC) ∼
= (A, T DE) ∼
= (A, T CD) olup
108
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
E
D
T
C
A
B
Şekil 7
(T, ABC) ∪ (A, T DE) ∪ (A, T CD) = (ABCET D) olduğundan
△
3 × V (T, ABC) = V (ABCT DE) = s(ABC) × h
⇒ V (T, ABC) =
△
1
s(ABC) × h
3
II.Adım: Herhangi bir (T, Pn ) piramidi verildiğinde P1 noktasının sırasıyla
P3 , P4 , ..., Pn−1 noktalarıyla oluşturduğu köşegenlerin T noktasıyla belirttiği
düzlemler verilen piramidi (n − 2)−üçgen piramide ayırır ve bunların birleşimi esas piramidi oluşturur. O halde
△
△
△
V (T, Pn ) = V (T, P1 P2 P3 ) + V (T, P1 P3 P4 + ... + V (T, P1 Pn−1 Pn
=
△
△
△
1
1
1
s(P1 P2 P3 )×h+ s(P1 P3 P4 )×h+...+ s(P1 Pn−1 Pn )×h
3
3
3
2. PİRAMİTLER
109
T
Pi
P3
Pn
P1
P2
Şekil 8. Düzgün Piramit
=
△
△
△
h
[s(P1 P2 P3 ) + s(P1 P3 P4 ) + ... + s(P1 Pn−1 Pn )]
3
=
1
S(Pn ) × h
3
elde edilir. n = 4 için
T
D
C
A
B
Şekil 9. Kesit
△
△
V (T, ABCD) = V (T, ABC) + V (T, ACD)
110
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
=
△
△
1
1
s(ABC) × h + s(ACD) × h
3
3
=
△
△
1
[s(ABC) + s(ACD)] × h
3
=
1
1
[s(ABCD)] × h =
Ta × h
3
3
Tanım 7.5. Altı ayrıtıda eş olan piramite düzgün dört yüzlü denir.
T
A
D
A
G
C
G=H
E
D
B
C
E
B
Şekil 10. Düzgün dört yüzlü
Sonuç 7.7. Bir ayrıtının uzunluğu a − br olan düzgün dört yüzlünün,
√
6
a) yüksekliği h = |T G| =
a br
3
b) alanı S(T, ABC) =
√
c) hacmi V (T, ABC) =
dür.
3 a2 br2
√
2 3 3
a br
12
△
İspat: Her ayrıtın uzunluğu a br olduğuna göre, AEC dik üçgeninden
|AE|2
=
a2
√
3
a2
3 2
−
= a ⇒ |AE| =
a br
4
4
2
3. SİLİNDİR
111
√
3
2
a br
|AG| = |AE| =
3
3
|T G|2
=
|T A|2
−
|AG|2
=
a2
√
6
3 2 6 2
− a = a ⇒ h = |T G| =
a br
9
9
3
√
△
√
3 2 2
a br ⇒ S(T, ABC) = 4 × s(ABC) = 3 a2 br2
4
√
√
√
△
3 2
2 3 3
6
1
a ×
a=
a br
⇒ V (T, ABC) = s(ABC) × h =
3
12
3
12
△
s(ABC) =
elde edilir.
3. SİLİNDİR
Bir basit kapalı C ⊂ E eğrisi ve bu düzleme paralel olmayan bir d doğrusu
verildiğinde, d doğrusunun C eğrisine dayanarak kendisine paralel kalacak
şekilde hareket etmesiyle oluşan yüzeye silindirik yüzey denir.
C eğrisine, bu yüzeyin dayanak eğrisi,
d doğrusuna da ana doğrusu veya doğrultman doğrusu denir.
d
A
α
c
l
h
E
⊥
B
Şekil 11. silindir
112
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
Bir silindirik yüzey paralel iki düzlemle kesildiğinde, düzlemlerin yüzeyin
içinde kalan parçaları ve yüzeyin düzlemler arasında kalan parçası ile sınırlanan cisme silindir denir. Bu düzlem parçalarına silindirin tabanı ve tavanı,
yüzey parçasına yanal yüzeyi ve düzlemler arasındaki uzaklığa silindirin
yüksekliği denir.
Silindirler de tabanlarına göre isimler alırlar dairesel silindir, eliptik silindir
vs ...
Tanım 7.6. Ana doğrunun taban düzlemiyle yaptığı açı α, 0 < α < 90o
olmak üzere, elde edilen silindire eğik silindir, α açısına da eğik silindirin
eğim açısı denir. α = 90o ise, elde edilen silindire dik silindir, tabanı daire
olan dik silindire de dik dairesel silindir denir.
Sonuç 7.8. Eğim açısı α olan eğik silindirin
a) Yanal alanı
burada,
Ya = c × l =
c×h
= c × h csc α br2
sin α
c : eğrinin uzunluğunu,
l : ana doğrunun düzlemler arasında kalan parçasının uzunluğunu l = |AB|
göstermektedir.
b) Alanı
Sa = Ya + 2A br2
A : daynak eğrisinin sınırladığı bölgenin alanı,
c) Hacmi
V = A × h = A × l sin α br3 dür.
Sonuç 7.9. r-yarıçaplı dik dairesel silindirin
a) Yanal alanı
b) Alanı
c) Hacmi
dür.
Ya = 2πr × h br2
Sa = Ya + 2πr2 = 2πr(h + r) br2
V = πr2 × h br3
4. KONİ
113
r
Ya = 2πr × h br2
h
2πr
πr2
Şekil 12. D.D.S.Açınımı
Tanım 7.7. Bir dik dairesel silindir, kenar uzunlukları r ve h birim olan
bir dik dörtgenin bir kenarı etrafında 360o döndürülmesiyle de elde edildiğinden bazen dönel silindir olarak ta isimlendirilir.
4. KONİ
Basit kapalı bir C ⊂ E eğrisi ve bu düzlemde olmayan bir T noktası
verildiğinde elde edilen [T P ], P ∈ C doğru parçalarının birleşim kümesine
koni yüzeyi, koni yüzeyi ile C eğrisinin sınırladığı düzlem parçası tarafından
sınırlanan cisme koni denir. T noktasına koninin tepe noktası, [T P ] doğru
parçalarına da ana doğruları denir.
T
T
l
h
P
⊥
H
C
Şekil 13. Koni
r
H
A
114
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
C eğrisinin sırladığı bölgeye koninin tabanı denir. Bir konide tepe noktasının taban düzlemine olan uzaklığına koninin yüksekliği, koninin tepe
noktasını tabanın merkezine birleştiren doğru parçasına konin ekseni denir.
Koniler de taban eğrilerine göre dairesel koni, eliptik koni vs... olarak isimlendirilir.
4.1. Koni Çeşitleri.
4.1.1. Eğik Koni.
Tanım 7.8. Yükseklik ayağı tabanın merkezi olmayan koniye eğik koni
denir.
4.1.2. Dik Dairesel Koni.
Tanım 7.9. Ekseni taban düzlemine dik olan dairesel koniye dik dairesel
koni denir.
△
Dik dairesel koni, bir dik üçgenin (T HA) dik kenarlarından birisi ([T H])
etrafında 360o döndürülmesiyle elde edilebildiğinden bu koniye bazen dönel
koni de denir. T H−doğrusuna dönel koninin (dönme) ekseni denir.
* DİK DAİRESEL KONİNİN ÖZELİKLERİ;
1) Ana doğruları bir birine eştir,
2) Ekseni yüksekliği tanımlayan doğrudur,
3) Ekseni içine alan bir düzlemle kesişimi, bir ikizkenar üçgendir.
Teorem 7.6. r−yarıçaplı bir dik dairesel koni yüzeyinin,
a) Yanal alanı
Ya =
2πr × l
= πr × l br2
2
burada, l : ana doğrunun uzunluğunu l = |T A|
b) Alanı
Sa = Ya + Ta = πr × l + πr2 = πr × (l + r) br2
4. KONİ
c) Hacmi
115
1
V = πr2 × h br3 dür.
3
T
Ya
a
h
r
H
A
Şekil 14. Koninin yanal alanı
Bu koniye taban kenarının sayısı sonsuz olan bir düzgün piramit olarak
ele alıp, piramitler için ifade edilen önermeleri koni için de kullanabiliriz.
4.1.3. Kesik Koni.
Tanım 7.10. Bir dönel koni, tabana paralel bir düzlemle kesildiğinde, bu
düzlemle taban düzlemi arasında kalan parçasına kesik koni denir.
T
h2
l
l2
A′
H′
l1
h1
r
H
A
Şekil 15. Kesik koni
Teorem 7.7. Yarıçapları r ve r′ , yüksekliği h olan bir dik dairesel kesik
koninin,
116
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
a) yanal alanı, taban ve tavanın çevreleri toplamı ile ana doğru parçasının
uzunluğu çarpımının yarısına eşittir, yani l1 = |AA′ | ve l2 = l − l1 olmak
üzere
Ya = π(r + r′ ) × l1 br2
(4.10)
b) hacmi,
1
V = π.h1 (r2 + r′2 + r.r′ ) br3
3
(4.11)
dür.
△
△
İspat: A.A.A benzerlik teoremine göre T H ′ A′ ∼ T HA olduğundan
(4.12)





r′
h2
l2
=
=
⇒

h
r
l



h = h1 + h2
ve
r′ .l = r.l2 ⇒ π.r′ .l = π.r.l2

 r′2 h = rr′ h
2
r′ .h = r.h2 ⇒
 rr′ h = r2 h2
l = l1 + l2
olduğu göz önüne alınırsa,
Ya = πr.l − πr′ .l2 = πr.l + πr′ .l − πr.l2 − πr′ .l2
= π(r + r1 ).l − π(r + r1 ).l2
= π(r + r′ ).(l − l2 ) = π(r + r2).l1 br2
b) kesik koni şekil 15 de verilen iki koninin farkı olrak düşünülürse hacmi,
1
1
V = πr2 .h − πr′2 .h2
3
3
1
= π[r2 .h+r′2 h − rr′ h2 + rr′ h − r2 h2 − r′2 .h2 ]
3
1
= π[r2 (h − h2 ) + r′2 (h − h2 ) + rr′ (h − h2 )]
3
1
= π.h1 (r2 + r′2 + rr′ ) br3 elde edilir.
3
5. KÜRE
117
5. KÜRE
Uzayda sabit bir noktadan eşit uzaklıktaki noktaların kümesine küre
yüzeyi, bu yüzeyle sınırlanan cisme küre denir.
Bu sabit noktaya kürenin merkezi, sabit
M
uzaklığa da kürenin yarıçapı
r
denir.
M −merkezli, r−yarıçaplı küre K(M, r) ile
gösterilir.
5.1. Kürenin Belirlenmesi. Fakrlı iki noktanın bir doğru, doğrudaş
olmayan üç nokta bir çember belirttiği gibi bir düzlem içinde bulunmayan
dört nokta da bir küre yüzeyi belirtir. Aynı düzlemde olmayan A, B, C ve
D noktaları verildiğinde bu noktaların belirtiği küre yüzeyi aşağıdaki şekilde
bulunur.
D
M
r
A
A, B ve C noktalarının belirttiği çemberin merkez noktasında düzleme
dik olan doğru (n-normal) üzerindeki her noktanın A, B ve C noktalarına
olan uzaklığı eşittir.
[AD]−sının orta dikmesinin n doğrusu ile kesim noktasını M dersek
|M A| = |M D| ve M ∈ n olduğundan |M B| = |M C| dir, yani M noktası,
verilen dört noktaya da eşit uzaklıkta olup M noktasını merkez r = |M D|
118
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
uzaklığını yarıçap kabul eden küre yüzeyi verilen dört noktanın belirttiği
küre yüzeyidir.
C
A
M
Ayrıca, uzayda bir doğru parçasını dik açı
B
altında gören noktaların geometrik yeri,
bu doğru parçasını çap kabul eden bir küre
yüzeyidir.
5.2. Kürenin Alan ve Hacminin Hesaplanması. Bir küre yüzeyinin
alanı ve kürenin hacmini hesaplamadan önce aşağıdaki önermelerin doğruluğunun gösterilmesi gerekir.
Teorem 7.8. Bir doğru parçasının bir eksen etrafında döndürülmesiyle
oluşan yüzeyin alanı, bu doğru parçasının orta noktasının bu dönme esnasında çizdiği çemberin çevresi ile doğru parçasının uzunluğunun çarpımına
eşittir.
İspat: Verilen doğru parçası ile eksenin durumuna göre aşağıdaki ihtimaller söz konusudur,
1) [AB]//d ise elde edilen yüzey bir silindirin
yan yüzeyi olup alanı
B
B′
C
H
A
A′
Ya = 2π|CH||AB| = 2πrh
2) A ∈ d ise yüzey bir konin yan yüzeyidir, alanı
B
Ya = π|AA′ ||AB| = 2π|CH||AB|
|AA′ | = 2|CH| olduğunu göstermeliyiz.
C
A
H
A′
5. KÜRE
119
A.A.A benzerlik teoremine göre
△
△
BCH ∼ BAA′ ⇒
|CH|
1
|BC|
=
= ⇒ |AA′ | = 2|CH|
′
|BA|
|AA |
2
3) [AB] doğru parçası eksene paralel değil
ve kesişimleri boş küme ise, yüzey bir
kesik konin yan yüzeyi olup, alanı
B
Ya = π(|AA′ | + |BB ′ |)|AB| = 2|CH||AB| C
A
⇒ |AA′ | + |BB ′ | = 2|CH|
B′
H′
D
H
E
A′
olduğunu gösterelim,
△
△
BCH ′ ∼ BAD ⇒
|CH ′ |
1
|BC|
=
= ⇒ |AD| = 2|CH ′ |
|BA|
|AD|
2
|AA′ | + |BB ′ | = |AD| + |DA′ | + |DA′ | = 2|CH ′ | + 2|H ′ H|
= 2(|CH ′ | + |H ′ H|) = 2|CH|
Sonuç 7.10. [EC] ⊥ [AB] olmak üzere |CH||AB| = |CE||A′ B ′ | dür.
B
B′
C
A
H
D
E
A′
ˆ ∼
ˆ
İspat: [AA′ ]//[CH] ⇒ A′ AC
= HCB
ˆ
ˆ ∼
ˆ
m(ECH)
= 90 − m(HCB) = m(B̂) ⇒ ECH
= ABD
A.A. benzerlik sonucuna göre
120
7.
△
△
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
CHE ∼ BDA ⇒
|HE|
|CE|
|CH|
|CH|
=
=
= ′ ′
|BD|
|DA|
|BA|
|B A |
⇒ |CH||AB| = |CE||A′ B ′ |
Teorem 7.9. r-yarıçaplı kürenin alanı S = 4.π.r2 br2 dir.
İspat: M merkezli r-yarıçaplı bir yarım çemberi ele alalım. Bu çember
yayının çap etrafında döndürülmesiyle r-yarıçaplı küre yüzeyi oluşur. Bu
küre yüzeyinin alanını hesaplayabilmek için bu yarım çember içerisine nkenarlı bir düzgün çokgen çizelim.
C
B
D
h
B′
A
M = C′
D′
E
Şekil 16. Kürenin alanı
Bu yarım çokgenin AE- doğrusu etrafında döndürülmesiyle oluşan yüzeyin
alanı Teorem 7.8 ve Sonuç 7.10 dan
Y = 2.π.h(|AB ′ | + |B ′ M | + |M D′ | + |D′ E|)
= 2.π.h.|AE| = 2.π.h.2r = 4.π.h.r br2
n −→ ∞ için h −→ r ve Y −→ S = 4.π.r2 br2 elde edilir.
4
Teorem 7.10. r-yarıçaplı kürenin hacmi, V = .π.r3 br3 dür.
3
İspat: M -merkezli ve r-yarıçaplı bir yarım küre verilmiş olsun. Taban
yarıçapı ve yüksekliği r olan bir dik dairesel silindiri göz önene alalım.
Bu silindir ile tabanı silindirin tavanını ve tepe noktası silindirin taban
merkezi olan koninin farkından oluşan cismi ele alalım. Bu cisimle yarım
küre tabanlarından aynı uzaklıkta bir düzlemle kesildiğinde elde edilen halka
ve dairenin alanları eşittir.
5. KÜRE
121
a
d
d
Şekil 17. Kürenin hacmi
Cavalier prensibine göre bu iki cismin hacimleri de eşit olmalıdır.
Cismin hacmi = silindirin hacmi - koninin hacmi, yani
(5.13)
2
1
(yarım kürenin hacmi)
V = π.r2 .r − π.r2 .r = π.r3 br3
3
3
4
2
⇒ V (K) = 2. π.r3 = π.r3 br3
3
3
Örnek 5.1. Yarıçapı r ve yüksekliği h olan bir dönel silindirle bu silindire
içten teğet olan bir küre veriliyor. Küre ile silindirin alanları ve hacmleri
arasındaki ilişki nedir?
Çözüm: Verilenlere göre h = 2r olup, taban yarıçapı r ve yüksekliği h
olan bir dönel silindirin alanı
Ss = 2πr2 + 2πr.2r = 6πr2 br2
r−yarıçaplı kürenin alanı ise,
Sk = 4.πr2 br2
dir. Buna göre
Sk
4.πr2 br2
2
2
=
= ⇒ Sk = Ss
2
2
Ss
6πr br
3
3
122
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
M
r
h = 2r
Benzer düşünceyle hacimler için de
2
Vk = Vs
3
olduğu gösterilebilir.
5.3. Küreden Elde Edilen Kavramlar. Bir K(M, r)−küresi ve bir
E-düzlemi verildiğinde, M noktasının E düzlemine olan uzaklığı |M H| = d
olmak üzere;
1) d > r ise, K ∩ E = ⊘ dir,
2) d = r ise K ∩ E = {T } olup düzlem küreye teğettir,
3) d < r ise K ∩ E = C(H, r′ ), yani arakesit bir dairedir.
Tanım 7.11. Bir K(M, r) küresi verildiğinde, bu kürenin bir düzlemle
arakesiti bir dairedir. Düzlem, kürenin merkezinden geçerse, yani d = 0 ise
elde edilen daireye, kürenin büyük dairesi denir.
Kürenin merkezinden çok sayıda düzlem geçtiğinden, bir kürenin sonsuz
sayıda büyük dairesi vardır. Bir büyük dairenin merkezi, kürenin merkezi ve
yarıçapı kürenin yarıçapı olduğundan alanı S = πr2 br2 dir.
Sonuç 7.11. r-yarıçaplı bir kürenin alanı, bir büyük dairesinin alanının
dört katına eşittir.
5. KÜRE
123
Sonuç 7.12. Bir küre yüzeyinin
herhangi bir düzlemle ara kesiti,
r′
M
merkezi H ve yarıçapı
p
r ′ = r 2 − d2
olan bir çemberdir
5.3.1. Küre Kuşağı ve Küre Kapağı.
Tanım 7.12. Bir küre yüzeği paralel iki düzlemle kesildiğinde, düzlemler arasında kalan kısmına küre kuşağı, düzlemler arasındaki uzaklığa da bu
kuşağın yüksekliği denir.
Bir küre kuşağı ve 0 < b < a ≤ r olmak üzere, a ve b-yarıçaplı dairesel
bölgelerle sınırlanan cisme yüksekliği h olan küre plakası denir.
b = 0 ve a < r olması durumunda, yani bir küre yüzeyinin bir düzlemle
kesilerek elde edilen iki parçadan küçük olanına küre kapağı, küre kapağı ile
kesit düzleminin arasında kalan cisme küre parçası denir.
b
r′
B
C
A
a
h
d
M
M
A
H
h
Şekil 18. Küre kuşağı ve Küre parçası
B
Teorem 7.11. Bir K(M, r) küresinden kesilen, h−yüksekliğindeki
a) küre kuşağının alanı
Sku = 2πrh br2
124
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
b) küre kuşağının hacmi
1
Vku = πh(3a2 + 3b2 + h2 ) br3
6
c) küre kapağının alanı
Ska = 2πrh br2
d) küre parçasının alanı
Sp = πh(4r − h) br2
e) küre parçasının hacmi
dür.
1
Vp = πh2 (3r − h) br3
3
İspat:
a) Teorem 7.8 den şekil 18 de [AB]−doğru parçasınının oluşturduğu
yüzeyin alanı
S = 2π|CH||AB| = 2π|CM |h br2
d yayı alınırsa elde edilen yüzey küre kuşağı ve
dir. Burada [AB] yerine AB
|CM | → r olacağından küre kuşağının alanı Sku = 2πrh br2 olur.
b) Küre kuşağının hacmi, aynı yarıçap uzunluğuna sahip ve aynı yüksek-
likte kesilen bir silindir tabakasından, taban ve tavan yarıçap uzunlukları d
ve (d+h) olan kesik koninin çıkarılmasıyla elde edilen cismin hacmine eşittir.
b
a
h
h
d
M
d
M
Şekil 19. Küre kuşağının hacmi
Buna göre küre kuşağının hacmi, 4.11 den,
(5.14)
1
V (Kku ) = πr2 h − πh[d2 + d(d + h) + (d + h)2 ]
3
5. KÜRE
125
diğer tarftan
1
dh = (a2 − b2 − h2 )
2
değerleri 5.14 de yerine yazılırsa
d 2 = r 2 − a2 ,
ve
(d + h)2 = r2 − b2
1
Vku = πh(3a2 + 3b2 + h2 ) br3
6
(5.15)
elde edilir.
c) Eğer b = 0 ise küre kapağı elde edilir.
d) Küre parçasının alanı ise kapğın alanına taban dairesinin alanı ilave
edilerek bulunur, yani b = 0 için a2 = r2 − (r − h)2 olduğundan
(5.16)
Sp = πa2 + 2πr.h = πh(2r − h) + 2πr.h = πh(4r − h) br 2
elde edilir.
e) 5.15 de b = 0 ve a2 = r2 − (r − h)2 alınırsa, küre parçasının hacmi,
1
Vp = πh2 (3r − h) br3
3
(5.17)
olarak elde edilir.
Örnek 5.2. Yarıçapı r = 6 cm olan bir küre yüzeyi paralel iki düzlemle
alanları bir birine eşit üç kısma ayrılmıştır. Elde edilen küre parçaları ile
küre kuşağının hacimlerini bulunuz.
Çözüm: Yarıçapı r = 6 cm olan küre yüzeyinin alanı
S = 4πr2 = 144π cm2
ve hacmi
4
V = πr3 = 288 cm3
3
dür. Bu yüzey alanları eşit üç parçaya bölündüğünde iki kapak ve bir kuşak
elde edilir.
Bir kapağın alanı,
Ska = 2πr.h = 12πh =
144
π = 48π cm2 ⇒ h = 4 cm
3
126
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
h=4
b
h′ = 2
a=r=6
Şekil 20. Küre kuşağı ve küre parçasının hacmi
bulunur. O halde bir kapağın hacmi,
16 × 14
224
1
π=
π cm3 olur.
Vka = πh2 (3r − h) =
3
3
3
Kuşağın hacmi ise h′ = r − h = 2 cm, a = r = 6 cm ve b2 = 32
olmak üzere
416
1
π cm3
Vku = 2 × πh′ (3a2 + 3b2 + h2 ) =
6
3
elde edilir. Gerçekten
2 × Vka + Vku = 2 ×
224
416
π+
π = 288 cm3 = V dir.
3
3
5.3.2. Küre Dilimi.
Tanım 7.13. Kürenin, bir [N S]−çapından geçen iki yarım düzlem arasında
kalan kısmına küre dilimi denir.
Küre dilimini oluşturan yarım düzlemler arasındaki açı bir merkez açıdır.
ˆ B−merkez açısının gördüğü küre dilimi
Şekilde M −merkezli kürede, AM
görülmektedir.
Teorem 7.12. Bir kürenin, ölçüsü α olan merkez açısının gördüğü küre
diliminin
5. KÜRE
127
N
M
S
Şekil 21. Küre dilimi
a) alanı,
Sd = πr2
b) hacmi,
α
α
+ πr2 = πr2 (1 + ) br2
90
90
Vd = πr3
α
br3 dir.
270
5.3.3. Küresel Koni.
Tanım 7.14. Bir K(M, r)−küresinden, bir [AX−ışınının [AB] çapı veya
bir yarıçapın başka bir yarıçap etrafında döndürülmesiyle kesilen kısmına
küresel koni denir.
B
h
X
H
M
M
A
Şekil 22. Küresel koni
128
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
Bir küresel koni, yarıçapı a ve yüksekliği h olan bir küre parçası ile
yüksekliği (2r − h) veya (r − h) olan bir dik dairesel koninin birleşimidir.
Buna göre,
a = |HX| ve a2 = h(2r − h),
ˆ
α = m(BAX)
⇒ sin α =
a
a
⇒ |AX| =
olmak üzere,
|AX|
sin α
1) eğer koni, bir [AX−ışınının [AB] çapı etrafında döndürülmesiyle oluşmuş ise,
a) alanı
(5.18)
Skk = πh(2r +
2r − h
) br2
sin α
b) hacmi ise
(5.19)
1
Vkk = πrh(4r − h) br3
3
2) eğer koni, bir yarıçapın başka bir yarıçap etrafında döndürülmesiyle
oluşmuş ise,
a) alanı
(5.20)
Skk = πr(2h + a) br2
b) hacmi
(5.21)
2
Vk = πr2 h br3
3
dür.
Örnek 5.3. Çapı 6 cm olan kürenin bir [AB]−çapı ile θ = 30o lik açı yapan bir [AX ışını [AB]−çapı etrafında döndürülerek kesilen küresel koninin
alanını ve hacmini bulunuz.
çözüm:
1
ˆ
m(BAX)
= α = 30o ⇒ sin α =
2
5. KÜRE
X
d
129
B
h
X
H
X′
M
r
A
A
Şekil 23. Küresel koni
△
|AX| = |AX ′ | ⇒ XAX ′
bir eşkenar üçgendir. M noktası bu üçgenin ağılık merkezi olup
3
1
3
9
|HM |
= ⇒ |HM | = ⇒ |HA| = ⇒ |HB| = h =
|M A|
2
2
2
2
bulunur. Bu değerler 5.18 ve 5.19 da yerine yazılırsa elde edilen küresel
koninin alanı
Skk =
45
π cm2
2
hacmi ise, Vkk =
63
π cm3 olarak bulunur.
4
130
7.
KATI CİSİMLERİN ALAN VE HACİM HESAPLARI
NOTASYONLAR
AB,
AB−doğrusu
[AB],
AB−doğru parçası
|AB|,
AB−doğru parçasının uzunluğu
[AB,
AB−ışını
d
AB,
AB−yayı
d
m(AB),
AB−yayının ölçüsü
d
|AB|,
AB−yayının uzunluğu
A−açısının ölçüsü
m(Â),
△
ABC üçgeni
ABC,
G,
ağırlık merkezi
H,
yükseklik ayağı
ha ,
a- kenarına ait yükseklik
∼
=,
eşlik işareti
∼,
benzerlik işareti
//,
paralellik işareti
⊥,
diklik üşareti
karşılıklı bire bir eşleme
←→
M −merkezli, r−yarıçaplı çember
C(M, r),
K(M, r),
M −merkezli, r−yarıçaplı küre
merkez açısı α olan daire dilimi
Dd (α),
n−kenarlı çokgen
(Pn )(T, Pn )-
tepe noktası T olan piramit
Sp -
küre parçasının alanı
Vp -
küre parçasının hacmi
Sd -
küre diliminin alanı
Vd -
küre diliminin hacmi
Skk -
küresel koninin alanı
Vkk -
küresel koninin hacmi
Index
Üçgen Eşitsizliği, 25
dış ortak teğet, 75
önerme, 1
dış teğet çember, 83
üçgen, 19
Dışbükey Çokgen, 58
İç Açı, 71
dayanak eğrisi, 111
İçbükey Çokgen , 58
değme noktası, 63
ışın, 3
deltoid, 57
Çevre Açı, 69
dik dairesel koni, 114
çap, 64
dik dairesel silindir, 112
çember, 63
dik silindir, 112
çevrel çember, 84
dikdörtgen, 55
çokgen, 58
doğru, 2
doğru parçası, 3
merkez açı, 68
eğik koni, 114
açı, 9
eğik silindir, 112
açıortayı, 10
elips, 88
aksiyom, 1
enine kesit, 102
aykırı doğrular, 7
geometrik yer, 86
Cavalier Prensibi, 107
hüküm, 1
dönel konin, 114
dönel silindir, 113
iç ortak teğet, 75
dörtgen , 49
iç teğet çember, 83
düzgün çokgen, 59
ikizkenar yamuk, 53
düzgün dört yüzlü, 110
düzgün piramit, 106
köşegen, 49
dış açı, 72
küre dilimi, 126
131
132
INDEX
küre yüzeyi, 117
yamuk, 51
kürenin büyük dairesi, 122
yan ayrıtlar, 102
küresel koni , 127
yan yüz, 102
kare, 56
yanal yüzeyi, 112
Kenarortay, 21
yay , 68
kesen, 63
kesik koni, 115
kiriş, 64
kirişler dörtgeni, 85
koni, 113
koni yüzeyi, 113
kuvvet, 77
kuvvet ekseni, 79
kuvvet merkezi, 81
Menelaus Teoremi, 41
orta nokta, 5
paralel doğrular, 7
paralel kenar, 54
piramit, 105
Pisagor Teoremi, 46
Pisagor teoremi, 77
prizma, 101
Seva Teoremi, 43
Tales Teoremi, 39
tanımsız kavram, 1
teğet, 63
Teğet-Kiriş Açı, 71
teğetler dörtgeni, 85
Temel İlkesi, 5
tepe noktası, 105
Yükseklik, 22