5. Uluslararası İleri Teknolojiler Sempozyumu (IATS’09), 13-15 Mayıs 2009, Karabük, Türkiye
ÜÇ FAZ TRANSFORMATÖRLERİN HARMONİK MODELLEMESİ
HARMONIC MODELLING OF THREE PHASE TRANSFORMERS
Mehmet Zile
Mersin Üniversitesi, Mersin, Türkiye, E-posta: [email protected]
Özet
Güç sistemlerinin harmonik analizinde bütün elemanlar
harmonik frekans bölgesinde gösterilmelidir. Bu bildiride,
doğrusal olmayan elemanların, katlanma eşdeğer zaman
bölgesi
çarpımları
kullanılarak
harmonik
frekans
bölgesinde direk olarak nasıl gösterileceği anlatılmıştır.
Yöntem güç trafolarına uygulanarak incelenmiştir.
Doğrusal olmayan elemanların direk harmonik frekans
bölgesinde gösterilmesi için genel bir yöntem tanımlanmış
ve transformatör modelleme metoduna uygulanmıştır.
Anahtar kelimeler: Üç Faz Transformatör, Harmonikler
Abstract
Harmonic phenomena in three phase transformers are
quite important. It is because under certain conditions, the
exciting current harmonics may cause inadvertent
operation of the protective equipment and may also cause
interface with communication circuits. The study is to
discuss the harmonics in three phase transformers. For the
harmonic analysis of power systems, it is essential to have
all compenents represented in the harmonic frequency
domain. This study shows how nonlinear elements can be
directly represented in the harmonic domain by using a
convolution equivalent to time domain multiplications. The
procedure is then applieed to power transformers.
Keywords: Three-Phase Transformer, Harmonics
1. Giriş
Harmonikler çeşitli sebeplerle ortaya çıkar. Bunların
başında doğrusal olmayan manyetik ve elektrik devreleri
gelir. Bunlar jeneratör, transformatör ve bobin gibi demir
nüve bulunan manyetik devrelerdir. Doğrusal olmayan
devre, jeneratörün manyetik devresi ise jenaratörün ürettiği
gerilimin sinüs şeklinde olması nedeni ile harmonikli olur
[1]. Eğer doğrusal olmayan devre transformatöre ait ise,
bunun sekonder tarafına bağlanan kullanıcı gerilimi de
harmonikli olur. Kullanıcının manyetik ya da elektrik
devresi doğrusal, fakat bu kullanıcıyı besleyen gerilim
sinüs değil ise, kullanıcının çektiği akım da harmonikli olur.
Harmonik, ya kaynak tarafındaki harmonikli gerilim
etkisinden, ya da elemanın doğrusal olmayan bir devreye
sahip olmasından dolayı meydana gelir [1,2]. Akım ve
gerilim harmonikleri paralel ve seri rezonans oluşumu
sebebiyle harmoniklerin artmasına, elektrik üretim, iletim
ve tüketiminde verimin azalmasına, elektrik tesislerinde
yalıtımı zayıflattığı için tesis elemanlarının ömürlerinin
azalmasına, elektrik elemanlarında arızalar meydana
gelmesine sebep olur [3]. Güç faktörünü düzeltmek amacı
ile yerleştirilen kapasiteler, seri veya paralel rezonans
© IATS’09, Karabük Üniversitesi, Karabük, Türkiye
olayları dolayısıyla yüksek akımlara maruz kalarak zarar
görebilir.
Harmonik akımları sebebiyle, makinalar ve tranformatörler
ısınır. Ayrıca generatörlerin amortisman sargıları, bir veya
iki fazlı kısa devrelerde meydana gelen harmonikleri
azaltacak ve ortadan kaldıracak şekilde etki ederken
kendileri de çok ısınır ve jeneratörlerde ilave kayıplar
meydana gelmesine yol açar. Harmonik akımları çeşitli
devre empedansları üzerinde ilave gerilim düşümlerine
neden olur. Harmonik akımlarının frekansları, normal
şebeke frekansı 50 Hz' in katlarına eşit olduğundan, bu
akımlar karşısında generatör, transformatör ve hat
reaktansları üzerinde meydana gelen gerilim düşümleri de
harmonik frekansları ile orantılı olarak artar ve sonuç
olarak gerilimin dalga şekli bozulur. Sinüs şeklindeki
gerilim eğrisine eklenen gerilim harmoniklerinin meydana
getirdiği iğne ucu şeklinde sivri çok kısa süreli ani gerilim
yükselmeleri, mesela gerilim rezonansı gibi hallerde,
makina ve transformatör sargılarının izolasyonu ve
kondansatörlerin di-elektrik maddesi için büyük bir tehlike
teşkil eder ve hatta izolasyonda delinmeye yol açabilirler
[2,3]. Transformatörlerde harmonik gerilimleri histerizis ve
girdap akımlarını artırarak kayıpları büyütür ve yalıtımı
zorlar. Harmonik akımları bakır kayıplarını da artırır. Bu
durum, özellikle çevirici transformatörlerde önem kazanır.
Zira, harmonikleri süzmek için kullanılan filtreler alternatif
akım tarafına bağlanır, dolayısıyla harmonik üreteçleri
olarak kabul edilen doğrultucu devrelerin ürettiği
harmonikler,
filtreye
girmeden
önce
çevirici
transformatörün
üzerinden
akar.
Bu
sebeple,
transformatörün gücü artırılmalıdır. Bu ise, transformatörün
maliyetini artırır. Ayrıca bu çevirici transformatör tankı
üzerinde ısınmış noktalar meydana getirir. [4,5]
Daha önce konu ile ilgili, 1996’da N. Elleuch, relüktans
kullanarak üç faz transformatörlerin modellemesi üzerine
ve 1997’de X. Chen, endüktans matrisinin tersini direk
kullanarak üç faz çok bacaklı transformatör modeli üzerine
yaptığı çalışmalar bulunmaktadır.
2. Harmonik Katlanma (Konvolisyon)
Doğrusal
olmayan
elemanların
direk
harmonik
modellemesi, zaman bölgesi çarpımının frekans bölgeli
eşdeğeri olan ve katlanma adı verilen bu temele
dayandırılmıştır. Çarpımların zaman bölgesinde olduğu
frekans bölgesinde olmadığı görülmüştür.
x ve y iki periyodik zaman bölgesi değişkeni, x ve y ise
karşılık gelen harmonik bölgeli vektörler olsun. Böylece;
∞
x =
∑
h = −∞
xhe
jhwt
(1)
Zile, M.
∞
y=
∑y e
(2)
jkwt
k
k = −∞
ve
x = [...xh ...] = [...x− 2 , x−1 , x0 , x1 , x2 ,....]
T
T
(3)
3. Transformatör Modellemesi
y = [... y k ...] = [... y −2 , y −1 , y 0 , y1 , y 2 ...]
T
eşitlikleri ile doğrusal hale getirilir. Burada, α demir
nüvenin relüktans artımını ifade eder ve hava relüktansıyla
karşılaştığında daha küçük olduğu görülmüştür. Eşitlik 12
deki bütün katlanma işlemleri, harmonik frekans
bölgesindedir.
T
.
..
(4)
ifade çarpıldığında,
∞
∑z e
T
T
z = xy = [...z 1 ...] = [...z − 2 , z − 1 , z 0 , z 1 , z 2 ...]
jlwt
z = xy =
l
(5)
l = −∞
(6)
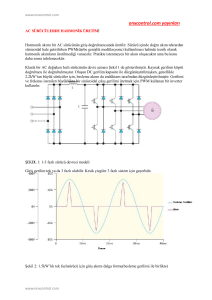
Şekil 1. ∆/Υ kapasitif yüklü transformatör
Eğer eşitlik 1 ile 2’ yi eşitlik 5’ de yerine koyup ve
katsayılarıyla karşılaştırdığımızda, aşağıdaki ifade bulunur.
Bütün h+k=1
z1 = ∑ xk . y k
(7)
veya
∞
z1 =
(8)
∑x y
h l−h
h = −∞
Böylece açık olarak çarpım z=x.y, z’nin bütün z1 elemanları
için eşitlik 8 katlanma değerlerini (konvolüsyonları)
gösterir. Aynı zamanda, eşitlik 1 ve eşitlik 3’ den,
.
x = [... jhwxh ...] = diag ( jhw) x
T
(9)
Şekil 2. Tek fazlı transformatör
Şekil 2’ de gösterilen tek fazlı transformatörün manyetik
yapısı incelendiğinde aşağıdaki eşitlikler elde edilir.
elde edilir. Böylece zaman bölgesindeki diferansiyel,
karşılık gelen harmonik frekans bölgeli ‘diag (jhw)’ diagonal
matrisin bir ön çarpımıdır. Sonuçta, polinom biçiminde
yazılmış zaman bölgesinde diferansiyel eşitlik, harmonik
bölgeli katlanma teoremi uygulanarak elde edilmiştir.
Doğrusal olmayan mıknatıslama karakteristikleri ele
alındığında,
∆Φ P = ∆Φ S + ∆Φ l
(15)
∆FP = α P .∆ΦP
(16)
∆FS = α S .∆Φ S
(17)
(10)
∆Fl = β .∆Φl
(18)
N P .∆ip = ∆FP + ∆Fl
(19)
F = c1 .Φ + c3 .Φ 3
manyetik akı Φ, manyetik motor kuvveti F ile gösterilirse,
harmonik frekans bölgesinde eşitlik 10,
F= c1.Φ+c3.Φ
3
(11)
N S .∆is = ∆FS + ∆Fl
(20)
∆vP = rP .∆iP + N P . p.∆Φ P
(21)
∆vS = rS .∆iS + N S . p.∆ΦS
(22)
3
olur. Φ = (ΦΦ)Φ işlemi sıralı katlanmaları ifade eder.
Böylece, F vektörü harmonik bölgesinde direk olarak
hesaplanır. Eğer sürekli hal çalışmada Φ harmonik içeriği
küçük ise, eşitlik 11 Φ 0 , F0 , We nin sinüs biçimli halini
∆F = F − F0 = α .∆Φ
(12)
dır. Bu eşitliklerde, ∆Φ l kaçak akı artımını, ∆Fl manyetik
motor kuvvetini, β kaçak yol relüktansını ifade eder.
F0 = c1Φ 0 + c3 Φ 30
(13)
β>>α
α = c1 .1 + 3.c3 .Φ 02
(14)
Eşitliklik 21 ve 22 matrisel biçimde aşağıdaki gibi yazılır.
(23)
Zile, M.
− β ∆Φ P N P .∆ip
α P + β
−β
= N .∆is
α
S + β ∆Φ S
S
(24)
Eşitlik 11 ve eşitlik 12 den,
∆Φ P =
1
(∆vP − rp ∆iP )
NP. p
(25)
∆Φ S =
1
(∆vS − rs ∆iS )
NS . p
(26)
elde edilmiştir. Eşitlik 25 ve eşitlik 26, eşitlik 24 de yerine
koyup düzenlediğimizde aşağıdaki eşitlik elde edilir.
GN norton admitans matrisini ifade eder. Boyutu bütün
primer ve sekonder harmonik elemanları içeren v ve i ye
karşılık gelir. Eğer şekil 2 de üç adet tek faz trafo üniteleri,
şekil 1 de gösterildiği gibi ifade edilirse, eşitlik 34 ile
transformatörün tam harmonik modelini elde edilir. Sistem
çıkışı için norton eşdeğeri, aşağıdaki gibi elde edilmiştir.
(34)
i ' = G ' N .v + i ' N
∆v ve ∆i hesaplanır. Tek ünite içinde geriye gidildiğinde
∆Φ p ve ∆Φ s eşitlik 25 ve eşitlik 26 dan ve diğer
değişkenlerde eşitlik 15-22 den elde edilir. İkinci bir örnek
olarak, şekil 3 deki üç bacaklı transformatör göz önüne
alındığında, primeri (a,b,c) yıldız, sekonderi (a’,b’,c’) üçgen
bağlıdır.
(27)
∆i = G N .∆v
eşitlik 27 genişletildiğinde,
(28)
i − i0 = G N .(v − v0 )
veya
(29)
i = G N .v + i N
dir. Eşitlik 29, transformatör modelinin norton eşdeğerine
karşılık gelir. Harmonik frekans bölgesindeki eşitlik 29 dan,
eşitlik 33 de verilen ifade elde edilir.
i=GN.v + iN
αp + β
N p. p
rp .(α p + β )
Np +
N p. p
GN =
−β
N p. p
(α s + β ).rs
Ns + N . p
s
(30)
−β
Ns . p
rp .(α p + β )
Np +
N p. p
αs + β
Ns . p
(α + β ).rs
Ns + s
Ns . p
Şekil 3 Yıldız-üçgen bağlı üç faz transformatör
Primer ve sekonder sargılar arasındaki kaçak akılar Φ 1a ,
Φ 1b , Φ 1c , sıfır sıralı kaçak akı ise Φ 0 ile gösterilir. Çatal
akılar Φ ab ve Φ cb dir. Akılar için süreklilik denklemleri,
.
(31)
∆Φ a = ∆Φ ab + ∆Φla
(35)
∆Φ c = ∆Φ cb + ∆Φ lc
dır. Manyetik motor kuvveti ise,
∆Fi = α .∆Φi
(i = a, b, c ) , ∆Fab = α '.∆Φ ab
,
'
∆Fcb = α .∆Φ cb
∆Fli = β .∆Φ li i = (a, b, c) , ∆F0 = β 0 .∆Φ0
∆i p
∆v p
∆i = GN . ∆v + iN
s
s
(32)
(36)
ve şekil 3 de altı manyetik yol için karşılık gelen amper
sarımları,
N P ∆ia = ∆Fa + ∆Fla
0
iN =
β .rp
(
N + α s + β ).rs
s
Ns. p
Np +
β .rs
rp .(α p + β )
N p.p
0
i p
. i
s
N S ia ' = − ∆Fla + ∆Fab + ∆F0
N P ∆ib + N S ∆ib ' = ∆F0 + ∆Fb
(33)
N P ∆ib = ∆Fb + ∆Flb
− N S ∆ib ' + N S ∆ic ' + N P ∆ic = ∆Flb + ∆Fcb + ∆Fc
N P ∆ic = ∆Fc + ∆Flc
dır. Sargı gerilimleri ise,
(37)
Zile, M.
edilmiştir. Sıfır sıralı harmonik
bulunmadığı araştırılmıştır.
∆va − ∆v0 = rP .ia + N P . p.∆Φ a
∆vb − ∆v0 = rP .ib + N P . p.∆Φb
∆vc − ∆v0 = rP .ic + N P . p.∆Φ c
∆va ' − ∆vb ' = rS ia ' + N S . p.∆Φ a
(38)
∆vb ' − ∆vb ' = rS .ib ' + N S . p.∆Φ b
∆vc ' − ∆va ' = rS .ic ' + N S . p.∆Φ c
dır. Nötür için aşağıdaki ifade elde edilmiştir.
∆ia + ∆ ib + ∆ic = 0
(39)
Yukarıda verilen 25 adet eşitlikteki değişken sayısı 31 dir.
Bunların dokuz tanesi akı, dokuz tanesi manyetik motor
kuvveti, altı tanesi akım ve yedi tanesi gerilim eşitliğidir.
Eğer bu eşitliklerden akıları, manyetik motor kuvvetlerini ve
∆v0 çıkarıldığında, on iki adet ∆v ve ∆i değişkeninde altı
tane eşitlik kalır. Bunlar eşitlik 27 biçiminde tekrar
düzenlenmiştir.
Doğrusal olmayan elemanlar, transformatörlerdeki gibi
harmonik frekans bölgesinde ve türetilebilen norton
eşdeğerlerinde doğrusal hale getirilmiştir. Norton eşdeğeri
ile bütün harmonikler tek adımda hesaplanmıştır.
Doğrusallaştırarak elde edilen norton eşdeğeri, harmonik
frekans bölgesi sistemdeki yineleyici çözümün temelini
oluşturmuştur.
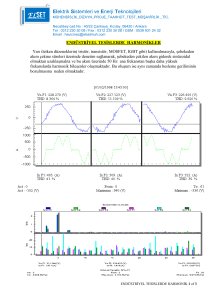
4. Deneysel Çalışma
Şekil 4 Deneysel Çalışma
Laboratuar deneyleri genel olarak iki kısımdan oluşmuştur.
Birinci kısım histerisiz eğrisini ve uyarma akımının
sinüzoidal olmayan dalga şeklini analiz ederek, tek faz
transformatör nüvesinin doğrusal olmadığı ispatlanmıştır.
İkinci kısım ise, transformatör akımı ve karşılıklı akı dalga
şekilleri üzerinde farklı üç faz transformatör bağlantılarının
etkileri incelenmiştir. Birinci kısımda, sinüzoidal dalga
şekillerinin fourier serileri ile tanımlanmış, harmonik
bileşenler
sınıflandırılmış
ve
farklı
transformatör
bağlantılarında elde edilen faz gerilim ve akım dalga
şekilleri elde edilmiştir. Deneysel olan ikinci kısımda ise,
akım ve gerilim dalga şekilleri ve harmonik içerikleri
gösterilmiştir. Osilaskop kullanılarak farklı akımlar ve
gerilim dalga şekilleri kaydedilmiştir. Harmonik analizör
kullanarak her bir dalga şeklinin harmonik içeriği analiz
bileşenlerin
bulunup
Deney düzeneği, 3 faz 4 iletkenli besleme, 120 V/60 V - 60
VA. lik üç faz kabuk tipi transformatör, akım probları,
kameralı osilaskop ekipmanı ve verileri işlemek depolamak
ve dalga şekillerini yeniden oluşturmak için bilgisayarlı bir
harmonik analizör elemanlarından oluşmuştur. Gerilim ve
uyarma akımlarının harmonik genliğini belirlemek için,
harmonik analizör ve bilgisayar kullanılmıştır. Harmonik
modelleme ile elde edilen değerler ile ölçülen değerlerin
aynı olduğu görülmüştür.
5. Sonuç
Akım ve gerilim harmoniklerin etkileri, paralel ve seri
rezonans dolayısıyla harmonik seviyelerinin yükselmesi,
elektrik üretim, iletim ve tüketiminde verimin azalması,
elektrik tesislerinde yalıtımı zayıflattığı için tesis
elemanlarının ömürlerinin azalması, tesislerde arızalar
meydana getirmesidir. Elektrik tesislerinde güç faktörünü
düzeltmek amacı ile yerleştirilen kapasiteler, seri yada
paralel rezonans olayları sebebiyle yüksek akımlara maruz
kalarak zarar görür. Paralel rezonans durumunda,
rezonans frekansında harmonik üreten kaynak yüksek
değerde bir empedansla karşılaşılır. Paralel rezonans
değişik şekillerde meydana gelir. İlk akla gelen şekli, bir
kapasitenin harmonik
üreten kaynakla aynı baraya
bağlanması ile ortaya çıkar. Bu, harmonik kaynağı ile
kapasite arasında bir paralel rezonans meydana getirir.
Seri rezonans etkisi, yüke paralel olarak bağlanan
kapasitenin
empedansı yüksek frekanslarda çok
düşeceğinden dolayı, omik yük göz önüne alınmayabilir.
Transformatörün selfi ile güç faktörünü düzeltmek amacı
ile yerleştirilen kapasite arasında seri rezonans meydana
gelebilir. Seri rezonans devresinde yüksek değerde
kapasite akımları, fakat düşük harmonik gerilimleri
gözlenir.
Güç trasformatörlerinde ise üçlü harmonikler, üçgen sargı
içinde dolaşır. Eğer transformatör tasarımında bu etki
düşünülmemiş ise, bu etki önemsenmeli ve tedbir
alınmalıdır. Eğer transformatör asimetrik bir yükle
yüklenirse, yük akımının doğru akım bileşeni içermesi
durumunda transformatörün manyetik devresi doymaya
gidecek ve uyarma akımının tüm harmonik bileşen
seviyeleri artacaktır. Şebeke ve kapasite arasında
meydana gelen seri ve paralel rezonans yüzünden oluşan
aşırı gerilim ve yüksek akım harmonikleri kapasiteleri ısıtır
ve hatta tahrip eder.
Güç sistemlerinin harmonik analizinde, bütün elemanlar
harmonik frekans bölgesinde gösterilmelidir. Bu çalışmada,
doğrusal olmayan elemanlar katlanma (konvolüsyon)
eşdeğer zaman bölge çarpımları kullanılarak, harmonik
bölgesinde direk olarak nasıl gösterileceği anlatılmıştır.
Sistemde birçok harmonik üreten elemanlardan dolayı, güç
sistem harmonik analizleri önemli hale gelmiştir. Bütün
sistem elemanlarının harmonik frekans bölgesinde
modelleri olmalıdır. Doğrusal olmayan elemanların direk
harmonik bölgesinde göstermek için, genel bir yöntem
tanımlanmış ve transformatör modelleme metoduna
uygulanmıştır.
Zile, M.
Kaynaklar
[1] Dommel, H.W., Yan, A., ve Wei, S., Harmonics from
Transformer Saturation, IEEE Trans on Power
Systems, vol. PWRD-1, 209-214, 1986.
[2] Wilson, Xu, Multiphase Harmonic Load Flow Program
(MHLF) Reference Manual, 1991.
[3] Keyhani, A., Nonlinear Modelling of Magnetic
Saturation, Electr. Power Syst. Res.,15-24., 1988.
[4] Ell, L.K., Councill, M.E., Distribution Transformer
Excitation Harmonics Power Systems Research, Vol.
17, 13-19, 1989.
[5] Lin, C. E., Cheng, C. L., Huang, C. L. ve Yeh, J. C., A
Simple Model for Transformer Inrush Electric
Calculation and Harmonic Analysis, Electric Power
System Research, Vol. 24, No. 2, 153-163., 1992.
[6] Anderson, O., Large Transformers for Power
Electronic Loads, IEEE transactions on power
delivery, Vol 12, No.4, 1532-1537, 1997.
[7] Juan W. D., Gustavo V., Luis A. M., A Series Active
Power filter Based on a Sinusoidal Current-Controlled
Voltage-Source Inverter, IEEE Transactions On
Industrial Electronics, Vol:44, No:5, 612-620, 1997.
[8] Member, Chi-Jui Wu, Developing a Harmonics
Education Facility in a Power system Simulator for
Power Engineering Education, IEEE Transactions On
Power Systems, Vol:12, No:1, 22-29, 1997.
[9] Mielczarski, Wladyslaw, Harmonic Current Reduction
in Three-Phase Bridge-Rectifier Circuits Using
Controlled Current İnjection, IEEE Transactions on
İndustrial electronics, Vol:44, No:5, 604-611, 1999.
[10] Stensland, T., Modeling of Magnetizing and Core-Loss
Currents in Single Phase Transformers with Voltage
Harmonics for use in Power Flow.”, IEEE Transactions
On Power Delivery, Vol:12, No:2, 768-774, 1999.