14 Şubat 2011 Pazartesi günü uygulamada çözdüğümüz 2

14 Şubat 2011 Pazartesi günü uygulamada çözdüğümüz 2. Soruyu, aynı sıra ile bu defa MATLAB
kullanarak çözelim.
MATLAB programı sembolik çözümler yapabilmekle birlikte, problemleri numerik olarak çözmeye
yarar. Lisansı ücretli olan fakat İTÜ içinden erişebileceğiniz bu programa benzeyen ücretsiz
programlar da bulunmaktadır. (Octave, Numpy, Scipy, Scilab gibi) Bunların kullanımı da MATLAB’a
benzemektedir.
MATLAB programını açtığınızda karşınızda kutlarınızı çağırabileceğiniz bir “command window”
göreceksiniz. Biz komutlarımızı bir dosyaya saklamak istediğimizden, bir editör yardımıyla kodumuzu
yazıp, daha sonra çalıştıracağız. Herhangi bir editör kullanabilirsiniz, ancak renklendirmeleri size
yardımcı olacağından ben MATLAB editörünü tavsiye ederim.
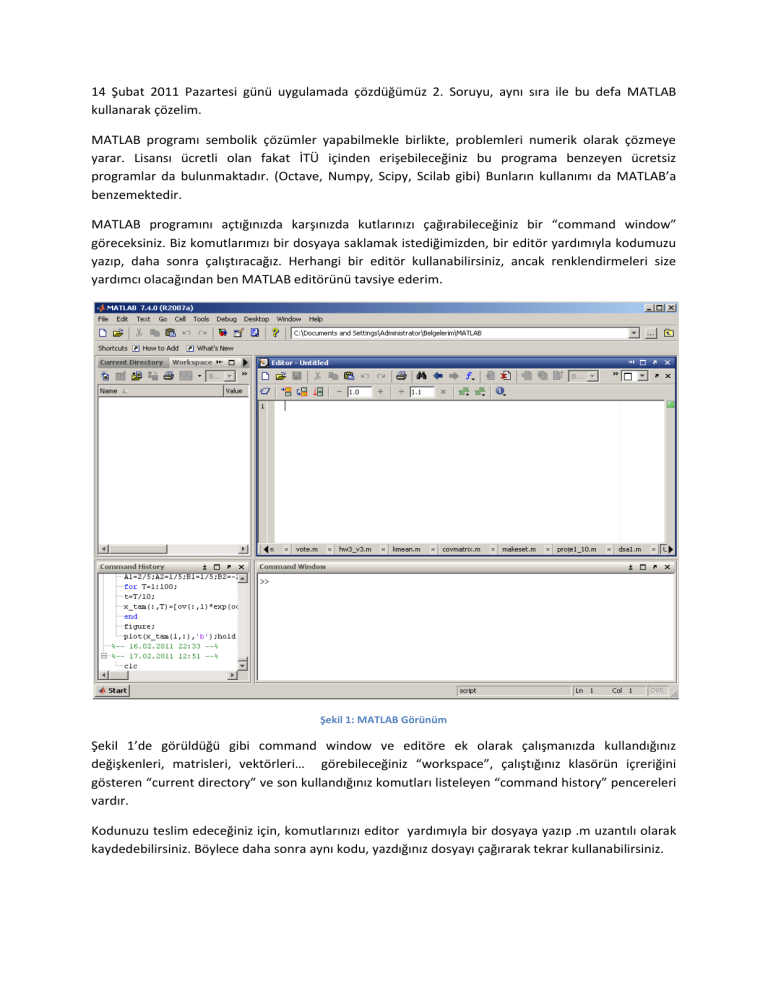
Şekil 1: MATLAB Görünüm
Şekil 1’de görüldüğü gibi command window ve editöre ek olarak çalışmanızda kullandığınız
değişkenleri, matrisleri, vektörleri… görebileceğiniz “workspace”, çalıştığınız klasörün içreriğini
gösteren “current directory” ve son kullandığınız komutları listeleyen “command history” pencereleri
vardır.
Kodunuzu teslim edeceğiniz için, komutlarınızı editor yardımıyla bir dosyaya yazıp .m uzantılı olarak
kaydedebilirsiniz. Böylece daha sonra aynı kodu, yazdığınız dosyayı çağırarak tekrar kullanabilirsiniz.
İlk önce soruda verilen matrisleri tanımlayalım.
1
1
A
1
1
Şeklinde verilen A matrisini
A = [-1 1;-1 -1];
İle yazabiliriz. Bir matris, [] ile tanımlanır. Matrisin sütunlarını ayırmak için sayılar arasında boşluk
bırakmak yeterlidir. Matrisin satırları ise ; ile ayrılır. Satır sonuna koyulan ; işareti ise command
windowda sonuçların yazdırılmamasını sağlar. Kısaca ikiye ikilik bir matris
Matris = [a11 a12; a21 a22];
Şeklinde yazılabilir. Benzer şekilde B matrisi de
B=[1 0;0 1];
olarak tanımlanabilir. Henüz yazdığınız koddan tam olarak emin olamadığınız için, kodunuzu satır satır
çalıştırmayı deneyeceksiniz. Bunun için çalıştıracağınız komutu/komutları seçili hale getirip, sağ tık ile
“Evaluate Selection” (kısayol:F9) diyebilirsiniz. A ve B matrislerini tanımladığınız satırları
çalıştırdığınızda “workspace”’te bu matrisleri göreceksiniz.
Şimdi devrenin kararlı olup olmadığını görmek için A matrisinin özdeğer ve özvektörlerini
hesaplayalım:
[ov
od]= eig(A)
eig(A) komutu A matrisinin özdeğer ve özvektörlerini hesaplamak için kullanılır. Herhangi bir işlem
için bir MATLAB komutu olup olmadığını MATLAB yardımı kullanarak bulabilirsiniz. Örneğin “Help”
penceresini açıp “eigenvalue” kelimesini aradığınızda, bu komutu bulacaksınız. Bu komutun ne iş
yaptığını ve nasıl kullanıldığını kısaca öğrenmek isterseniz command window’a “help eig” yazın.
Yukarıdaki komutu seçip çalıştırdığımızda, komutun sonuna ; koymadığımız için command window’da
aşağıdakileri göreceğiz:
ov =
0.7071
0.7071
0 + 0.7071i
0 - 0.7071i
od =
-1.0000 + 1.0000i
0
0
-1.0000 - 1.0000i
Özdeğerler od matrisinin diagonalında verilmiş. Birinci özvektör, ov matrisinin birinci sütunu, ikinci
özvektör ise ov sütununun ikinci sütunu. (Özvektörler bizim derste hesapladıklarımızla aynı değil, ama
farklı özvektör çiftleri bulabileceğinizi biliyordunuz.)
Birinci özdeğeri od1 değişkenine atayalım:
od1=od(1,1);
Benzer şekilde od vektörünün 2,2 elemanı olan ikinci özdeğeri de
od2=od(2,2);
olarak yazabiliriz. Değişken sayısını arttırmak bize bir şey kazandırmayacağından, bu iki komutu
çalıştırmaktansa, birinci özvektörü kullanmak istediğimiz yerde od(1,1) yazabiliriz. Ancak kodun
anlaşılırlığı açısından da yeni değişken tanımlamak faydalı olabilir.
Özdeğerleri command window’da görüntüleyerek özdeğerlerin jw eksenine göre yerini tayin edebilir,
dolayısıyla devrenin kararlı olup olmadığını anlayabiliriz.
Şimdi durum geçiş matrisini bulmak için M matrisini bulalım.
M=[ov(:,1)*exp(od(1,1)*t) ov(:,2)*exp(od(2,1)*t)];
* İşareti çarpma yapmak için kullanılır, ed ise exp(d) komutu ile hesaplanabilir. M matrisinin birinci
sütunu birinci özvektör ile eλ1.t nin çarpımı olduğuna göre, matrisin birinci sütun
ov(:,1)*exp(od(1,1)*t) ile hesaplanabilir. Gördüğünüz gibi, bir matrisin 1. sütununu ov(:,1) yazarak
seçebiliyoruz. Benzer şekilde 1. satırını da ov(1,:) şeklinde seçebilirdik. Dikkat ederseniz, biz şimdiye
kadar “t” değeri tanımlamadık. MATLAB ile şu anda numerik işlem yaptığımıza göre, t için de bir
değere ihtiyacımız var. Bu sebeple öncelikle t=0 için M(0) değerini hesaplayalım:
t=0;
M_0=[ov(:,1)*exp(od(1)*t) ov(:,2)*exp(od(2)*t)];
Bize bu matris değil, bunun tersi gerekiyor. Yardımda “inverse” ararsanız matris tersini alan komutu
kolayca bulabilirsiniz:
M_0_ters=inv(M_0);
Şimdi düşünelim, bizim her t değeri için M(t) matrisini kaydetmeye ihtiyacımız var mı? Yok, ama grafik
olarak çizdirmek istediğimiz özçözüm = Φ(t).x(0). Doğrudan Φ(t).x(0) değerlerini de kaydedebiliriz.
100 adet t değeri için özçözümü hesaplayıp bir matrise nasıl yazabiliriz? Aradığımız xoz(t) iki satırlı bir
vektör. Her bir t değeri için bulduğumuz değeri matrisin ilgili sütununa yazabiliriz. MATLAB satır ve
sütun indisleri için sadece pozitif tam sayıları kabul eder. Oysaki bizim ilgilendiğimiz t değerleri pozitif
reel sayılar. Bu sebeple ben matris işlemlerinde kullanabileceğim bir T değişkeni tanımlıyorum.
Aşağıda t’nin 100 değeri için özçözümü hesaplayan bir for döngüsü var. Her for döngüsü end komutu
ile bitmek zorunda. Döngünün tamamını çalıştırmak için de for ve end satırlarının seçili olduğuna
emin olun.
x_0=[1;1];
for T=1:100;
t=T/10;
x_oz(:,T)=[ov(:,1)*exp(od(1,1)*t) ov(:,2)*exp(od(2,2)*t)]*M_0_ters*x_0;
end
Yukarıdaki döngüye göre, matrisin
değeridir.
birinci sütunu (T=1 iken), t= 0.1 için hesaplanan özçözüm
İki adet durum değişkenimizin zaman içinde aldığı özçözüm değeri x_oz matrisinin satırlarında
verilmiş oldu böylece. Başka bir değişle, “x_oz(1,:)” x1 için özçözümü verir. İki çözümü de üst üste
çizdirelim:
figure;
plot(x_oz(1,:));hold all; plot(x_oz(2,:));
Figure komutu bir resim penceresi açar. plot(vektor) komutu bir vektörün elemanlarını sıra ile çizer.
Aynı figür üzerine başka eğriler de çizmek istiyorsak “hold on” deriz, aksi takdirde ikinci defa plot
komutunu çalıştırdığımızda ilk çizdiğimiz eğri siliniz. Önceki eğrileri kaybetmemenin bir yolu da her bir
plot komutundan önce figure komutu ile yeni bir pencere açmaktır.
Şekil 2: Özçözüm 1
Ben yukarıdaki gibi bir resim elde ettim. Çizgilerin rengiyle, şekliyle, eksen isimleri ile oynayıp,
eğrilerin ismini komutlarla da değiştirebilirsiniz ya da sağ taraftaki “show plot tools and dock figure”
butonuna basabilirsiniz.
Şekil 3: Şekil özelliklerini değiştirme
Şekil 3’teki gibi elde ettiğiniz grafiğin görsel özellikleri ile oynayabilir, daha sonra istediğiniz formatta
kaydedebilirsiniz “save as” diyerek. .fig uzantılı dosyalar, tekrar bu pencere ile açmaya dolayısıyla
daha fazla değişiklik yapmaya ve değerleri okumaya izin verir.
Özel çözüm önerip, A1, A2,B1,B2 değerlerini bulalım.
1
1
0
1
1
1
1
0
0
1
1
1
1
0
1
1
A1
A2
B1
B2
1
0
0
1
Denklem takımını MATLAB kullanarak çözelim.
Ax=[-1 -1 0 1; -1 1 1 0; 0 -1 -1 -1; -1 0 -1 1];
b=[-1; 0; 0; -1];
AB = inv(Ax)*b
command window’da karşımıza çıkan sonuç:
AB =
0.4000
0.2000
0.2000
-0.4000
Özçözümü bulduğumuz gibi özel çözümü de bulabiliriz:
x_ozel_0=[AB(2); AB(4)];
for T=1:100;
t=T/10;
x_tam(:,T)=[ov(:,1)*exp(od(1)*t) ov(:,2)*exp(od(2)*t)]*M_0_ters*x_0 +
[AB(1)*sin(t)+ AB(2)*cos(t); AB(3)*sin(t)+AB(4)*cos(t)] -[ov(:,1)*exp(od(1)*t)
ov(:,2)*exp(od(2)*t)]*M_0_ters*x_ozel_0;
end
figure;
plot(x_tam(1,:));hold all; plot(x_tam(2,:))
Fazör kavramından yararlanarak
Öncelikle kaynakları ve açısal frekansı tanımlayalım:
w=1;u=[1/sqrt(2); -i/sqrt(2)];
1 olarak tanımlıdırlar. Bir sayının karekökünü
i ve j eğer kod içinde başka şekilde atanmadılarsa
almak için sqrt(sayı) ya da sayı^(1/2) komutları kullanılabilir. Çözümü bulabilmek için, U ikiye ikilik
birim matris olmak üzere,
x = (jwU-A)-1Bu
işlemini aşağıdaki şekilde yapabiliriz:
x=inv(i*w*eye(2)-A)*B*u;
Burada birim matris eye(2) komutu ile tanımlanmıştır. (ara: identity matrix)
İşlemin sonucunda 2 elemanlı bir sütun vektör elde edilir. Birinci eleman x1, ikinci eleman ise x2 olur:
x1=x(1);
x2=x(2);
Bu iki karmaşık sayının genliği ve açısı kullanılarak işaretin efektif değeri ve fazı elde edilebilir:
X1=abs(x1);faz1=angle(x1);
X2=abs(x2);faz2=angle(x2);
Şimdi tek yapmamız gereken yukarıdaki değerler ile bir kosinüs eğrisini zamanın fonksiyonu olarak
çizdirmek. Bunun için bu defa bir for döngüsü kullanmak yerine, öncelikle bir t vektörü
tanımlayabiliriz.
t=0:0.1:10;
figure;
plot(sqrt(2)*X1*cos(w*t+faz1));hold all;
plot(sqrt(2)*X2*cos(w*t+faz2));