Deneysel yoldan belilrlenen kovaryans fonksiyon, gerçek fonk.
siyondan az çok sapar. Dengeleme hesabında ağırlıkların ve korelasyonların hatalı alınmasının dengeleme sonuçlarına etkisine koşut
olarak, kollokasyonda da hatalı kovaryans fonksiyonun Sj sinyal değerine etkisi sapmaların 1. dereceden, varyansına etkisi sapmaların
2. dereceden fonksiyonları büyüklüğündedir.
7.
SAYISAL UYGULAMA
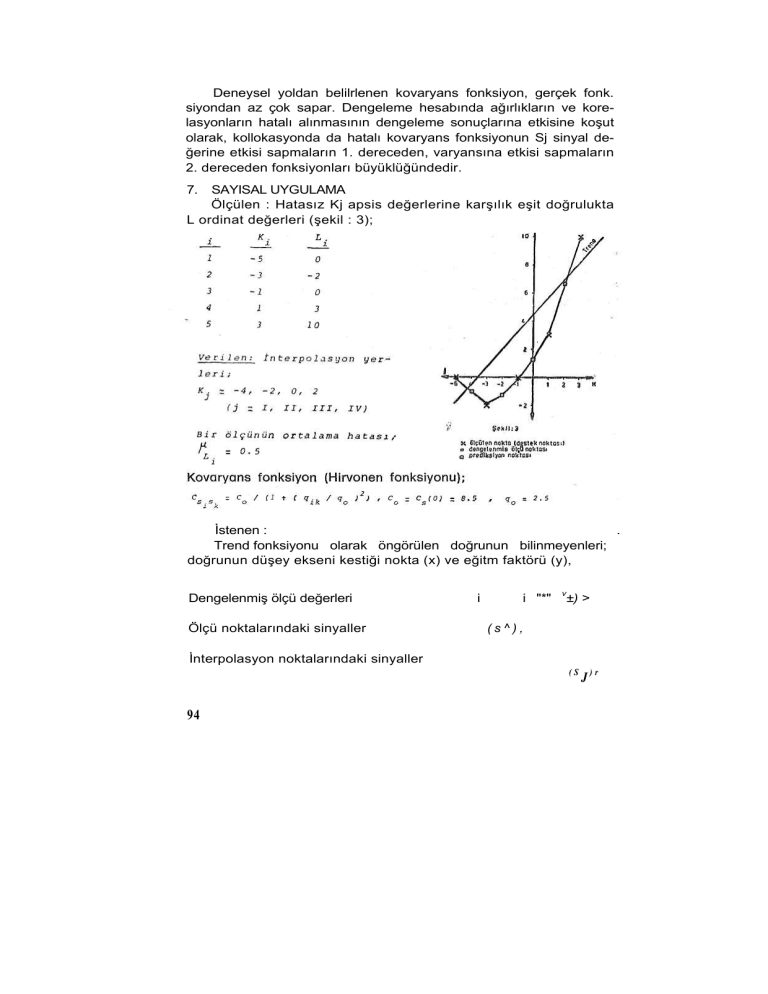
Ölçülen : Hatasız Kj apsis değerlerine karşılık eşit doğrulukta
L ordinat değerleri (şekil : 3);
İstenen :
.
Trend fonksiyonu olarak öngörülen doğrunun bilinmeyenleri;
doğrunun düşey ekseni kestiği nokta (x) ve eğitm faktörü (y),
Dengelenmiş ölçü değerleri
Ölçü noktalarındaki sinyaller
i
i "*"
v
±) >
(s^),
İnterpolasyon noktalarındaki sinyaller
(S
94
J)r
95
Hesaplanan büyüklüklerin ortalama hatalarını elde etmek için,
onlara ilişkin ağırlık katsayıları matrisleri hesaplanmalı ve sonra bu
matrislerin köşegen elemanlarının kareköklerl m0 değeriyle çarpıl,
malıdır, (bak. 4)
96
97
K A Y
N A K Ç A
Assmus E./Kraus, K. 1974) :
Dle İnterpolation nach kleinsten Quadraten, Prâdiktionswerte simulierter Beisplele
und ihre Genauigkeiten. DGK, Nr, 76
Demirel, H. (1977)
:
En Küçük Kareler Yöntemine Göre Prediksiyon ve Kollokasyon. İDMMA, İstanbul.
Moritz, H. (1973)
:
Least-S|quares Collection.
Nr. 75.
Reissmann, G. (1979)
:
Die Kollokation; Ein allgemeinstes Ausgleichungsverfahren. Vermessungstechnik, Heft
1, s. 7-12.
Ulsoy, E. (1974-1975)
:
Yeni Dengeleme ve Prediksiyon Yöntemleri.
Harita ve Kadastro Mühendisliği Dergisi,
Sayı 31-32, s. 701-709; Sayı 35, s. 1-7.
Wolf, H. (1974)
:
Über verallgemeinerte
Heft 2, s. 475-478.
Wolf H. (1977)
:
Die Sonderfaelle der diskreten Kollokation.
Österr. Zsch. f. Verm., Heft 314, s. 132-138.
Wolf, H. (1979)
:
Kollokation mit Hilfe des Gausschen
Algorithmus. ZfV. Heft 1, s. 2-19.
98
DGK, Reihe A,
Kollokation. ZfV,
JEODEZİDE OLASI DÜŞÜNCE
Doç. Dr., .Onur GÜRKAN
Karadeniz Teknik Üniversitesi
Cümle yaratılmışa Birlik
ile bakmayan Halka
müderris ise Hakikatte
asidir.
Yunus Emre
1 — G İ R İ Ş
Belirli çevrelerde kuram (teori) soyutla, kılgı (pratik) somutla
özdeşleştirilir. Kuşkusuz bu, olumsuz bir koşullanmanın ürünüdür.
Çünkü böylesi bir düşünce zihinlerinde doğma haline gelenlerin gözüne kuram (teori) ile kılgı (pratik) biribirinin alternatifi olarak görünür. Daha açık bir deyişle, bunlara göre; kuram (teori) ile kılgı
(pratik), birisinin bulunduğu yerde ötekinin bulunmaması gereken
düşman kardeşler gibidir, birisinin yararına olan ötekinin zararınadır, birisinin yaptığını öteki bozar, vb.
Oysa, çağımızın en geçerli ve gerçekçi düşünce sistemi olan
pragmatik yaklaşımda, kuram (teori) ile kılgı (pratik) bunun tam tersi
bir görünüm içindedir, ve bunlar olumlu sonuca götüren her planlı
ve organize faaliyette birlikte işlevleri olan iki partner gibidir. Kuramı
(teoriyi) yeterince değerlendirmeyen bir kılgıyla (pratikle) ya da
kılgıyı (pratiği) dışlayan bir kuramla (teoriyle) tasarlanan ve yürütülen bir faaliyetin belirli düzeyi aşan ve sürekliliği güvencede olan
bir başarıya ulaşma şansı çok azdır.
Bilindiği gibi modern anlamda en küçük bir faaliyetin bile tasarımının yapılabilmesi, planlanıp organize edildikten sonra yürütmeye
konabilmesi, yürütmenin izlenebilmesi, denetlenebilmesi vb. için incelemeler, çözümlemeler, araştırmalar, denemeler vb. yapılmalıdır.
C/S9
İşte bu inceleme, çözümleme, araştırma, deneme, vb.'lerînden
amaç, kuram (teori) ile kılgının (pratikliğin) bir bütünlük içinde değerlendirilmesidir. Bir başka deyişle, bunlardan amaç, faaliyette işlevinin bulunması olasılığı olan tüm nesne ve olayların karşılıklı doğal etkileşimlerini aralıksız saptamaktır. Böylece, tasarımlama yapılırken doğaya uymayan düzenlemelerin getirilmesinden ve kuralların
konmasından olabildiğince sakınılmış olunur; dahası, herşeye karşın
sakınılamamış olanlar varsa, yürütmenin izlenmesi ve denetlenmesi
aşamasında bunlar anında tanınarak önlem alma yoluna gidilebilir.
İncelemeler, çözümlemeler, vb. yapılmaksızın, deneyimli de olsa
bir ya da birkaç kişinin yalnızca sezgilerine dayanılarak tasarımlanan, yürütmesi izlenen, denetlenen, vb. bir faaliyetin çağdaş ve gerçekler karşısında etken olmasını beklemek, aklın üstünlüğünün gözardı edilmesi anlamına geleceği açıktır. Öte yandan, ortada gereksinimlerden kaynaklanan, bir öngörü biçiminde bile olsa, bir faaliyet
ya da sorun yokken salt bilimsel vb. dürtülerle doğa gerçeklerini
tanımaya dönük inceleme, çözümleme, araştırma, deneme, vb.'ni
yapmaya girişmek de en azından çağın ve toplumun gerçeklerinin
dışında bir «düşler dünyası»nda yaşayanlar olduğunun kanıtı sayılmak gerekir.
Buradan, inceleme, çözümleme, araştırma, deneme, vb.'den hiçbirinin çağımızda artık yalın kuramsal (teorik) amaçiar için yapılmadığı (daha doğrusu böyle bir amacın, özellikle gelişmekte olan toplumlar açısından, anlamsızlığı), tam tersine bunların ana amacının
kılgı (pratik) olduğu, ancak yöntemlerinin bilimsel, sonuçlarının da
kurama (teoriye) ilişkin olması gerektiği vurgulanabilir.
2 — FİZİKSEL VE MODEL ÇEVRELER
İnceleme, çözümleme, araştırma, deneme, vb.'nin yönteminin
bilimselliğinden kasıt, doğanın öngördüğü sistemli bir ele alışın ilke
olarak benimsenmesidir. Bunun için iki çevre kavramı ile bunların
arasındaki çelişkilerin yorumu söz konusudur.
Fiziksel çevre : İnceleme, çözümleme, vb.'nin kapsamına giren
tüm nesne ve olayların kendileri fiziksel çevreyi oluşturur. Bir başka
tanımlamayla, bu çevre doğa'nın tam kendisidir.
Model çevre : İnceleyicinin, araştırıcının, vb.'nin bilgi düzeyi, deneyimleri, sezgileri, algılamaları, vb. gibi kendi öznel olanakları ile
100
fiziksel çevreye benzeterek tasarımladığı bir modeldir. Bu model
fiziksel çevrenin belli ölçekteki yapay bir benzeri olabileceği gibi,
bir harita, bir plan, bir çizelge, bir grafik, bir fonksiyon, bir tanım vb.
de olabilir. Kısası, model "çevre, fiziksel çevreye bir yaklaşımdır ve
kişilerin düşüncelerinin bir ürünüdür.
Çelişkiler : Yapslan gözlemlerle, bu ikisi arasındaki çelişkiler
saptanarak yorumlanır ve kurulmuş olan model, olabildiğince (istenen İncelik, doğruluk - güvenirlik ve ekonomiyle) ' fiziksel çevreye
yaklaştırılmak üzere düzeltilir.
Jeodeziden iki örnek :
1) Bir gökcismi olan yeryuvarının kendisi fiziksel çevredir.
Düzlem gibi düşünüldüğü dönemler bir yana bırakılırsa, yeryuvarının
biçimi için ilkin bir küre düşünülmüştür. Yüzyıllar boyunca da bu
modelin fiziksel çevreye özdeş olduğu varsayılmıştır (Hâlâ bazen
yerküresi deyimi kullanılmaktadır). Ancak, zamanla, yapılan gözlem
lerden çıkarılan çelişkiler bu varsaytrnı geçersiz kılmaya başlamıştır.
Çelişkilerin yorumlanmasıyla da yeryuvarı için kutuplarda basık bir
dönel elipsoidin, küreye göre biraz daha geliştirilmiş bir model oldu
ğu belirlenmiştir.
2) Yeryüzünde işaretlenmiş üç noktanın (nirengi noktalan) bir
referans yüzeyine izdüşürülmeleriyle oluşan üçgen, fiziksel çevredir.
Anılan referans yüzeyinin düzlem olduğu varsayımıyla iç açılar top
lamının 200 g kabul edilmesi, bir model çevre tasarımıdır. Öte yan
dan eğer üçgenin kenarları yeterince büyükse (referans yüzeyinin
artık bir düzlem varsayılamayâcağı oranda büyükse) ve eğer hiç
gözlem hatası yapılmadan iç açılar ölçülürse, bunların toplamının
200 g'dan hep fazla çıktığı görülür. İşte bu fazlalık, tasarımlanan
model çevreye ilişkin bir çelişkidir ve çok iyi bilindiği gibi de ekses
olarak yorumlanması gerekir.
Çelişkilerin yorumlanması : Bu konuda iki temel düşünce sistemi yardımcı olur. Bunlardan birisi gerekir (deterministle), ötekisi de
olası (probabilistic) düşüncedir. Eğer çelişkiler, görünen sonuçlar
olarak ele alınıp neden.sonuç ilişkileriyle nedenlere, inilirse, bir baş.
ka deyişle, bu çelişkileri doğuran nedenler bulunup teşhis edilirse,
gerekir (deterministte) bir düşünce yolu izlenmiş derrtefcür. Yukarıdaki
iki örnekte de yorumlama böylesi bir düşünüşle becerilmiştir.
Çelişkilerden bu yolla ortaya konabilen nedenler, model çevre tasa101
rımlcımrken dikkate alınmayan ama fiziksel çevrede var olan parametrelerdir. Dolayisıyle bunların fiziksel çevredeki tanımları açık seçik bir biçimde verilebilmelidir. Yukarıdaki örneklerin ilkinde bu,
basıklık paramatresidir (ya da küre için bir tek olan yarıçap yerine,
dönel elipsoid için iki yarıçaptır); ikincisinde ise eksestir (ya da referans yüzeyin sonlu ve belirli eğriliğidir). Olası düşüncede de, görünen sonuçlar olarak çelişkiler yine parametreler biçiminde verilir,
ancak bu kez bunlar fiziksel çevrede açık seçik tanımlanabilen nedenler olarak sunulamaz. Çünkü, bu düşünce sisteminin özünde ve
uygulanan işlemlerde nedenlerle ilgilenmek gibi bir olgu yoktur. Burada, olasılık yasaları yardımıyla çelişkiler istatistik parametrelere
dönüştürülüp anlamlılık düzeyleri konusunda kararlar, daha doğrusu
karar almaşıkları üretilir. Anlamlı bulunanların fiziksel çevrede tanımlanabilen birer neden olarak yorumlanabilmesi için, hem genellikle ek bilgilere gereksinim duyulur, hem de bu, yine ancak gerekir
(deterministic) bir düşünüşle becerilebilir.
3 — OLASILIK, RASTGELG DEĞİŞKEN, RASTGELE FONKSİYON,
KESTİRİM ¥E KARAR KURAMLAR!
Olasılığın tanımını, tarihsel bir çizgi boyunca geçirdiği değişimlerle kısaca vermek, bazı kavramların anlaşılmasını kolaylaştıracaktır.
Ancak, bunlara geçmeden önce de «deney», «deneme», «olay» sözcüklerinin sonraki kullanılış anlamlarını açıklamada yarar vardır.
«Deney» üç ana öğeden oluşur. Bunlar, olasılık uzayı, «olay»lar
ve olaylara tahsis edilen olasılıklardır. Örneğin; bir tek zarın bir kez
atılması deneyinde olasılık uzayı S = { 1, 2, 3, 4, 5, 6 I- biçiminde
altı elemanter olaydan oluşmaktadır. Olaylar ise, a = --i çift \ ■■=
•■I 2, 4, 6 [ , b = -i tek I = -i 1, 3, 5, \, vb. gibi elemanter olaylarla
tanımlanan ve olasılık uzayının birer alt kümesi olan kümelerdir.
Tahsis edilen olasılıklar d a P - M İ - = P -i 2 !■ = P -i 3 }■ = P | 4 [ =
. P { 5 } = P 1 6 } = 1/6
gibi bir sıfır ile bir arasında değişen sayılardır. «Deneme» de deneyin bir kez sınanmasıdır.
Â) İnanış ölçütü olarak olasılık : En eski olasılık tanımıdır ve
somut bir kanıt olmaksızın kişinin öznel sezgilerine, koşullanmalarına, deneyimlerine, vb. bağlı bir hüküm niteliğindedir. Örneğin, «Bu
yarışmada X'ın kazanacağına inanıyorum» diyen birisi, yarışmacılar
arasında X'ıri birinci gelme olasılığının, öteki yarışmacılardan her.
102
hangi birisinin birinci gelme olasılığından daha fazla olduğuna inanmaktadır ve tahsisini öyle yapmaktadır. Öznel bir ölçüttür, kişiden
kişiye değişebilir.
B) Klasik tanımıyla olasılık : Bir deneyi tanımlayan olasılık
uzayındaki tüm elemanter olayların sayısı N, olasılığı aranan (a) ola
yındaki elemanter elemanların sayısı Na ise, (a) olayının olasılığı
p(a)
=
. --------N .
olarak belirlenir. Yukarıda anılan örnekte; N = 6, Na = 3 olarak
P(a) = Pl çift }■
3
= P t 2, 4, 6 r = ----- = 0,5
6
bulunur. Burada tüm elemanter olayların olasılıkları biribirine eşit
varsayılmaktadır. Ayrıca, bu tanım her deneye uymayabilir.
C) Göreli yineleme tanımıyla olasılık : Bir deneyde n kez dene
me yapılır, (a) olayı na kez ortaya çıkarsa, bunun olasılığı
na
P (a) = ----n
ile belirlidir. Yine yukarıda anılan örnekte; zar n = 1000 kez atılmış
ve bunlardan na = 403'ünde zarın 2, 4, 6 yüzlerinden herhangi birisi
gelmişse, bir başka deyişle -i çift \ olayı ortaya çıkmışsa,
483
P (a) = P \ çift \ = P i 2, 4, 6 i- = -------- = 0,493
1000
bulunur. Kolayca görüleceği gibi klasik tanımdan farklıdır. Olasılıklar düşünsel olarak değil denemelerle bulunmaktadır. Ancak bu tanımın geçerliliği de n deneme sayısının sonsuza yaklaşmasıyla
mümkündür.
D) Aksîyomatik tanımla olasılık : En son aşamadaki tanımdır
ve yukarıdakilere karşı öne sürülen haklı tüm itirazları geçersiz kı
lar. Bu tanımda herkesin tartışmasız kabulleneceği üç aksiyom or
taya konmakla yetinilir. Bu üç aksiyom şunlardır :
103
... Bir deneyde tanımlanacak olayların olasılıkları daima {+}
artı işaretlidir;
*
P (a) Jî 0, ;!
uzayının olasılığı Ve eşittir;
... Bir deneyin olasılık
P (S) = 1 ,
... Bir deneyde tanımlanan olaylardan biribirini dışlayan iki olayın toplam olasılığı, bu olayların olasılıklarının toplamına eşittir;
(a) ile (b)'nin biribirlerini dışlamaları koşuluyla,
P (a+b) = P (a) + P (b).
olur.
Karşılaşılan probleme, mevcut bilgi ve olanaklara göre günümüzde bunlardan birisi ya da yer yer birkaçı birarada kullanılmaktadır. Burada, herhangi birisine bağlı kalınmadan olasılığa ilişkin
öteki bazı temel kavramlardan da söz edilecektir.
Rastgele değişken kavramı, olası düşünceyle türetilen model
çevrede istatistiğe ilişkin işlemlerin çekirdeğini oluşturur. Bu kavrama da yukarıda sözü edilen deney, olay ve deneme tanımlarından
geçilecektir, Bir deneyin olasılık uzayı şekil Tde görülene benzer bir
diyagramla temsil edilebilir. S = \%î,Z > 2,...\ olasılık uzayının her
elemanter olayı %i, bir noktayla gösterilmiştir. Bunlar x=x (%) gibi
bir kuralla sayıya dönüştürülerek yönlü bir doğru üzerinde gösterilebilirler. Kurala göre farklı iki ya da daha fazla %, x ekseni üzerinde
104
aynı noktayı da işaret edebilir. Ayrıca, S olasılık uzayının elemanter
olayları (elemanları)ndan belli bazıları ile a = -!£2,-Ç2, Ç4K vb., gibi
olaylar tanımlanır ve bunlar yukarıdaki, dönüşümle a = -I x ^ xa>
olacak şekilde bir düzenleme yapılabilir. Ayrıca % ekseni üzerindeki
bir noktaya karşılık filerden ne kadar düşüyorsa ona göre eksenin
her noktasının bir yoğunluğu olacaktır. Bu da a = i x ^ x a } olaylarının olasılıklarını tanımlamada kullanılabilir. Kısası bir deneyi tanımlayan S olasılık uzayı, a olayları ve bu olaylara tahsis edilecek P (a)
olasılıklarının tümü, istenirse x gibi bir değişken yardımıyla matematik anlamda formülüze edilebilir. İşte buna rastgele değişken denir.
Rastgele denmesinin nedeni, bir denemede belli bir^i elemanter
olayının ortaya çıkması, dolayısiyle ona karşılık olan x değeri ile
karşılaşılması tamamen rastgele olmasındandır. Bunun olasılığı da
x ekseninin yoğunluk dağılımına bağlıdır. Dolayısiyle her rastgele
değişken için bir dağılım tanımlamakla, olaylara olasılık tahsis etmek eş anlamlı olur. Bu şöyle becerilir;
... Öyle bir F(x,)-fonksiyonu tanımlansın, ki bununla a = ■! Cxa ^
biçiminde tanımlanacak bir (a) olayının P (a) olasılığı
P (a) = P i x ^ x a ^ = F (x a )
olarak tahsis edilmiş olsun,
... Yukarıda sözü edilen aksiyomlarla uyumlu olabilmesi için de
F (x) fonksiyonunun
F { — oo) = 0, F (+ oo) = 1 , xi ^x, için F (xı) < F (x;)
özellikleri bulunmalıdır.
... f (x) fonksiyonu x ekseninin yoğunluğunu (eksenin her noktasına Çelerden ne kadar düştüğünü) gösteriyorsa
xa
FW-Tf(x)dx
--
bağıntısı olmalıdır ..
oo
;
Uygulamalarda çeşitli dağılımlardan söz edilir ama bunlardan
üçünün ayrı önemi vardır.
Binom (Sağılımı ; x rastgele değişkeninin k = 0, 1,2, ..., n gibi
sonlu sayıda diskrît değerlerden herhangi birisini alması durumunda
uygulanabilir ve dağılım fonksiyonu
105
olarak belirlidir. Burada p ilgilenilen a olayının bir denemede ortayG
çıkma olasılığı, n de deneme sayısıdır. S ise ünlü impuls fonksiyonudur. Görüldüğü gibi burada hem dağılım hem de yoğunluk fonksiyonu deneme sayısına bağlıdır.
Bu dağılımın parametreleri p ve n olup, bir örnek olmak üzere p
= 1/2, n = 9 ile f9 (x)'ın grafiği şekil : 2'de verilmiştir.
Porsson dağılımı : x rastgele değişkeninin 0, 1, 2, ..., n, ... gibi
sonsuz sayıda diskrit değerlerden herhangi birisini alması durumun,
da uygulanabilir ve dağılım fonksiyonu
F ( k | = P f x = k}
106
—X
= e
Xk
---- ; k = 0, 1, 2 ............ X> 0
k!
107
İstenirse aynı olasılık uzayını oluşturan elemanter olaylar y=y (y)
gibi bîr başka kuralla yine sayıya dönüştürülerek bir başka yönlü
doğru, dolayısiyle bir başka rastgele değişken tanımlanabilir. Kuşkusuz bunun da kendine özgü F (y) gibi bir dağılım, f (y) gibi bir yoğunluk fonksiyonu olacaktır.
Bazı problemlerde hem x=x (£), hem de y=y (£) dönüşümlerine
gereksinim duyulabilir ve böylece olasılık uzayının herhangi bir Ej
elemanter olayı x ve y eksenlerinin oluşturduğu düzlemde bir noktaya karşılık gelir. Olaylar da bu kez c = -i x ^xa, y■< yb \ biçiminde
tanımlanır. Her elemanter olaya düzlemin bir noktası karşılık geldiğinden bunlarla tanımlanan olayldr da düzlemin bir parçasına karşılık gelir. Dolayısiyle tahsis edilecek olasılıkları veren dağılım fonksiyonu da F (x,y) biçiminde olmalıdır. Düzlemin her noktasına ne kadar elemanter olayın düştüğünü tanımlayan yoğunluk fonksiyonu da
f (x,y) biçiminde olur. Bunlara birleşik dağılım ve yoğunluk fonksiyonları denir. Örneğin, normal dağılımlı-x ve y rastgele değişkenlerinin birleşik yoğunluk fonksiyonu
olarak belirlidir. Burada, T)X ve Cx sabitleri x rastgele değişkenine,
Tjy ve C> de y rastgele değişkenine ilişkin parametrelerdir, r ise bu
iki rastgele değişkenin aralarındaki karşılıklı istatistik ilişkiyi veren,
sıfır ile bir arasında değerler alabilen korelasyon katsayısıdır ve bir
anlamda bu da bir parametredir.
Problemin gereği aynı olasılık uzayından ikiden çok rastgele değişken türetilmesi de söz konusu olabilir. Bu durumda artık çok boyutlu bir uzay söz konusudur ve olaylar, matematik anlamdaki bu
soyut uzayda tanımlanarak F (x, y, z, ...) ve f (x, y, z,...) birleşik dağılım ve yoğunluk fonksiyonlarıyla bunlara tahsis edilecek olasılıklar
formülüze edilebilir.
Bazen de aynı olasılık uzayından iki grup halinde L = (I,, h,.., IJT
ve X = (Xı, x2,..., xu)T gibi iki ayrı rastgele değişken dizisi tanımlanabilir. Eğer bu dizilerden her biri olasılık uzayının tümünü kapsıyorsa, bir başka deyişle; herbir dizi fiziksel çevreyi tek başına tasarım108
layan bir model çevreyse, gerekir (deterministle) düşünceye göre bu
dizilerin arasında önceden belirli X=X (L) ya da L=L (X) = X (X)
gibi bir dönüşüm bağıntısı olmalıdır, (Şekil : 5). Dolayısiyle bu dizi
lerden birisinin İtim istatistik parametreleri ve bu gerekir (determi
nistle) dönüşüm bağıntıları ile öteki rastgele değişken dizisine ilişkin
tüm istatistik parametreler bulunabilir. Bu olgu, gerekir (deterministic) ile olası (probabilistic) düşüncelerin nasıl bütünleşebildiklerinin
bir kanıtıdır.
. . , :
.
L ve X, ve araİGrındaki dönüşüm X—X (L) , L= X— 1 (X)
İstatistik kestirim (estimation) kuramı şu üç ana başlığı kapsar.
Â) Bir rastgele değişkenin ya da rastgele değişken dizisinin
parametrelerinin gözlemlerden doğrudan doğruya bulunması (kestirilmesi),
B) Bir rastgele değişkenin ya da değişken dizisinin parametrelerinin aralarındaki gerekir (deterministic) dönüşüm bağıntıları önceden bilinen bir başka rastgele değişken ya da değişken dizisinin
parametrelerinden dolaylı olarak bulunması (kestirilmesi),
109
C) Parametreleri bilmen iki rastgele değişken ya da değişken
dizisi arasındaki gerekir (deterministte) bağıntının bulunması (kestirilmesi). Kurumla (teoriyle) kılgı (pratik) arasındaki köprüyü de buradaki kestirim (estimation) kavramı kurmaktadır. Çünkü, bir rastgele değişkenin parametrelerinin olasılık uzayından doğrudan doğruya
ya da dolaylı olarak belirlenebilmesi, kuramsal anlamda sonsuz sayıda gözlem yapmayı gerektirir. Oysa, pratikte bu olanaksızdır. İşte
bu çatışma, olasılık uzayından çekilen ve hem sonlu sayıda gözlemle altından kalkılabilen, hem de olasılık uzayını temsil etmesi beklenen örnek kümeler yardımıyla önlenir. Bu işlem bir kestirimdir, tahmin yapmaktır.
İstatistik karar kuramı ise kısaca, kestirilen parametrelerin ya
da dönüşüm bağıntılarının istatistik anlamlılık düzeylerinin istatistik
testlerle kestirimi olarak tanımlanabilir. Bununla, kuramla (teoriyle)
kılgı (pratik) arasına kurulmuş olan köprü sağlamlaştırılmış olunur.
Aşağıdaki örneklerin bu açıklamaları daha da aydınlık kılacağı
umulmaktadır. Jeodezide bir nesnenin büyüklüğünün (açı, uzunluk,
vb.) yinelemeli olarak gözlenmesi, onun bir rastgele değişken olarak ele alınması anlamınadır. Yinelemeli gözlemlerle, rastgele değişken için bir örnek küme çekilmiştir. Eğer rastgele değişkenin normal
dağılımda olduğu varsayılarak bu örnek kümeden bir ortalama ve
bir karesel ortalama hata hesaplanırsa, bunlar rastgele değişkenin
sırasıyla TJ (umut değeri) ve <r (standart sapma) parametrelerinin
kestirilmiş değerleri olur. Burada ayrıca, çekilen örnek kümenin olasılık uzayını temsil yetkisinin bulunduğu ve radtgele olduğu varsayılmıştır. Burada yapılmış olan işi istatistik kestirim kuramının bütünlüğü içinde tanımlamak gerekirse, buna, «en küçük karelerle doğrusal parametre kestirimi» demek daha doğru olur. Öte yandan şekil
5'de temsilî olarak verilen L = (llf 12,.,., IJT rastgele değişken dizisindeki herbir bileşen bir nirengi ağındaki gözlenmiş doğrultu.ve
kenarlardan birisi, X = (x,, x2,..., xn)T rastgele değişken dizisindeki
herbir bileşen de o ağdaki noktaların koordinatlarından birisini göstermiş olsun. Bilindiği gibi gözlemleri temsil eden L vektörünün
herbir bileşeni için önce parametreler (T) , C , r
kesin değerler,
■I, I, I.. I,
karesel ortalama hataları ve korelasyonlar olarak) kestirilir. Ddha
sonra, Jeodezicilerin mekaniğini çok iyi bildikleri «en küçük kareler110
le dengeleme hesabı» ile bu parametreler X vektörünün herbir bileşeninin (Tİ , er , r ) parametrelerine dönüştürülür. İstatistik
X;
Xı
XİX;
kestirim kuramına göre bu da bir <;en küçük karelerle doğrusal parametre kestirimisdir. Burada L vektörü ile X vektörü arasındaki gerekir (deterministle) bağıntı geometri teoremlerine göre kurulmaktadır. İstenirse peşpeşe uygulanan bu iki kestirirn işlemi bir
tek adımda da becerilebilir. Bunlar, istatistik kestirim kuramının ilk
iki ana başlığında içerilmektedir. Jeodezicilerin yine çok yakından
bildikleri «en küçük karelerle dengeli fonksiyonların belirlenmesi»
de yukarıdaki başlıklardan üçüncüsünde içerümektedir. Ancak, bu
üçüncüsünde genellikle dönüşümün tipi önceden sezgisel olarak
saptanarak, bunu gerçekleyecek bağıntıların katsayılarının istatistik
parametrelerinin kestirimi yapılır. Bir başka deyişle uygulamada parametre kestirimi kavramı yukarıdaki üç ana başlığın üçünün de özünü oluşturmaktadır.
Kestirilen parametrelerin tümünün de bazı varsayımları -içermiş
olması herşeyden önce bu varsayımların gerçeğe yaklaşım oranlarımn da bilinmesini gerektirir. Bu da yine istatistiğin karar kuramına
ilişkin varsayım testleriyle becerilir. Bu kuramın tüm işlemlerinin
özünde de olasılık yatar ve testlerin sonuçlan (kararlar ya da karar
almaşıkları) belli bir olasılıkla anlamlılık düzeyleri olarak verilir. Ancak varsayım testlerinin kendilerinin de birer varsayımın ürünü olduklarını burada vurgulamakta yarar vardır. Elde edilmiş bir model
çevreyle, asıl ele alman fiziksel çevrenin uyuşumlarına ilişkin karar
üretiminde, yeterince kuramsal ayrıntıya inilmezse yanıltıcı pratik
sonuçlar alınabilir. Bu olgu da kuramla (teoriyle) kılgının (pratiğin)
içiçeliğini sergileyen güzel bir örnektir.
Başlangıçta olasılık uzayını oluşturan her elemanter Ç olayı
x = x (£) gibi bir kuralla skalar bir büyüklüğe dönüştürülüp
yönlü bir doğru üzerinde gösterilerek rastgele değişken kavramı
verilmişti. Oysa bazı problemlerde bu da yetersiz kalabilir ve olasılık
uzayının her ©lemanter ^ olayı Xj (t) = x (t, £,) biçiminde t gibi bir
başka değişkene bağlı bir fonksiyon olabilir. Bu durumda artık rastgele değişkenden değil, rastgele fonksiyondan (stokastik süreçten)
sözedilir.
111
Şekil : 6'da görüldüğü gibi artık bir fonksiyon ailesi söz konusudur, tj = t için bu aile x (tj, Ş.) = Xj (%) — Xj olarak bir rastgele değişken vermektedir, t/nîn, — oo'dan + oo'a kadar değerleri için sonsuz sayıda bileşeni olan rastgele değişken dizisi vardır. İşte stokastik süreçlerle ilintili tüm kuramsal temeller, bu sonsuz sayıda bileşeni olan rastgele değişken dizisinin birleşik dağılım ve yoğunluk
fonksiyonunun üstüne kurulur. Dolayısiyle yukarıda anılan istatistik
kestirim ve karar kuramları biraz daha karmaşıklaşmış bir biçimde
stokastik süreçlerde de kendi pratiklerini bulurlar.. , .
Stokastik süreçlerin jeodezideki uygulamalarına örnekler olarak
ilk ağızda baraj deformasyonları ile yerkabuğu hareketlerinin jeode.
zik yöntemlerle izlenmesi verilebilir. Eğer yukarıda şekil 5'de görülen L ve X dizilerinin, fikiksel çevredeki anlamları saklı tutularak, herbir bileşeni zamana da bağımlı olarak modellendirilirse, bunlar L (t) ='[!.!. (t), l2 (t),..., ln (t)]T ve X (t) = [x, (t), x2 (t),..., xu (t)F
biçimine girerler. Bu bilimleriyle bunlar da sîokastik süreçten başka
bir şey değillerdir.
", 4 — JEODEZİNİN İÇERİĞİ Jeodezi mesleği görev
üstlendiği: tüm faaliyetlerde
... Ölçüler yaparak, belgeler tarayarak, kişilerle görüşerek, vb. yollarla VERİ TOPLAR;
112
... Hesaplayarak, çizerek, karşılaştırarak, sınıflandırarak, ayırarak,
birleştirerek, süzerek, vb. yollarla TOPLANAN VERİYİ İŞLER;
... Kütükler, kayıtlar, çizelgeler, harita ve planlar, belgeler, raporlar;
matematik fonksiyonlar, yeryüzü işaretleri vb. biçimlerde İŞLENMİŞ VERİYİ SERGİLER,
Bu içerik yukarıdaki açıklamaların ışığında ele alındığında, kütük, kayıt, çizelge, harita, plan, belge, rapor, matematik fonksiyon,
vb. biçimde sergilenen işlenmiş verinin, belirli bir fiziksel çevre için
tasarımlanıp üretilen model çevreyi oluşturduğu söylenebilir. Öte
yandan, hazırlanmış bir projenin bir model çevre olarak değerlendi,
rilmesi durumunda aplikasyon işlemiyle sergilenen yeryüzü işaretleri
yaratılmış bir fiziksel çevreyi oluşturur.
Buradan, «Jeodezinin içeriği, belirli bir fiziksel çevre için bir
model çevre tasarlayarak bunu üreten, ya da üretilmiş bir model
çevreye uyan bir fiziksel çevre yaratan bilgi ve becerilerin tümüdür»
biçiminde bir tanım verilebilir.
Verinin toplanması, işlenmesi ve sergilenmesi aşamalarında
başvurulan bilgi ve becerilerde kuram (teori) ile kılgının (pratiğin)
içiçeliğinin bir öneeki bölümde özlü ama oldukça açık olarak ortaya
konduğu savunulabilir. Örneğin, yeryüzünde işaretlenen nirengi noktaları, fiziksel çevrede günlük yaşantıya ilişkin pratiğin gereksinimlerini karşılarken, bunları tamamlayan abrisler, koordinat çizelgeleri
vb. de kuramın bir gereğidir. Aynı örnekte gerekir (deterministio) ve
olası (probalistic) düşüncelerin biribiriyle ne denli bütünleştiklerini
de görmek mümkündür. Nirengi noktalarının yeryüzüne işaretlenmeleri, bunları biribirine bağlayan gözlemlerin planlanmaları, oluşan
şekillerin geometrilerinin kurulması, vb.'de gerekir (deterministle)
düşünce sistemi nasıl vazgeçilmez bir araçsa, gözlemlerin yinelenmesinde, bunların birer rastgele değişken ya da stokastik süreç olarak ele alınıp parametrelerinin kestirilmesi, sonra da noktaların
koordinatlarının bir dönüşümle bunlardan birer rastgele değişken
ya da stokastik süreç olarak türetilmelerinde de olası düşünce o
denli gerekli bir araçtır. Son yıllara değin adları kullanılmamış olsa
da zaten rastgele değişken ve bunun parametreleri yüzyıla yakın bir
süredir jeodezinin teori ve pratiğinde, gerekir (deterministte) düşünüşlerin içinde yerlerini almışlardır. Tek boşluk, meslek çevrelerinde
olası (probabilistie) düşünüşün özünün yeterince bilincine varılamamış olmasıdır. Son yıllarda stokastik süreç kavramının da kapıyı zor113
laması sonucu gerekir (deterministte) ile olası (probabilistic) yaklaşımlar, kolokasyon adında bütünleşerek jeodezide eş ağırlıklı iki
partner olarak uygulanmaya başlamıştır. Her ne kadar kolokasyon
bugün, meslek çevrelerince (eski alışkanlıkların doğal sonucu) genellikle kuramsal yanı ağır basan (soyut) bir yaklaşım olarak değer,
lendirilmekteyse de, çok yakın bir gelecekte pratiğin gereksinimlerine yanıt aranırken başvurulacak (somut) bir yol olduğuna inanılmaktadır. En azından bu satırların yazarının böylesi bir gelişmeden
en küçük bir kuşkusu yoktur.
Jeodezide gözlemler, fiziksel çevrede yoruma yer bırakmayacak
kadar açık seçik bir olgu için yapılmaktadır. Bunun kaynağı gerekir
(deterministie) düşünüştür. Ancak gözlem sonuçları birer istatistik
parametre olarak verilmektedir. Bu da olası düşünüşten kaynaklanmaktadır. Demek ki jeodezinin en küçük faaliyet birimlerinden birisi
olan belirli bir doğal olgunun gözlenmesinde gerekir (deterministie)
ve olası (probabilistic) düşünüşler biribirlerini tamamlayarak bütünleşmektedirler. Burada olası (probalistic) düşünüşe gereksinim, fiziksel çevredeki bir olgunun incelenmesinde araç olarak görev yapan
aletteki, gözlemcideki ve ortamdaki nedeni bilinmeyen ancak sonuçları gözlemlere yansıyan belirsizliklerin (gözlem hataları, çelişkiler)
bilimsel bir yöntemle ortaya konulması zorunluğundan doğmaktadır.
Ölçü ve gözlemlerle ilintili olarak bu olası (probabilistic) düşünüşe gereksinim yargısının, belge tarama, kişilerle görüşme, hesaplama, çizim, karşılaştırma, sınıflandırma, ayırma, birleştirme, süzme,
vb. öteki birim faaliyetlerde ve kütük, kayıt, çizelge, harita, plan,
belge, rapor, matematik fonksiyon, yeryüzü işareti, vb. ürünlerde de
geçerliliği savunulabilir.
Kısacası, bir genel değerlendirme, jeodezinin içeriğinde kuram
(teori) ile kılgının (pratiğin), ayrıştırılamaz bir îçiçeçlikle kenetlenmiş
olduğunu, biribiriyle alabildiğine bütünleşen gerekir (deterministie)
ve olası (probabilistic) düşünce sistemleriyle, sergilemektedir.
5-SO.NUÇ
Girişte kuram (teori) ile kılgıyı (pratiği) bir arada görmek istemeyen, ya da görmemeyi inatçı bir alışkanlık haline getiren çevrelerden söz edilmiştir. Bunların bir bölüğüne göre, kuramsal (teoriye
ilişkin) çalışmalar, yalın bilimsel dürtülerle bilimin evrensel boyutlarına katkılarda bulunmak amacıyla yapılır. Pratik isterse teoriye iliş114
kin çalışmaların bulgularını alır kullanır, öteki bölüğe göre de, nesnelerin ve olayların özüne inmenin pratik açısından hiç bîr anlamı
yoktur, pratikte önemli olan tek şey sonuçtur. Kuramın (teorinin)
kılgıya (pratiğe) bir mesajı varsa, bunu kavramlar, düşünüş sistem»
leri, vb. biçimlerde değil sonucu açık seçik sergileyen örnekler biçiminde söylemelidir. Böylece, biribîrinin zıddı görünümdeki bu bölüklerin koalisyonuna göre kuram (teori) ile kılgının (pratiğin) herhangi
bîr çalışmada içiçeliği söz konusu olamaz. Hatta bu anlayışın yay.
gınhk oranı ve kemikleşmesi öylesine boyutlara ulaşmıştır ki araştırma çalışmalarının önlerine konan temel, uygulamalı, geliştirmeli
vb. sıfatlarla bunlar parsellenme eğilimindedir.
işte bu anlayışla koşullanmış çevrelerin, jeodezinin içeriğine
ilişkin yukarıdaki genel değerlendirmeyi benimsememeleri kadar doğal bir sonuç beklenemez. Nitekim bu durum öğretim planlarına, tüzük, talimat, yönetmelik, vb.'ne kadar yansımıştır. Bu yansımanın
doğal bîr sonucu olarak da, pek çok meslek çalışanı, hatta bunları
düzenleyip kurallar koyanlar bile, kurama (teoriye) ve olası (probabilistic) düşünce sistemine ilişkin kavram ve özleri meslekten dışlayamamakta (çünkü doğasında bunlar bulunmaktadır), ancak bilinçsiz bir davranış ve süregelen alışkanlıklarla kılgıya (pratiğe) ve gerekir (deterministle) düşünceye ilişkin zorlama bir mantıkla yorumlayıp
uygulamaktadır. En çarpıcı örneklerden birisi, yönetmeliklerdeki hata
sınırının (tecvizin), kendisinin düediğince kullanabileceği bîr hak
olduğuna inanan anlayıştır.
Bununla beraber, bazı örnekleri aşağıda sunulan kaynaklar, bu
kısır döngüden çıkış arayışlarının bilincinin doğmaya başladığının
bir kanıtıdır. Bu uyanışın hızlandırılması, toplum ahlâkının, meslek
ahlâkının ve hatta bilim ahlâkının bir gereğidir. Bunlan özümsemiş
meslek çevrelerine düşen görev, başta öğretim planlan olmak üzere
ülkemizde uygulamaları düzenleyen ve kurallar getiren tüzük, talimat, yönetmelik vb. ile kurum organizasyonlarının yeniden gözden
geçirilerek, bunlarda, gerekir (deterministle) ve olası (probalistic)
düşüncelerin oluşturduğu bütünlük içinden, kuram (teori) ile kılgıya
(pratiğe) BİRLİK İLE BAKILMASI'nı gerçekleştirme çabasına girmektir.
Gelişmekte olan bir toplum niteliğindeki Türkiye gerçeğinde,
kuram (teori) ile kılgıya (pratiğe) BİRLİK İLE BAKILMASI'na en büyük gereksinim, yapılan inceleme, çözümleme, araştırma, deneme,
115
vb. çalışmalarda bulunmaktadır. Gerçekten, Türkiye gibi gelişmekte
olan toplumlarda yalnızca bilimin evrensel boyutlarına katkılarda
bulunmayı amaçlayan yalın kuramsal (teoriye ilişkin) çalışmalar hem
gereksinimler açısından anlamsızdır, hem de olanaklar düşünüldüğünde gelişmiş toplumlardakilerle boy ölçüşme şansı yoktur. O toplumlarda gereksinimleri karşılama ile bilimin evrensel boyutlarına
katkılarda bulunma amaçlan üstüste çakışmaktadır. Öte yandan,
Türkiye gibi çağdaş uygarlık düzeyine erişme yarışına soyunmuş gelişmekte olan bir toplumda pratiğin sıçramalarla ilerleyebilmesi, ancak teorinin desteğiyle mümkündür, tersini iyi niyetli yorumlarla savunmak hemen hemen olanaksızdır.
Durum jeodezi mesleği açısından ele alındığında değişen bir şeyin olmadığı, tersine bu görüşün pekiştiği görülmüştür. Öyleyse,
jeodezide her kademeden meslek işgöreninde bu bilincin mutlaka
yaratılması gerekmektedir.
K A Y
N A K Ç A
|"1"| — BAYET, A. Bilim Ahlakı (La morale de la Science), 1982.
[2"| — GRAFAREND, E. Optimierung geodâtischer Messoperationen. 1979.
[3]---GÜRKAN, O. KTÜ Jeodezi ve Fotogrametri BölümüJvIMLS sınıfı
ders notlarından «Jeodezinin Problemleri» (Yayımlanmamıştır),
1980.
[4]—GÜRKAN, O. - E. KOÇAK - H. ÖZEN Jeodezide Lisans Düzeyinde
Öğretim Planlarının Hazırlanmasında Uygulanabilir Bir Yöntem
Önerisi, Jeodezi Öğretimi Simpozyumu, KTÜ, Trabzon, 1982. [5]—
KOCH, K.R. Parameterschatzung und Hypothesentests in linearen
Modellen, 1980. |6"]—MIKHAIL, E.M. and F. ACKERMAN
Observations and least
sjquares, 1976.
[7]—MOITZ, H. Least sfluares collocation, 1973. [8]—MORITZ, H. - H.
SUNKEL Approximatîon Methods in Geodesy,
1978.
[9]—MORITZ, H. Advanced physical geodesy, 1980. [10 "|—PAPOULIS,
A. Probability, Random Variables and Stochastic
Processes, 1965. fil]—RAMONOWSKI, M. Random errors in
observations and the influence of mödulation on their distribution. 1979.
[12"|—SARBANOĞLU, H. Üç boyutta astrojeodezik ağ dengelemesi, 1982.
[13] — SPIEGEL, M. R. Theory and problems of Statistics. 1961.
116
TOPYEKUN KIRSAL KALKINMA SORUNLARI
Prof. Dr. Nazmi YİLDİZ
Yıldız Üniversitesi
Özellikle İkinci Dünya Savaşı'ndan sonra hemen tüm ülkelerde
giderek artan bir hızda kentlere göç başlamıştır. Kırsal bölgelerdeki
yaşam zorluğu ve toprak yetersizliğinin ilk sıralarda neden olduğu
kentleşme olgusu, sanayileşme sürecine girememiş ülkeleri hazırlıksız yakalamış, kentlerin çevreleri sefalet mahalleleri ve gecekondularla dolmuştur.
Kentlere olan kırsal nüfus akınının kanalize edilerek yavaşlatılması için tarımsal alanlara hizmet götürme fikri, topyekûn kırsal
kalkınma sorunlarını ön plana çıkarmıştır. Bu amaçla, sanayileşmiş
ülkelerde çeşitli deneyim ve uygulamalara geçilmiş ve sevindirici
sonuçlar alınmıştır.
Ülkemizde topyekûn kırsal kalkınma konusu uzun süre konuşulmuş, şümullü kalkınma, il düzeyinde kalkınma, İsrail örneği kalkınma modelleri üzerinde durulmuş, politikacılar uzun zaman «Kentte
ne varsa köyde de olacaktır!» gibi iddialı deyimler kullanmışlardır.
Bu arada topyekûn kırsal kalkınma sorunlarının merkezköy ya da
köy-kent planlama ve uygulaması ile çözüme kavuşturabileeeği ileri
sürülmüş, birara köy-kent uygulamasına bile başlanmıştır.
Topyekûn kırsal kalkınma sorunları ile ilgili olarak ülkemizde
somut bir fikir birliği sağlanamazken Orta ve Batı Avrupa ülkelerinde, özellikle Federal Almanya, Fransa, Hollanda, İsviçre, Belçika ve
Avusturya'da bu konuda yapılan uygulamalar çok başarılı olmuştur.
Anılan ülkelerde sürdürülen çalışmalar havza birimi esasına dayanmakta, 10 bin hektara (100 km2) kadar olan proje alanları yeniden
düzenlenmekte, bu birimler içine bir kaç belde ve bir çok köy girmektedir. Yeniden düzenlenen alanlarda kır-kent ayrımını ortadan
kaldıracak yönde akla gelebilen her hizmet gözönünde tutularak
gerçekleştirilmekte, bu arada büyük bayındırlık projeleri uygulanmaktadır.
Topyekûn kırsal kalkınma projeleri genellikle kırsal alanları, diğer deyimle, tarımsal bölgeleri içine aldığından çiftçileri çok yakından ilgilendirmekte, onların işletmelerini büyük ölçüde iyileştirerek
117
dağınık parsellerinin biraraya getirilmesini (toplulaştırılmasını) sağlamaktadır. Bu nedenle topyekûn kırsal kalkınma çalışmaları tarım
reformunun çekirdeğini oluşturan «Arazi Toplulaştırması» bazına dayanmakta, yol ve sulama ağına bağlanarak toplulaştırman işletmelerin verimleri birkaç kat artmaktadır. Böylece, Arazi Toplulaştırması'
deyimi Yeniden Kırsal Düzenleme ya da Topyekûn Kırsal Kalkınma
anlamına kullanılmaktadır.
Topyekûn kırsal kalkınma projelerinde, aynı zamanda büyük ölçüde toprağa gereksinim duyulan bayındırlık planlarının uygulanma,
sı da sağlanmakta, pratik ve yasal bir yöntemle gerekli araziler proje bölgesi içindeki işletmelerden eşit orantıda kesilmektedir. Böylece sosyal adalet yerine getirildiği gibi hiç bir çiftçinin toprağından
kopmaması da gerçekleştirilebilmektedir. Topyekûn kırsal kalkınma
sorunlarında toprak edinilmesi yolu ilk planda önemli bir sorun olarak karşımıza çıkmaktadır.
Ülkemizin kalkınmasında çeşitli büyük projelerin uygulanmasının
özel bir anlamı vardır. Gerçekleştirilmesi gereken projelerin gereksindiği yerleri kolayca sağlamak başarının göstergelerinden biridir.
Kara ve demiryolları, sulama işleri ve barajlar, hava limanları, millî
savunma tatbikatı yapılacak bölgeler, iskân, sanayi ve turizm projeleri, yeni kurulacak köyler gibi yatırımlar büyük çapta araziyi gerektirmekte, bu amaçla sürdürülen toprak edinme işleri ayrı kuruluşların yetki ve sorumluluğunda bulunmaktadır.
Genel olarak arazi sağlanması için Türkiye'de en geçerli yol
kamulaştırmadır. Oysa kamulaştırma, aktif toprak politikası içinde
taşınmaz edinilmesinde uygulanacak en son yöntemdir. Son ültimatom (Ultima Ratio) olan kamulaştırma, mülkiyeti ortadan kaldırıcı
niteliği nedeniyle en uzun süreli ve en pahalı bir yöntemdir. Aktif bir
toprak politikasında kamulaştırma en sonda yer alır. Kamulaştırmadan önce izlenen sistem şöyledir :
a) Toprak sahibi ile anlaşma yoluna gidilir ve gerekli parseller
normal olım-satım bedeli ile edinilir.
b) Anlaşma sağlanamazsa trampa yoluna başvurulur. Toprak
sahibine başka bir yerde arazi verilir ve gereksinilen parsel ile ara
sındaki bedel farkı para ile denkleştirilir.
c) Öncelikli satmalına (şuf'a) hakkından yararlanılır. Bu hak
tan yararlanan kamu kuruluşu, araya girerek A'nın B'ye sattığı ara118