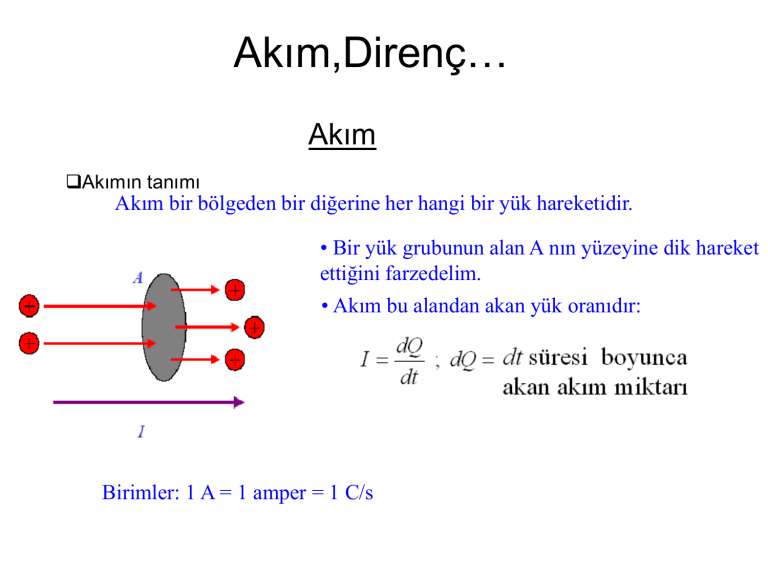
Akım,Direnç…
Akım
Akımın tanımı
Akım bir bölgeden bir diğerine her hangi bir yük hareketidir.
• Bir yük grubunun alan A nın yüzeyine dik hareket
ettiğini farzedelim.
• Akım bu alandan akan yük oranıdır:
Birimler: 1 A = 1 amper = 1 C/s
Akım
Akımın
mikroskobik görünüşü
Akım
Akımın
mikroskobik görünüşü
Akım
Akımın
mikroskobik görünüşü
• Dt zamanında elektronların hareket ettikleri mesafe
Dx d Dt
•q yükünü taşıyan birim hacimde n tane parçacık vardır.
• Dt zamanda A alanını geçen parçacık miktarı:
DQ q(nAd Dt )
• I akımı ifadesi:
dQ
DQ
I
lim
nq d A
D
t
0
dt
Dt
• J akım yoğunluğu ifadesi:
I
J nq d
A
J nqd
Birim alandaki akım
birimleri: A/m2
Akım yoğunluğu vektörü
Özdirenç
Ohm
Kanunu
• İletken içerisindeki J akım yoğunluğu, E elektrik alanına ve maddenin
özelliklerine bağlıdır.
• Bu bağlılık genelde komplekstir fakat bazı maddeler için, özellikle
metaller için, J , E ile orantılıdır.
E J
Ohm kanunu
Özdirenç
Ohm
kanunu
• İletken içerisindeki J akım yoğunluğu E elektrik alanına ve maddenin
özelliklerine bağlıdır.
• Bu bağlılık genelde komplekstir fakat bazı maddeler için, özellikle
metaller için, J , E ile orantılıdır.
E J
V/A ohm
Ohm kanunu
J E
Madde
Gümüş
Bakır
Altın
Çelik
(Wm)
1.47 10 8
1.72 10 8
2.44 10 8
20 10 8
Madde
Grafit
Silikon
Cam
Teflon
(Wm)
3.5 105
2300
1010 1014
1013
Özdirenç
İletkenler, Yarıiletkenler ve Yalıtkanlar
• Metaller gibi iyi elektriksel iletkenler genellikle iyi ısısal iletkenlerdir de.
• Bir metalde elektriksel iletimdeki yükleri taşıyan serbest elektronlar aynı
zamanda ısı iletiminin başlıca mekanizmasını oluştururlar.
• Plastik maddeler gibi zayıf elektriksel iletkenler genelde zayıf termal
iletkenlerdir de.
• Yarıiletkenler metallerle yalıtkanlar arasında ara bir değerde özdirence sahiptir.
• Tamamen ohm kanununa uyan bir madde Omik yada lineer madde olarak
adlandırılır.
Özdirenç
Özdirenç
ve sıcaklık
• Bir metalik iletkenin özdirenci hemen hemen her zaman artan sıcaklıkla artar.
(T ) 0 [1 (T T0 )]
Özdirencin sıcaklık katsayısı
Madde
(oC)-1
Alüminyum 0.0039
Prinç
0.0020
0.0005
Grafit
0.00393
Bakır
Referans sıcaklık. (sıkça 0 oC)
Madde
Demir
Kurşun
Manganin
Gümüş
(oC)-1
0.0050
0.0043
0.00000
0.0038
Özdirenç
Özdirencin sıcaklıkla değişimi
• Grafitin özdirenci sıcaklıkla azalır, bu nedenle daha yüksek sıcaklıklarda
çoğu elektron atomlardan bağımsız hale gelir ve daha fazla mobiliteye
sahip olur.
•Grafitin bu davranışı yarıiletkenler için de doğrudur.
•Çeşitli metalik alaşımlar ve oksitler içeren,bazı maddeler Süperiletkenlik olarak
adlandırılan özelliğe sahiptirler. Süperiletkenlik başlangıçta azalan sıcaklıkla
düzgün bir şekilde özdirencin azaldığı ve daha sonra belirli bir Tc kritik
sıcaklığında direncin aniden sıfıra düştüğü bir olaydır.
T
T
Metal
Yarıiletken
T
Tc
Süperiletken
Direnç
Direnç
•ρ özdirencine sahip bir iletken
için,bir noktadaki J akım yoğunluğu olan bir
noktadaki elektrik alan E : E J
• Ohm kanununa uyulduğu zaman, sabittir elektrik alan büyüklüğünden
bağımsızdır.
• Düzgün A kesit alanlı ve L uzunluklu bir teli düşünelim, ve iletkenin uçlarında
yüksek potansiyel ve düşük potansiyel arasındaki potansiyel fark V olsun bu
yüzden V pozitiftir.
E
I
A
J
L
I JA, V EL
E J
V
R
I
Direnç
1 V/A=1W
V
I
L
E V
I
L
A
A
• Potansiyel farktan dolayı akım akışı olduğu için, bir elektriksel potansiyel
kaybedilir; bu enerji, çarpışma sırasında iletken maddenin iyonlarına transfer
edilir.
Direnç
Direnç
• Bir maddenin özdirenci sıcaklıkla değiştiği için,bir spesifik iletkenin direncide
sıcaklıkla değişir. Çok büyük olmayan sıcaklık aralıkları için, bu değişiklik
yaklaşık olarak lineer ilişkiye dönüşür :
R(T ) R0 [1 (T T0 )]
• Direncin spesifik değerlerine sahip olarak yapılan bir devre cihazı direnç
olarak adlandırılır.
I
I
V
Ohm kanunlarına uyan direnç
V
Yarıiletken diyot
Direnç
Örnek : Direncin hesaplanması
b
a
•İç ve dış yarıçapı a ve b olan ,L uzunluğuna sahip,
özdirençli maddeden yapılmış içi boş bir silindir
düşünelim. İç ve dış yüzeyi arasında bir potansiyel
fark oluşturulduğunda akım silindir boyunca radyal
olarak akar.
.
• Şimdi r yarıçaplı, L uzunluklu, dr kalınlıklı silindirik
bir kabuk hayal edelim.
r
A
b dr
b
R dR
ln
2L a r 2L a
Elektromotor kuvveti (emk) ve devre
Tam
devre ve sabit akım
•Bir iletkenin sabit bir akıma sahip olması için, kapalı bir ilmek yada tam devre
formunda olan bir yol parçası olmalıdır.
+
+
++
+
+
E1
E1
E1
+
+
E2
E2
- I
I
I
J
J
J
-
Elektromotor kuvveti (Emk) ve Devre
Devam eden sabit bir akım ve elektromotor kuvveti
•Bir q yükü tam bir devreyi dolaşırken ve başladığı noktaya geri dönerken,
potansiyel enerji başlangıçtaki ile aynı kalmak zorundadır.
• Fakat yük iletkenin direncinden dolayı bir kısım potansiyel enerjisini kaybeder.
• Devrede potansiyel enerjiyi arttıran bir şeye ihtiyaç vardır.
• Potansiyel enerjiyi arttıran bu şey elektromotor kuvveti olarak adlandırılır.
(emk). Birimi : 1 V = 1 J/C
• Emk (E) düşükten , yüksek potansiyele akım akışı sağlar. Emk üreten cihaz emk
kaynağı olarak adlandırılır.
Emk kaynağı
-Şayet q pozitif yükü kaynak içinde b den a ya hareket
b Fe
-
E
a
E +
Fn
Akım akışı
E
ederse, elektrostatik olmayan Fn kuvveti yük üzerinde
Wn=qE pozitif işini yapar.
-Bu yer değişimi Fe elektrostatik kuvvetine zıttır,
bu nedenle yükle birlikte potansiyel enerji qVab
den dolayı artar.
- İdeal bir emk kaynağı için Fe=Fn aynı büyüklükte
fakat zıt yöndedir.
-Wn=qE=qVab, so Vab=E=IR ideal kaynak için.
Elektromotor kuvveti (emk) ve devre
İç
direnç
• Devredeki gerçek kaynak ideal olarak davranmaz; devrede gerçek bir kaynağa
karşı potansiyel fark emk ye eşit değildir.
Vab=E – Ir (Terminal voltaj, r iç dirençli kaynak)
•Bu yüzden sadece I=0 iken Vab=E doğrudur. Bununla birlikte,
E –Ir = IR yada I = E / (R + r)
Elektromotor kuvveti (emk) ve devre
Gerçek
batarya
cc
I
a
b
r
dd
R
Battery
+
b
a
−
•Gerçek batarya r iç direncine sahiptir .
• Terminal voltajı, ΔVverim = (Va −Vb) = − I r.
•
DVout
I r
I
R
R
I
Rr
Elektromotor kuvveti (emk) ve devre
İdeal
direnç devresindeki potansiyel
c
d
a
b a
b
c
d
b
Elektromotor kuvveti (emk) ve devre
Gerçek
şartlardaki direnç devresinin potansiyeli
c
I
d
R
Battery
r
a
b
-
+
V
ba
r
R
+
-
Ir
IR
0
d
c
ab
ab
Elektromotor kuvveti (emk) ve devre
Örnek
r 2 W, 12 V, R 4 W
A
a
Vcd Vab
b
V
ampermetre
I
Rr
Vab Vcd .
12 V
2 A.
4W2W
Vcd IR ( 2 A)(4 W) 8 V.
Vab Ir 12 V - (2 A)(2 W) 8 V.
voltmetre
The rate of energy conversion in the battery is I (12 V)(2 A) 24 W.
The rate of dissipatio n of energy in the battery is Ir 2 (2 A) 2 (2 W) 8 W.
The electrical power output is I I 2 r 16 W.
The power output is also given by Vbc I (8 V)(2 A) 16 W.
It is also given by IR 2 (2 A) 2 (4 W) 16 W.
Elektrik devresindeki enerji ve güç
Elektrik
Gücü
Elektriksel devre elemanları elektriksel enerjiyi
1) Isı enerjisine( dirençteki gibi) yada
2) Işığa (ışık yayan diyottaki gibi) yada
3) İşe (bir elektrik motordaki gibi) dönüştürür.Bu, kaynak
sağlanan elektriksel gücü bilmek için yararlıdır.
Vab
Şekildeki basit devreyi düşünelim .
dU e dQDV dQVab
dQ dirence karşı hareket eder ve potansiyel
R
ΔV den V ye düşer bu yüzden dUe elektrik
potansiyel enerjisi kaybedilir.
Elektriksel güç= Ue den sağlanan oran.
Vab
Elektrik devresindeki enerji ve güç
Bir
kaynağın güç verimi
• r iç dirençli bir emk kaynağının bir dış devreye ideal bir iletkenle bağlandığını
düşünelim.
• Dış devreye verilen enerji oranı aşağıdaki gibi verilir:
P Vab I
•Bir emk E ve bir r iç direnci ile tanımlanan bir kaynak için:
Vab Ir
Kaynağın
net elektriksel
güç verimi
+
batarya
P Vab I I I r
Kaynakta elektriksel
olmayan enerjinin
elektriksel enerjiye
dönüşüm oranı
2
Kaynağın iç
direncinde yitirilen
elektriksel enerji
oranı
-
(kaynak)
I
a+
Projektör
(Dış devre )
b-
I
Elektrik devresindeki enerji ve güç
Bir
kaynağın güç girişi
r iç dirençli bir emk kaynağının bir dış devreye ideal bir iletkenle bağlandığını
Bataryaya toplam elektriksel
düşünelim.
güç girişi
+
Vab Ir P Vab I I I 2 r
battery
small emf
I
a+
Fn
v
+
b-
I
Bataryada elektriksel
enerjinin elektriksel
olmayan enerjiye
dönüşüm oranı
Büyük emk dönüştürücü
Bataryada iç
dirençteki enerji
yitim oranı
Elektrik iletimi
Drude
modeli
Elektrik iletimi
Drude
modeli
Elektrik iletimi
Drude
modeli