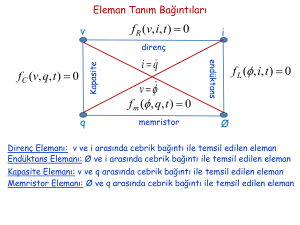
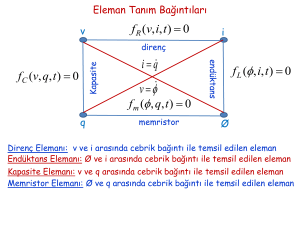
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
ONBİRİNCİ BÖLÜM: BOBİNLER
Anahtar Kelimeler
Faraday kanunu, Lenz kanunu, henri, joule, endüktans, özendüktans, L, L/R zaman sabiti,
Elektrik ve elektronik devrelerde bilinmesinde fayda olan bir diğer önemli kavram endüktanstır.
Sargılar (bobin) elektrik enerjisini geçici olarak depolayabilmektedir. Özellikle ayar ve filtre elemanı
olarak geniş bir alanda kullanılmaktadır. Ayrıca transformatörlerde ateşleme devrelerinde sıklıkla
karşımıza çıkmaktadır. Bu bölümde bobin ve endüktansının doğru akım devrelerinde hangi etkilerde
bulunduğu üzerinde durulacaktır.
Bu bölümde kazandırılacak yeterliklerden sonra öğrenci;
Endüktans ve özendüktansı tanımlar.
Faraday ve Lenz kanunlarını açıklar.
Belirtilen devre şartlarında endüklenen gerilimi hesaplar.
Verilenlerden faydalanılarak endüktansı hesaplar.
Seri ve paralel endüktansların eşdeğeri bulur.
Manyetik alanda depolanan enerjiyi belirler.
Zaman sabiti çizgilerini çizer ve açıklar.
Verilen devre şartlarında zaman sabitlerini hesaplar.
RL devrelerinin doğru akımda nasıl çalıştığını öğrenir.
TEMEL BİLGİLER
Dirençler akım akışına karşı koyan devre elemanlarıdır. Endüktanslar ise akımdaki değişime karşı
koyan elemanlardır.
Aşağıdaki şekilde görüldüğü gibi fiziki ve elektriki olarak çok değişik bobinler vardır. Bu şekilde
gördüğünüz bobinler akımdaki değişime karşı koymak üzere tasarlanmışlardır. Belirtmemiz gerekir ki,
düz bir kablo parçası da ufak bir miktar endüktans gösterir. Çoğu durumda bu istenmeyen endüktans
devre tasarımında dikkate alınmalıdır. Özellikle yüksek frekans devrelerinde bu nokta kesinlikle göz
ardı edilmemelidir. Altını çizerek bir kez daha vurgulayalım ki, endüktans akım akışına değil, akımdaki
değişime karşı koyuştur.
Bir diğer önemli endüktans karakteristiği bobinlerin manyetik alan içinde elektrik enerjisi
depolayabilmeleridir. Bobinden geçen akım arttıkça oluşan manyetik alan bobini çevreleyerek genişler.
Akım azaltılmaya çalışıldığında genişleyen alan daralır ve akımdaki azalışı engellemeye çalışır. Alan
genişledikçe enerji soğurur ve depolar. Alan daraldığında depoladığı enerjiyi devreye geri verir.
Endüktans ve bobinin bir diğer önemli özelliği içlerinden geçen akım değiştiğinde bir e-m-k
üretmeleridir. Bu üretilen e-m-k’ nın sebebi genişleyen veya daralan manyetik alanın sargı iletkenlerini
kesmesidir. Kendi kendine üretilen bu e-m-k ya bazen zıt e-m-k da denir. Çünkü kutuplanması kendini
üreten değişime karşı koymaktadır. Endüktansların bahsedilen durumu oluşturması konusuna işaret
etmek üzere özendüktans kavramı sıklıkla kullanılmaktadır.
Manyetizmanın anlatıldığı bölümde bobinler ve manyetik alanla ilişkileri konusu ayrıntılı olarak ifade
edilmiştir. Orada anlatılanlarla endüktansı özelliğin arasındaki ilişkiler bu bölümde ele alınacaktır.
Elektromanyetizmayı anlatırken sabit değerli doğru akım geçirerek sargının davranışını incelemiştik.
Bu bölümde ek olarak anahtarın açıldığı ve kapatıldığı kısa sürelerde geçici durum çalışma şartlarını
irdeleyeceğiz. Yani endüktans içeren bir devreye doğru akımın uygulandığı ve kesildiği anlarda
gerçekleşen olayları mercek altına alacağız.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 11.1. Değişik bobinler ve simgeleri
Şekil 11.2. Genişleyen ve daralan alanlar
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 11.3. Zıt e-m-k kavramı
Endüktans konusunun daha iyi anlaşılabilmesi için manyetizma konusunda ayrıntıları ile anlatılan
Faraday ve Lenz kanunlarının kısaca özetlenmesinde fayda vardır.
Faraday Kanunu
Bir devrede indüklenen e-m-k devredeki manyetik akı değişiminin zaman değişimine oranıdır. Bir diğer
ifade ile indüklenen e-m-k nın miktarı kesen akıların oranına bağlıdır. SI birim sisteminde bir Weber
108 akı çizgisine eşittir. Oluşan gerilimin değerini belirleyen denklem şudur:
VİND=dØ / dt
Burada dØ / dt akı çizgilerinin kesme hızı veya oranıdır. Akı çizgileri tarafından kesilen sadece bir
iletken değil de bir sargı olduğunda ve sargının sarım sayısı N ise, VİND=N.dØ / dt olur.
Mesela 500 sarımlı bir sargı saniyede 2 Weberlik akı değişim hızı ile kesiliyorsa bu sargıda
VİND=500.2 / 1=1000V gerilim indüklenecektir.
Lenz Kanunu
İndüklenen gerilim veya akımın yönü kendini oluşturanın değişimine karşı koyar. Yani bir elektrik
devresinde varolan manyetik akı değişimi ile indüklenen e-m-k (ve bu e-m-k nın oluşturduğu akım)
kendilerini oluşturan bu akı değişimine karşı koymaktadır.
Özetle faraday kanunu ilgili parametreler tarafından üretilen gerilimin miktarını ve Lenz kanunu da
üretilen bu gerilim ve akımın kutuplanmasını ve doğasını tanımlamaktadır.
Bu kısa hatırlatmalardan sonra endüktansın doğru akım karakteristiklerini anlatabiliriz.
ÖZENDÜKTANS
Endüktansı akımdaki değişime karşı koyan bir devre özelliği olarak tanımlamıştık. Özendüktans
devreden akan akım değiştiğinde bir gerilimin üretilmesi anlamında bir elektrik devre özelliğidir.
Endüktans L simgesi ile gösterilir ve birimi Henridir. Henri kısaca H olarak yazılır.
Tahmin edebileceğiniz gibi üretilen e-m-k nın genliği veya miktarı endüktansın değeri ile akımdaki
değişim oranı veya hızına bağlı olacaktır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
VL=L di / dt
Burada di, amper cinsinden akımdaki değişim, dt saniye cinsinden zamanda değişim ve dolayısıyla di /
dt amper/saniye cinsinden akımdaki değişim hızıdır.
Burada dikkat edilmesi gereken önemli bir unsur şudur: Sargıdan geçen akımın oluşturduğu gerilim
kaynak gerilimine karşı koyacak şekilde kutuplanmaktadır.
Yukarıda anlatılanlardan şu sonucu çıkarabiliriz. İçinden geçen akım değişimi saniyede 1A olan bir
devrede bu olay yüzünden 1V gerilim indükleniyorsa o devrenin endüktansı 1Henridir. İndüklenen bu
gerilimin kaynak gerilimine göre karşı yönde olması yüzünden zıt e-m-k adı kullanılmaktadır.
Örnek
10H’lik bir sargıda saniyede değişim hızı 5A olan bir akım geçiyorsa sargıda üretilen e-m-k nın
genliğini hesaplayalım.
Çözüm
VL = L di/dt = 10.5 = 50V
ENDÜKTANSI BELİRLEYEN ETKENLER
Hatırlayacağınız gibi bir sargının elektromanyetik alanının gücünü belirleyen etkenler sargının
endüktans değeri ile de ilgilidir.
Şekil 11.4. Endüktans miktarını etkileyen etkenler
Bobinlerin endüktans değerini etkileyen fiziksel özellikleri şunlardır:
1) Sarım sayısı : Sarım sayısı arttıkça endüktans değeri de artar. Daha doğru bir ifade ile
endüktans sarım sayısının karesi ile orantılıdır. Yani belirli bir uzunluk ve çapa sahip bir
bobinin sarım sayısı iki katına çıkarılırsa çekirdek malzeme aynı kalmak şartıyla endüktans
değeri dört katına çıkar.
2) Sargının kesit alanı : kesit alanı ile endüktans değeri doğru orantılıdır. Yani kesit alanı iki
katına çıkartılırsa endüktans da iki katına çıkar.
3) Sargının boyu : Belirli bir çap ve sarım sayısı için sargı boyu arttırılırsa endüktans değeri
düşer. Bunun sebebi sargı uzunluğunun arttırılması ile birim zamanda daha az akı tarafından
sargı iletkenlerinin kesilmesi ve daha az gerilimin üretilmesidir.
4) Çekirdeğin bağıl manyetik geçirgenliği : Hava çekirdekli sargılar için bağıl manyetik geçirgenlik
r=1’dir. Sargının çekirdek malzemesinin bağıl manyetik geçirgenliği büyük olursa endüktans
değeri de büyür. Bildiğiniz gibi manyetik geçirgenlik manyetik akı çizgilerini yoğunlaştırarak
manyetik yolun bu anlamda yeteneğini arttıran bir özelliktir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Bir sargı tasarlanmak istenirse SI birim sistemi kullanılarak aşağıdaki denklemden faydalanılabilir:
L = 12,57. 10-7 . r . N2 . A / l
Burada L henri cinsinden endüktans, r bağıl manyetik geçirgenlik, N sarım sayısı, A metrekare
cinsinden kesit alanı, l metre cinsinden sargı boyu, 12,57.10-7 havanın mutlak manyetik geçirgenliğidir.
Örnek
Hava çekirdekli bir sargının boyu 0,01m, kesit alanı 0,001m 2 ve sarım sayısı 2000 ise endüktansı
nedir?
Çözüm
L=12,57. 10-7 . (1.20002 . 0,001 / 0,01)=0,5H=500mH
ENDÜKTANSLARIN SERİ VE PARALEL BAĞLANMASI
Bu kısımda sargılar arasında kuplaj olmadığını varsayacağız. Yani bobinlerin herhangi birinin akı
çizgilerinin diğer bir bobini etkilemediğini düşüneceğiz. Bir başka ifade ile sargılar arasında karşılıklı
veya ortak endüktansın olmadığını varsayacağız.
Seri bağlı endüktanslar
Şekil 11.5. Endüktansların seri eşdeğeri
Seri bağlı endüktansların eşdeğeri seri bağlı dirençlerdeki gibidir. Yani n tane endüktans seri bağlı ise
bunların eşdeğeri:
LT=L1+L2+L3+......Ln
Ancak bu denklemin bobinler arasında kuplaj olmadığı durumlarda geçerli olduğu aksi durumda
kullanılamayacağı unutulmamalıdır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Paralel bağlı endüktanslar
Paralel bağlı endüktansların eşdeğeri en küçük paralel endüktanstan daha küçük olacaktır. Yani
paralel bağlamada durum dirençlerde olduğu gibidir.
Şekil 11.6. Paralel bağlı endüktansların eşdeğerinin bulunması
Şekil 11.7. Paralel bağlı endüktansların eşdeğerinin bulunması
SARGININ MANYETİK ALANINDA DEPO EDİLEN ENERJİ
Sargı içinden bir akım geçtiğinde sargı etrafında oluşan manyetik alan depolanan enerji şeklindedir.
Elektromanyetik alanı üreten akım devrenin kaynağı tarafından sağlanmaktadır. Bu nedenle
depolanan bu enerji manyetik alan kaynaktan sağlanmaktadır.
Kaynak devreden alındığında depo edilen enerji alanın daralması ile birlikte indüklenen e-m-k şeklinde
devreye geri döner. Bu e-m-k, sargıdan akan ve azalmakta olan akımı korumaya çalışır.
Eğer sargı mükemmelse yani direnci yoksa I2.R kayıpları oluşmaz. Bu durumda enerjinin depolanması
ve tekrar devreye geri verilmesi süreçlerinde güç harcanmaz. Ancak gerçekte kullanılan iletken
yüzünden sargıların bir miktar dirençleri vardır ve az da olsa güç harcarlar. Sargıların bu omik direnci
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
hesaba katılacak kadar önemli ise endüktansı ile seri bağlı olduğu kabul edilerek ohm kanununa göre
dikkate alınır.
Şekil 11.8. Sargının manyetik alanında enerjinin depo edilmesi kavramı
Şekil 11.9. Sargıdan geçen doğru akımın değerinin ohm kanunu ile bulunması
Yukarıdaki şekilde omik direnci 10 olan bir sargıya 20V2luk doğru gerilim uygulanmıştır. Sargı
etrafındaki alan oluştuktan sonra sargıdan akan doğru akımın değeri 2A olacaktır.
Elektrik enerjisinin biriminin Joule olduğunu daha önce söylemiştik. 1Joule aralarındaki potansiyel fark
1V olan iki nokta arasında 1Kulonluk elektrik yükünü taşımak için gereken elektrik enerjisi miktarıdır.
Yine hatırlayacağınız gibi 1W’lık güç saniyede 1Joule’lük elektrik işinin yapılmasına denk düşmektedir.
Bütün bunlardan sonra sargıda depo edilen enerji sargıdan geçen akım ve sargının endüktans değeri
ile ilgili olacaktır. Yani;
W=(1/2).L.I2
Burada W Joule cinsinden enerji, L Henri cinsinden endüktans, I amper cinsinden akım şiddetidir.
Örnek
Endüktansı 20H olan bir sargıdan 5A geçiyorsa sargının depoladığı enerji ne olur?
Çözüm
W=(1/2).20.52 =250Joule
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
L/R ZAMAN SABİTİ
Daha önce söylediğimiz gibi sargılar sarımlarını kesen manyetik alanın genişlemesi ve daralması
yüzünden içlerinden geçen akımın değişmelerine karşı koyarlar. İndüklenen gerilim kendi kendini
oluşturan sebebin değişimine karşı koymaktadır (Lenz kanunu). Buna göre sargıya doğru gerilim ilk
uygulandığında sargıdan geçen akım en büyük değerine hemen ulaşamaz.
Doğru gerilim ilk uygulandığında basit bir endüktanslı devrede devre şartlarının ani değişimi geçici bir
çalışma durumuna yol açar.
Şekil 11.10. Saf omik bir devrede doğru akım değişimi
Şekil 11.11. Endüktanslı bir devrede doğru akım değişimi
Yukarıdaki iki şekle göre aşağıdaki açıklamalar yapılabilir:
1) İlk devreye baktığımızda bir doğru akım kaynağı bir doğru gerilim kaynağı ve saf omik bir
direnç görmekteyiz. Anahtar açıkken sıfır olan devre akımı anahtar kapatılır kapatılmaz ohm
kanunu ile belirlenen değerine ulaşmakta ve o değerde kalmaktadır.
2) İkinci devrede hem endüktans, hem de omik yük vardır. Devre şeklinin yanında verilen akım
değişim eğrisinden görülebileceği gibi anahtar kapatılır kapatılmaz devre akımı sıfırdan normal
değerine çıkamamıştır. Bunun sebebi anahtar kapatıldıktan sonra sargıdaki manyetik alanın
genişlemeye başlamasıdır. Genişleyen bu alan sargının sarımlarını keser. Bir ters e-m-k
oluşturur ve bu ters e-m-k akımdaki değişime karşı koyar. Sonuç olarak anahtar kapatıldığında
devre akımının normal değerine erişmesi hemen mümkün olmaz. Eğriye bakmaya devam
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
edersek t1 zamanında akımın son değerinin %63,2’sine eriştiğini ve t0’dan t1’e kadar olan
zamanı L / R’ ye eşit olduğunu görebiliriz. L / R değeri zaman sabiti olarak bilinir ve simgesi
ile gösterilir.
=L/R
Denklemden görüldüğü gibi zaman sabiti henri cinsinden L endüktansı ile doğru orantılı iken ohm
cinsinden R direnci ile ters orantılıdır.
Belli bir akım değişimi için endüktans değeri büyütüldükçe üretilen zıt e-m-k da büyümektedir. Yani L
değeri büyüdükçe akım değişimine karşı koyma işi de büyümektedir. Bunun anlamı akı ve akımın en
büyük değerine ulaşması için (sürekli durum seviyesi) daha çok zamanın gerekeceğidir. Bu seviyeye 5
zaman sabiti sonrasında ulaşılır. Bir diğer deyişle L arttıkça artar, L azaldıkça azalır.
Ohm kanunundan bildiğimiz gibi I=V / R olduğundan daha küçük direnç değerleri için sabit gerilim
altında daha çok akımlar elde edilir. Bu yüzden yüksek akım değerine ulaşmak için ihtiyaç duyulan
akımdaki değişim miktarı da büyür. Dolayısıyla bir zaman sabiti için geçen süre de artar. Yani R
azaldıkça artar, R arttıkça azalır.
Bütün bunları hafızamızda tutarak yukarıda verilen devre ile zaman sabiti değişim eğrisine tekrar
bakalım. Bu eğriyi genellikle genel zaman sabiti eğrisi denmektedir.
3) t2 zaman anında (t1’den t2’ye kadar olan zaman ikinci zaman sabitini temsil eder) akım en son
doğru akım seviyesine t1 anından itibaren erişmek için kalan miktarın %63,2’sine erişmiştir.
Yani t1 anında erişilen %63,2’lik miktardan sonra tam değere ulaşmak için geri kalan %36,8’lik
miktarın %63,2’sine t2 zaman anında erişilmiştir. %36,8’in %63,2’si olan %23,3 değerini t 1
zaman anında erişilen %63,2’ye eklersek %86,5 değerini elde ederiz ki, bu değer en son
doğru akım seviyesinin t2 zaman anında %86,5’ine erişildiğini göstermektedir.
4) Her zaman sabiti için akımın son değerine ulaşmak için kalan miktarın %63,2’si kadar akım
değeri yükselir. 5 zaman sabiti onunda akım en son değerine ulaşır. Bu anda akımın değeri
5V/5=1A’dir. Böylece akımı en büyük V/R değerine ulaşması için gereken zaman L
endüktansı ile doğru R devre direnci ile ters orantılıdır ve zaman sabitinin L/R’ ye eşit olması
durumunu açıklar.
Sargının genişleyen manyetik alanı ve bunun sonucunda üstel olarak artan akımın ürettiği gerilim saf
omik dirençli devrelerde çok ani gerçekleşen bir olaydır.
Sargı etrafındaki alan tam olarak genişledikten sonra doğru gerilim kaynağı devreden çıkartılırsa, yani
sargının alanı daralırsa ne olur? aşağıdaki devrede anahtar A konumunda iken kaynak ile R L devresi
birbirine bağlıdır. Anahtar B konumuna getirildiğinde kaynakla RL devresi arasındaki bağlantı kesilir.
Bununla beraber RL devresi içinde hala bir akım yolu vardır.
Farz edelim ki, anahtar en az 5 zaman sabiti boyunca A konumundadır ve devre akımı en büyük
seviyesine ulaşmıştır. Bu durumda manyetik alan tam olarak genişlemiş olacaktır. Bu anda anahtar B
konumuna getirilirse genişlemiş alan sargıda bir e-m-k indükleyerek daralır. Bu olay akım değişimini
engellemeye çalışacaktır. Sargının daralan alanı ve indüklenen e-m-k bir kaynak gibi davranacaktır.
Sonuçta alan tam olarak daraldığında akım sıfır değerine ulaşmış olacaktır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 11.12. Akımın en büyük değerinden L/R zaman sabitine bağlı olarak sıfır değerine doğru
düşmesi
Şekil 11.13. Genel zaman sabiti eğrisi
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Akımın azalması sürecinde nelerin olduğu konusunda aşağıdaki yorumlar yapılabilir:
1) Akım ilk zaman sabiti boyunca en büyük değerinden %63,2 değerini kaybetmektedir. Yani en
büyük değerinin %36,8’ine düşmektedir.
2) İkinci zaman sabiti boyunca son değerinin %63,2’sini kaybetmekte yani en büyük değerinin
%13,5’i kadar bir değere gerilemektedir.
3) Bu olay devam eder ve 5L/R zaman sabiti sonunda akım neredeyse sıfır seviyesine düşer.
4) Aynı L/R şartlarında akımın artma ve azalma eğrileri birbirlerinin ayna görüntüleridir.
Özetle seri RL devrelerinde akımın durağan seviyesinden en büyük değerine artması veya azalması 5
zaman sabiti kadar zaman gerektirmektedir. Bu durum akım sıfırdan 1A’e, 1A’den 5A’e, 4A’den 2A’e
gibi bir kararlı durumdan bir diğer yeni duruma artma veya azalma yönünde değiştiğinde de böyledir.
Yani bu değişimin mutlaka sıfır ile en büyük değer arasında gerçekleşmesi gerekmez.
Şekil 11.14. Basit bir doğru akım RL devresi
Yukarıda doğru gerilimle beslenen bir RL devresi görülmektedir. Bu devrede VL ve VR gerilimlerinin
toplamı uygulanan V gerilimine eşit olmalıdır. Bunun anlamı RL devresi üzerinden geçen akım arttıkça
VR’nin artması ve bununla orantılı olarak VR’nin azalması, bu durumun akım sürekli durum değerine
eriştiğinde VR’nin uygulanan V gerilimine ve VR’nin de yaklaşık olarak sıfır Volta eşit olduğu ana kadar
devam etmesidir. Bu dediklerimiz sargının omik direncini sıfır ohm kabul edilmesi durumunda
geçerlidir. Daha sonra akım azaldıkça VR gerilimi de azalacak ve bu işlem akımın sürekli durum en az
değerine ulaşmasına kadar sürecektir. eğrileri belirli zaman sonrasında VR ve VL değerlerinin
belirlenmesi için oldukça kullanışlı yöntemlerdir.
Yukarıdaki devrede anahtar kapatıldıktan sonra VR geriliminin değeri ne olacaktır? Bu soruyu
cevaplamak için 1saniyede kaç tane zaman sabiti olduğunu hesaplamak gerekecektir.
=L / R = 10H / 12 =0,833 saniye
Bu durumda 1 saniye = 1 / 0,833 = 1,2
Eğriye bakarsak 1,2 kadar zaman sonra akımın en büyük değerinin %70’ine ulaştığını görürüz.
Bu yüzden;
VR= 0,7. kaynak gerilimi = 0,7 . 10 = 7V
VL= 10-7=3V
DEVRE PARAMETRELERİNİN HESABINDA “e” NİN KULLANILMASI
Devre parametrelerinin herhangi bir zaman anı için belirlenmesinde oldukça doğru sonuçlar veren bir
diğer hesaplama yolu doğal logaritmayı kullanmaktır. Zaman sabiti çizgilerinde gördüğünüz eğriler
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
üstel eğrilerdir. Doğal logaritma üstel değişimlerle ilgili matematik değerleri anlatır. Doğal logaritmanın
taban sayısı 2,71828 dir ve “e” harfi ile gösterilir.
Şekil 11.15. “e” nin negatif kuvvetleri için eğriler
Yukarıdaki şekilde “e” nin negatif kuvvetlerinin arttırılması ile elde edilen ve kendisi azalmakta olan
eğri görülmektedir. e-1 = 0,3679 , e-2 =0,1353 , e-3 = 0,0498 gibi değerler almaktadır (kırmızı eğri). Mavi
eğri ise bu negatif kuvvetli “e” değerlerinin 1’den çıkartılması ile elde edilen noktaların birleştirilmesi ile
elde edilmiştir. Mesela kırmızı eğrideki e-1 =0,3679 değerine mavi eğride karşı düşen değer
1-0,3679=0,6321’dir.
Devre parametreleri ile eğrinin ilişkisi
Yukarı doğru çıkan eğri 5 zaman sabiti boyunca akımın artışını temsil etmektedir. Akım en büyük
değerine doğru arttıkça RL devresindeki direnç uçlarında düşen gerilim de artacaktır. Azalan eğri
harici gerilim kaynağını devreden çıkartılmasından sonra akımın azalışını sargı alanının daralmasını
temsil etmektedir. Benzer olarak akımın azalması ile aynı oranda direnç üzerindeki gerilim düşümü de
adım adım azalacaktır. Her durumda kaynak gerilimi VR+VL’ ye eşit olacaktır. Eğri boyunca herhangi
bir noktada artan ve azalan eğrilerin o noktaya ilişkin değerlerinin toplamı en son değere denk düşen
%100’ü temsil etmek üzere 1 olacaktır.
L/R zaman sabiti ile “e” nin negatif kuvvetleri arasındaki ilişki
“e” nin negatif kuvvetlerinin arttırılması ile elde edilen yer azalan üstel eğrinin neresinde olduğumuzu
belirler. Bildiğiniz gibi 5L/R zaman sabiti sonrasında devre parametreleri bir kararlı durumdan bir diğer
kararlı duruma değişmektedir. Buradaki önemli ilişki şudur : bu değişim için harcanan zaman kaç tane
zaman sabitine denk düşmektedir.
Eğer değişim için izin verilen zaman 5 ya da daha fazla zaman sabitine denk düşüyorsa:
1) Akım en son değerinde olacaktır. Yani ya en büyük değerine erişecek ya da azalarak sıfıra
düşecektir.
2) Akım artıyorsa VR değeri kaynak gerilimine eşit olacak fakat akım azalıyorsa VR sıfır
olacaktır.
3) VL sıfır olacaktır.
Eğer değişim için izin verilen zaman sadece 1 zaman sabiti kadar ise akım yeni en büyük değerinin
%63,2’sine erişecek veya %36,8’ine düşecektir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Eğer izin verilen zamanın miktarını biliyorsak ya da L/R zaman sabitini hesaplayabiliyorsak değişim
için kaç tane zaman sabitine ihtiyaç duyduğumuzu da biliyoruz demektir. İzin verilen zamanın bir
zaman sabiti için geçecek zamana oranı ile elde edilen sayı, devre parametrelerini hesaplamak için “e”
nin negatif kuvveti olarak kullanılacak sayı olacaktır.
[Zaman sabitlerinin sayısı] = [değişim için izin verilen süre (t)] / [bir L/R zaman sabiti için süre]
=(R / L ).t
Dolayısıyla “e” nin negatif kuvveti olarak (R/L).t kullanılmalıdır.
Elde edilecek denklemde akımın ani değeri bulunacaktır. Akım değeri bulunduktan sonra direnç
üzerindeki gerilim düşümü kolayca bulunabilir. Uygulanan gerilim de biliniyorsa o zaman anı için VL
değeri de kolayca hesaplanabilecektir.
Akımın sıfırdan en son değerine doğru arttırılmakta olduğunu veya mevcut değerinden sıfır değerine
doğru azaldığını farz edersek denklemimiz şu şekilde olacaktır.
Artan akım için i=(VS/R).(1- e-(R/L).t)
Azalan akım için i=(VS/R). e-(R/L).t
Örnek
Aşağıdaki devre için VR ve VL’yi bulunuz.
Çözüm
i=(VS/R).(1- e-(R/L).t)
i=(10V/10K).(1- e-(10K / 10H).1ms)=1mA.(1-e-1)=1mA(1-0,3679)=1mA . 0,6321=0,6321mA
Bu sonucu üstel çizge ile de bulabiliriz. izin verilen değişim süresi bir zaman sabiti kadar olduğunda
akımın sıfır değerinden mümkün en büyük değerinin (VS/R=10V/10K=1mA) %63’üne kadar arttığını
görürüz. Bu durumda;
VR=0,63mA.10K=6,3V
VL=10V-6,3V=3,7V
Şekil 11.16. Anahtar kapatıldıktan 1ms sonra akımın değeri ne olur?
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Örnek
Akım en büyük değerinde iken anahtar A konumundan B konumuna değiştiriliyor. Bu değişiklikten
68s sonra akımın değeri ne olur?
Çözüm
i=(VS/R). e-(R/L).t
i=(6V/2,2K). e-(2,2K/50mH).68s = 2,72mA e-2,992 = 0,136mA
Bu sonuç eğrisi ile uyuşmaktadır. 2,992 zaman sabiti sonrasında akım asıl değerinin %5’i değere
sahiptir. Bu anda VR=0,136mA . 2,2K=0,299V olacaktır.
Şekil 11.17.
Alanın çok hızlı daralması çok yüksek gerilimler oluşturur
Yukarıdaki devrede kaynak geriliminin bağlantısı kesildiğinde düşük dirençli bir akım yolu
olmayacaktır. Anahtarın açık kontakları arasındaki direncin çok yüksek olduğunu farz edelim. Anahtar
açıldığı anda akım yolu üzerindeki toplam direnç sert bir şekilde sonsuz değerine çıkacaktır. R sert bir
şekilde arttığından ve L değeri aynı kaldığından L/R’ ye eşit olan zaman sabiti aynı sertlikte
azalacaktır. Bunun sonucu olarak genişlemiş durumdaki alan aynı şekilde birdenbire daralacaktır.
Böylece çok kısa bir zamanda sargının sarımlarını çok sayıda akı çizgisi kesecek ve sargıda çok
yüksek bir gerilim indüklenecektir. Bu gerilim anahtarın kontakları arasında ark oluşturacak kadar
büyük bir değerde olabilir. Daralan alanın temsil ettiği depolanmış manyetik enerji bu şekilde ark
oluşumu ile harcanmış olacaktır. Özetle bobin içeren bir devreye doğru gerilim ilk uygulandığında akım
en büyük değerine hemen erişemez. Bu gecikmenin sebebi bobinin akımdaki değişime karşı koyma
özelliğidir. Gecikmenin süresi 5 zaman sabiti kadardır. Bir zaman sabiti L/R’ ye eşittir. Aynı şekilde
gerilim kaynağı devreden çıkartıldıktan sonra akım hemen sıfır değerine düşemez. Bunun sebebi de
yine bobinin akımdaki değişime karşı koyması ve daralan alanın akım değişimini engelleyen bir e-m-k
indüklemesidir. Akımın azalması sürecinde alanın çok çabuk daralması sargıda çok yüksek değerli
gerilim indüklenmesine yol açar. Bu yüzden tasarımcılar doğru akım devrelerinde bobinden geçen
akımın aniden kesilmediğine emin olmak isterler. Buna rağmen akım aniden kesilirse istenmeyen
gerilim dalgalanmalarından kaçınmak için önlemler alınır.
İnce tabakalı demir çekirdeğe sahip bobinlerin (güç kaynaklarında ve ses devrelerinde kullanılanlarda
olduğu gibi) endüktans değerleri 1H’den büyüktür. Toz haline getirilmiş demir çekirdekli ve değişken
ferrit çekirdekli bobinlerin endüktansı mH’ler düzeyindedir. Hava çekirdekli bobinlerin endüktansları ise
H’ ler seviyesindedir.
Bobinler doğru akım direncini doğrudan etkileyen değişik sarım sayısı ve kablo boyutunda imal
edilirler.