Bölüm 4: Sayısal İntegral
advertisement

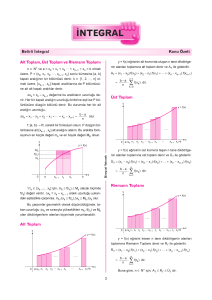
Bölüm 4: Sayısal İntegral Bir f(x) fonksiyonunun tanımlı olduğu bir [a,b] aralığındaki belirli aşağıdaki gibi tanımlanır; b S f ( x)dx a S, [a,b] aralığında f(x) eğrisi ile x-ekseni arasındaki kalan yüzeyin alanıdır. f(x) f(x) a b x Şekil 4.1: Sayısal integral şematik gösterimi f(x) f(b) f(a) a b x Şekil 4.2: Sayısal integralde Trapez yöntemi şematik gösterimi. Şekilde [a,b] aralığında eşit aralıklarla N sayıda nokta belirlersek, adım uzunluğu aşağıdaki gibi olur; (b a) h N a ve b noktalarını da katarak bo noktaları şöyle adlandırabiliriz. x0=a, xi=a+ih, xN=b (i=1,2,3,….,N-1) Şekil 4.2 ‘deki integralin değeri herbir [xi, xi+1] alt aralıklarındaki integral değerlerinin toplamı olacaktır. S x1 x2 xN x0 x1 x N 1 f ( x)dx f ( x)dx ........... f ( x)dx S s1 s2 s3 .......... sN Trapez Kuralı: Trapez kuralı kapalı integral formüllerinin ilki olup, aşağıdaki eşitlikteki polinomun birinci dereceden olduğu duruma karşılık gelir: b b a a I f ( x)dx f1 ( x)dx Şekil 4.5’i dikkate aldığığımızda, eğer h adımı çok küçükse, en basit yaklaşıklıkla, her bir aralıkta fonksiyonu bir doğru parçası olarak alırız. Bu durumda, [xi, xi+1] aralığında oluşan yamuğun alanı hesaplanabilir: si ( f i f i 1 ) h 2 Burada fi sol kenar, fi+1 sağ kenar ve h genişliktir. f(x) f(x) h ......... x0=a x1 x2 x3 . . . . xn=b x Şekil 4.3. N tane yamuk alanı toplanırsa, sayısal integral için trapez formülü bulunmuş olur.(Şekil4.3.) S b a ( f 0 f1 ) ( f fN ) ( f f2 ) h 1 h ........... N 1 h 2 2 2 1 f ( x)dx h f 0 f1 f 2 f 2 ........... f N 1 f N O(h 2 ) Trapez Formülü 2 Simpson Formülü: Trapez formülüne göre daha iyi bir yaklaşımla, N sayıda çift alınır ve ardışık iki alt aralık birlikte ele alınırsa; S S elde edilir. x1 x2 xN x0 x1 x N 1 x2 x4 xN x0 x2 x N 2 f ( x)dx f ( x)dx ........... f ( x)dx f ( x)dx f ( x)dx ........... f ( x)dx (*) S s1 s3 s5 .......... sN 1 Trapez kuralını daha sık aralıkla uygulamaktan başka, integrali daha doğru hesaplamak için diğer bir yol, noktaları birleştirmek için daha yüksek dereceli polinomlar kullanmaktır. Örneğin, eğer f(a) ve f(b) noktaları arasında bilinen ek bir nokta varsa(Şekil5.3), bu üç nokta bir parabolle birleştirilebilir. Eğer f(a) ve f(b) arasında eşit aralıklı iki nokta varsa, bu dört nokta üçüncü dereceden bir polinom ile birleştirilebilir. Bu polinomlar altında kalan integralleri veren formüller Simpson Kuralları diye adlandırılır. f(x) f(x) f(b) f(a) parabol a=xi-1 xi b=xi+1 x Şekil 4.4:Sayısal İntegralde Simpson yaklaşımı grafiği. Şekildeki parabol denklemi; f ( x) ( x xi )( x xi 1 ) ( x xi 1 )( x xi 1 ) ( x xi 1 )( x xi ) f i 1 fi f i 1 ( xi 1 xi )( xi 1 xi 1 ) ( xi xi 1 )( xi xi 1 ) ( xi 1 xi 1 )( xi 1 xi ) Bu ifade (*) denkleminde yerine konur ve si integrali analitik olarak alınırsa; si xi1 xi 1 f ( x)dx h fi 1 4 fi fi 1 3 olur. si ifadeleri S integralinde yerine konursa; S h f 0 4 f1 f 2 h f 2 4 f 3 f 4 h f 4 4 f 5 f 6 ........ h f N 2 4 f N 1 f N 3 3 3 3 b a f ( x)dx h f 0 4 f1 2 f 2 4 f3 2 f 4 ......... 4 f N 1 f N O(h 4 ) 3 olarak Simpson Formülü elde edilir. Gauss Integrali: Tüm integral yöntemlerinde sayısal integral aşağıdaki şekilde alınır. b N f ( x)dx w f ( x ) a i 1 i i Trapez ve Simpson yöntemlerinde 100 veya 200 nokta kullanılarak bulunan sonuçlar aynı duyarlıkta, 3 veya 5 nokta kullanılarak Gauss yöntemiyle elde edilebilir. Trapez ve Simpson yöntemlerinde xi noktaları eşit aralıklarla sıralanıyor ve bunlar ağırlık katsayıları 2,4,4,….gibi sabit değerler alıyordu. Gauss yönteminde eşit aralıkta noktalar kullanmak yerine, daha az sayıda nokta kullanılır ve bunların katsayıları farklı alınır. •f(x) fonksiyonunun [-1,1] aralığındaki integralini N=2 noktanın toplamı olarak yazalım: 1 f ( x)dx w f ( x ) w 1 1 1 x1, x2, w1 ve w2 bilinmeyen parametreler. 2 f ( x2 ) 1 1dx 2 w w f (x) 1 1 2 (1) 1 1 f ( x) x xdx 0 w x 1 1 w2 x2 1 1 2 x dx 3 w x 2 f ( x) x 2 2 1 1 w2 x22 (2) (3) 1 1 f ( x) x 3 x dx 0 w x 3 1 3 1 1 w2 x23 (4) (2) Denklemini x12 çarpıp dördüncüden çıkarırsak; w2 x2 ( x2 x1 )( x2 x1 ) 0 Bu eşitliği sağlamak üç şekilde mümkündür. Ya x2=0, veya x1=x2, yada x1=-x2 olmalıdır. İlk iki ifade anlamsızdır, çünkü formül tek noktaya inmiş olur. Bu durumda x1=-x2 alıp diğer bilinmeyenleri bulursak, (2) denkleminden; w1x1+w2x2=0 w1x1=-w2x2 (x1=-x2 alınırsa) w1(-x2)=-w2x2 w1=w2 (1)’den w1+w2=2 w1=w2=1 elde edilir. (3)’den w1x12+w2x22=2/3 w1=w2=1 x12+x22=2/3 x1=-x2 olduğundan, x12+x12=2/3 x1=-x2=0.57735 Böylece, 2-noktalı Gauss integral formülünü şöyle yazabiliriz; 1 f ( x)dx f (0.57735) f (0.57735) 1 Gauss yöntemi ikiden fazla nokta için genişletilebilir. N sayıda nokta için, 1 N f ( x)dx w f ( x ) i 1 1 i i Alıp, yine bu ifadenin x2N-1 dereceye kadar olan polinomlar için tam sonuç vermesini isteyerek katsayılar hesaplanır. Gauss integrali için gerekli xi ve wi değerleri ilk birkaç N sayısı için aşağıdaki tabloda verilmiştir. Gauss yöntemini [-1,1] aralığında elde ettikten sonra, diğer [a,b] aralıkları için de uygulanabilir. Bunu için lineer bir değişken dönüşümü yapılır: u (b a) x (b a) 2 b a du ba dx 2 alınırsa, ba (b a) x (b a) f (u )du f dx 2 1 2 1 elde edilir. Tekil İntegraller: Buraya kadar incelediğimiz integrallerde, açıkça belirtilmese de, sonlu bir [a,b] aralığı ve bu aralıkta ıraksak olmayan bir f(x) fonksiyonu olduğu varsayılmıştı. Uygulamada bu iki koşula uymayan birçok durumla karşılaşılabilir. Örneğin; I f ( x)dx 0 0, aralığı sonsuzdur, bu aralığı bilgisayarda yoktur. 1 I 0 (b a ) N aralığına bölme olanağı 1 dx x Bu integralde ise x=0 noktasında ıraksak olmaktadır. Sayısal integral alındığında f(0) noktasında “sıfıra bölme” hatası verecektir. Sonsuz aralığı sonlu hale getirmede ve ıraksaklığı ortadan kaldırmakta en geçerli yöntem “değişken değişimi” yapmaktır. Sınırları sonsuzda integraller: Bir integralin alt, üst veya her iki sınırı sonsuzda ise, değişken değişimi yapılarak sınırlar sonlu hale getirilir. I 1 1 dx x4 Yukarıdaki integral için değişken değişimi yapılırsa; 1 1 ve du 2 dx u x x 0 0 du u 2 dx 1 1 I 4 dx u 4 (u 2 )du u 2 du u 2 du x 1 1 1 0 Bu durumda bilinen sayısal yöntemlerle integral alınabilir. Sınırda ıraksak integraller: Eğer ıraksaklık görünürde ise, yine değişken değişimi yöntemi kaldırılabilir; 1 Cosx dx x 0 I Bu integral sınırda ıraksaktır, bunun için x=u2, dx=2udu yapılırsa; 1 1 1 Cosx Cos(u 2 ) I dx 2udu 2 Cos(u 2 )du u x 0 0 0 değişken değişimi Nasıl bir değişken değişimi yapılacağının genel bir kuralı yoktur, her probleme göre farklı düşünülmelidir.