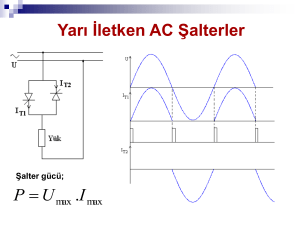
dırac sistemi için bir sınır değer problemi
advertisement

DIRAC SİSTEMİ İÇİN BİR SINIR DEĞER PROBLEMİ
UFUK KAYA
Mersin Üniversitesi
Fen Bilimleri Enstitüsü
Matematik
Ana Bilim Dalı
YÜKSEK LİSANS TEZİ
Tez Danışmanı
Prof. Dr. Nazım KERİMOV
MERSİN
Haziran - 2008
ÖZ
Bu çalışmada Dirac sistemi için, denklemleri ve sınır koşullarından biri
spektral parametre içeren aşağıdaki sınır değer problemi incelenmiştir:
u '− {λ + P ( x )} w = 0 ,
w '+ {λ + R ( x )} u = 0 ,
u ( 0 ) cos α − w ( 0 ) sin α = 0 ,
( λ cos β + a ) u (1) − ( λ sin β + b ) w (1) = 0 .
Burada 0 ≤ x ≤ 1 , λ spektral parametre, P ( x ) ve R ( x ) reel değerli ve C [ 0,1]
π π
sınıfından fonksiyonlar, a, b ∈ , α , β ∈ − , ve a sin β − b cos β < 0 ’dır.
2 2
Bu çalışmada söz konusu problemin:
1. Özdeğerlerin sayılabilir olduğu, bu özdeğerlerin reelliği ve basitliği
ispatlanmış;
2. Özvektör fonksiyonlarının salınım özellikleri incelenmiş;
3. Özdeğer ve özvektör fonksiyonları için asimptotik formüller elde edilmiştir.
Anahtar Kelimeler: Dirac denklemler sistemi, sınır değer problemi, özdeğer
ve özvektör fonksiyonu, salınım, asimptotik formül.
i
ABSTRACT
In this work, we consider the following boundary value problem for the
Dirac system with a spectral parameter in the equation and the boundary condition:
u '− {λ + P ( x )} w = 0 ,
w '+ {λ + R ( x )} u = 0
u ( 0 ) cos α − w ( 0 ) sin α = 0 ,
( λ cos β + a ) u (1) − ( λ sin β + b ) w (1) = 0 .
Where 0 ≤ x ≤ 1 , λ is the spectral parameter, P ( x ) and R ( x ) are real-valued
functions
from
the
class
C [ 0,1] ,
a, b ∈ ,
π π
α , β ∈ − ,
2 2
and
a sin β − b cos β < 0 .
We prove:
1. that there is a countable set of eigenvalues of the given problem and that they
are real and simple;
2. oscillatory properties of the eigen-vector-functions;
3. asymptotik formulas for eigenvalues and eigen-vector-functions with
remainder of the form O ( n −1 ) .
Keywords: Dirac equations system, boundary value problem, eigenvalue and
eigen-vector-function, oscillation, asymptotik formula.
ii
TEŞEKKÜR
Bu çalışmayı hazırlamamda desteğini hiçbir zaman esirgemeyen değerli
danışmanım Prof. Dr. Nazım KERİMOV’a teşekkür ederim. Ayrıca, bu çalışma
boyunca yardımını esirgemeyen bölüm hocalarıma ve araştırma görevlisi
arkadaşlarıma teşekkürlerimi sunarım.
iii
İÇİNDEKİLER
SAYFA
ÖZ…………………………………………………………………………... i
ABSTRACT……………………………………………………………....... ii
TEŞEKKÜR……………………………………………………………......
iii
İÇİNDEKİLER…………………………………………………………….
iv
SİMGELER VE KISALTMALAR…………….........................................
vi
1. GİRİŞ……………………………………………………………………
1
2. KAYNAK ARAŞTIRMASI……………………………………………
2
3. MATERYAL VE METOT…………………………………………….. 3
3.1. ÖN BİLGİLER……………………………………………………… 3
3.1.1. Temel Tanımlar ve Teoremler……………………..................
3
3.1.2. Süreklilik Modülü…………………………………………….
5
3.1.3. Tam Fonksiyonun Tanımı ve Bazı Özellikleri……………….. 7
3.2. BİR BOYUTLU DIRAC SİSTEMİNİN TANIMI VE
ÖZELLİKLERİ ……..………………………………………………
8
3.2.1.Bir Boyutlu Dirac Sisteminin Kanonik Biçime
İndirgenmesi…………………………………………………
8
3.2.2.Sınır Koşulları ile Verilen Dirac Operatörünün Özdeğerleri ve
Özvektör Fonksiyonlarının Bazı Temel Özellikleri………....... 11
3.3. (3.7)-(3.9) SINIR DEĞER PROBLEMİNİN ÖZDEĞERLERİ VE
ÖZVEKTÖR FONKSİYONLARI İÇİN ASİMPTOTİK
FORMÜLLER………………………………………………………
13
3.3.1.Operatör Dönüşümün Tanımı ve Genel İfadesi……………….
13
3.3.2.Operatör Dönüşümün Yardımı ile Asimptotik Formüllerin
Elde Edilmesi………………………………………………….
15
4. BULGULAR VE TARTIŞMA………………………………………… 20
4.1. (1.1)-(1.4) SINIR DEĞER PROBLEMİNİN
ÖZDEĞERLERİNİN BAZI ÖZELLİKLERİ……………………….
20
4.2. BAZI YARDIMCI İDDİALAR.......................................................... 24
iv
4.3. (1.1)-(1.4) SINIR DEĞER PROBLEMİNİN
ÖZFONKSİYONLARININ SALINIM ÖZELLİKLERİ …………..
27
4.4. θ n ( x ) FONKSİYONUNUN TANIMI VE ÖZELLİKLERİ…..........
32
4.5. (1.1)-(1.4) SINIR DEĞER PROBLEMİNİN ÖZDEĞERLERİ VE
ÖZVEKTÖR FONKSİYONLARI İÇİN ASİMPTOTİK
FORMÜLLER………………………………………………………
34
5. SONUÇLAR VE ÖNERİLER…………………………………………
40
KAYNAKLAR……………………………………………………………..
43
ÖZGEÇMİŞ………………………………………………………………... 47
v
SİMGELER VE KISALTMALAR
{1, 2, 3,...} doğal sayılar kümesi
{..., −2, −1, 0,1, 2,...} tam sayılar kümesi
Reel sayılar kümesi
n
’nin kendisiyle n kez kartezyen çarpımı
Kompleks sayılar kümesi
Ι
Birim operatör
z
z kompleks sayısının eşleniği
arg z
z kompleks sayısının argümenti
( f , g)
f ile g vektörlerinin bulundukları uzaydaki iç çarpımı
∞
{an }n=1
{an : n ∈ }
( a, b )
{ x ∈ : a < x < b}
[ a, b )
{ x ∈ : a ≤ x < b}
( a, b ]
{ x ∈ : a < x ≤ b}
[ a, b ]
{ x ∈ : a ≤ x ≤ b}
C [ a, b ]
[ a, b ]
kapalı aralığında sürekli ve reel değerli tüm fonksiyonların
uzayı
O ( an )
Landau sembolü
f ( x ) ≡ g ( x ) Her bir x ∈ [ a, b ]
f −1
([ a, b ) , ( a, b ] , [ a, b]) için f ( x ) = g ( x )
f fonksiyonunun (operatörünün) tersi
sup
Üst sınırların en küçüğü (supremum)
inf
Alt sınırların en büyüğü (infimum)
vi
1. GİRİŞ
Lineer diferansiyel operatörlerin spektral teorisinin önemli problemlerinden
biri, sınır koşulları spektral parametre içeren sınır değer probleminin bazı temel
spektral özelliklerinin (özdeğerlerinin ve özfonksiyonlarının varlığı, onların
asimptotik gösterimleri, özfonksiyonlarının salınım özellikleri vs.) incelenmesidir.
Bu tez çalışmasında
u '− {λ + P ( x )} w = 0 ,
(1.1)
w '+ {λ + R ( x )} u = 0 ,
(1.2)
u ( 0 ) cos α − w ( 0 ) sin α = 0 ,
(1.3)
( λ cos β + a ) u (1) − ( λ sin β + b ) w (1) = 0
(1.4)
şeklindeki spektral problemin yukarıda gösterilmiş tür spektral özellikleri
incelenecektir.
Burada 0 ≤ x ≤ 1 , λ
spektral parametre,
P ( x)
R ( x)
ve
fonksiyonları [ 0,1] kapalı aralığında reel değerli sürekli fonksiyonlar, a, b belirli
reel sayılar ve −
π
2
≤α ≤
π
2
,−
π
2
≤β ≤
π
2
’dir.
(1.1) - (1.4) sınır değer probleminin spektral özelliklerinin incelenmesi
σ = a sin β − b cos β < 0
(1.5)
koşulu dahilinde yapılacaktır.
Not 1.1. Belirtelim ki; a0 , b0 , a1 , b1 , c1 , d1 , ( a02 + b02 > 0, a12 + c12 > 0 ) belirli
reel sayılar olmak üzere
a0u ( 0 ) − b0 w ( 0 ) = 0 ,
( a1λ + b1 ) u (1) − ( c1λ + d1 ) w (1) = 0
şekilli sınır koşulları (1.3) - (1.4) şekilli sınır koşullarına dönüştürülebilir. Bu
durumda (1.5) koşulunun sağlanması için
b1c1 − d1a1 < 0
olmalıdır.
1
(1.6)
2. KAYNAK ARAŞTIRMASI
Lineer diferansiyel operatörlerin spektral özelliklerinin incelenmesi hakkında
yapılan ilk temel çalışmalar [1-3] kaynaklarında düzenlenmiştir. Sturm - Liouville
tipli diferansiyel operatörler için 1973 yılında J. Walter [4] sınır koşullarından biri,
1977 yılında C.T. Fulton [5] ve 1993 yılında P.J. Browne, P.A. Binding, K. Seddighi
[15] sınır koşullarından her ikisi spektral parametre içeren sınır değer problemlerini
incelemişlerdir. [6], [7], [8], [9], [10], [11], [12], [16], [17], [18], [19], [20], [21],
[22], [23], [24], [25], [26] çalışmalarında sınır koşullarında spektral parametre içeren
Sturm – Liouville tipli diferansiyel operatörler incelenmiştir. Özellikle [16] ve [17]
çalışmalarında sınır koşullarından her ikisi de λ spektral parametresinin lineer
olmayan kuadratik fonksiyonunu içerir.
[13] ve [14] çalışmalarında dördüncü mertebeden adi diferansiyel operatörler
için dört sınır koşulundan biri spektral parametre içeren sınır değer problemi
incelenmiş ve bir dizi sonuçlar elde edilmiştir.
[27] çalışmasında kısmi diferansiyel denklem olarak verilen ısı denklemi
değişkenlere ayırma metodu kullanılarak sınır koşullarından biri spektral parametre
içeren Sturm–Liouville tipli spektral probleme indirgenmiştir.
Dirac sistemi için 2002 yılında N.B. Kerimov [28] sınır koşullarından her
ikisi spektral parametre içeren sınır değer probleminin spektral özelliklerine ait
sonuçlar elde etmiştir.
2
3. MATERYAL VE METOD
3.1. ÖN BİLGİLER
3.1.1 Temel Tanımlar ve Teoremler
f , ( a, b ) açık aralığında tanımlı, reel değerli bir
Tanım 3.1.1.1 [29].
fonksiyon ve x0 ∈ ( a, b ) olsun. Her bir ε > 0 sayısına karşılık x − x0 < δ iken
f ( x ) − f ( x0 ) < ε olacak biçimde bir δ = δ ( ε , x0 ) > 0 sayısı bulunabilirse f
fonksiyonuna x0 noktasında süreklidir denir.
f , ( a, b ) açık aralığında tanımlı, reel değerli bir
Tanım 3.1.1.2 [29].
fonksiyon olsun.
f fonksiyonu ( a, b ) aralığının her bir noktasında sürekli ise f
fonksiyonuna ( a, b ) aralığında süreklidir denir.
f , ( a, b ) açık aralığında tanımlı, reel değerli bir
Tanım 3.1.1.3 [29].
fonksiyon ve x0 ∈ ( a, b ) olsun.
(δ < x − x0 ≤ 0 )
Her bir ε > 0 sayısına karşılık 0 ≤ x − x0 < δ
iken f ( x ) − f ( x0 ) < ε olacak biçimde bir δ = δ ( ε , x0 ) > 0 sayısı
bulunabilirse f fonksiyonuna x0 noktasında sağdan (soldan) süreklidir denir.
Tanım 3.1.1.4 [29].
fonksiyon olsun.
f , [ a, b] kapalı aralığında tanımlı, reel değerli bir
f , ( a, b ) açık aralığında sürekli, x = a noktasında sağdan ve
x = b noktasında soldan sürekli ise f
fonksiyonuna
[ a, b ]
kapalı aralığında
süreklidir denir.
[ a, b ]
kapalı aralığında sürekli ve reel değerli bütün fonksiyonların kümesi
C [ a, b ] gösterilir.
3
Tanım 3.1.1.5 [29].
f,
( a, b )
(ya da [ a, b] ) aralığında tanımlı, reel
değerli bir fonksiyon olsun. Her bir ε > 0 sayısına karşılık x′ − x′′ < δ koşulunu
sağlayan her x′, x′′ ∈ ( a, b ) (ya da x′, x′′ ∈ [ a, b] ) için
f ( x′ ) − f ( x′′ ) < ε olacak
şekilde bir δ = δ ( ε ) > 0 sayısı bulunabilirse f fonksiyonuna ( a, b ) (ya da [ a, b ] )
aralığında düzgün süreklidir denir.
Teorem 3.1.1.1 [29] (Cantor Teoremi). Kapalı aralıkta sürekli olan her
fonksiyon düzgün süreklidir.
Teorem 3.1.1.2 [29] (Ara Değer Teoremi). f ∈ C [ a, b ] olsun.
[ a, b] ’de
x1 < x2 ve f ( x1 ) ≠ f ( x2 ) olacak şekilde herhangi iki x1 , x2 noktası verildiğinde f
fonksiyonu ( x1 , x2 ) aralığında, f ( x1 ) ile f ( x2 ) arasındaki her değeri en az bir defa
alır.
Tanım 3.1.1.6 [30].
f,
( a, b )
aralığında tanımlı bir fonksiyon ve
x0 ∈ ( a, b ) olsun. Eğer
lim
x → x0
f ( x ) − f ( x0 )
x − x0
limiti var ve sonlu ise f fonksiyonuna x0 noktasında türevlenebilirdir denir. Bu
durumda
f ′ ( x0 ) = lim
x → x0
f ( x ) − f ( x0 )
x − x0
yazılır.
Teorem 3.1.1.3 [30] (Rolle Teoremi). f , [ a, b] kapalı aralığında sürekli
( a, b )
açık aralığında türevlenebilir bir fonksiyon ve f ( a ) = f ( b ) olsun.
durumda f ′ ( c ) = 0 olacak şekilde en az bir c ∈ ( a, b ) vardır.
4
Bu
Teorem 3.1.1.4 [30] (Diferansiyel Hesabın Ortalama Değer Teoremi).
f,
[ a, b ]
( a, b )
kapalı aralığında sürekli,
açık aralığında türevlenebilir bir
fonksiyon olsun. Bu durumda,
f ′(c) =
f (b ) − f ( a )
b−a
olacak şekilde en az bir c ∈ ( a, b ) vardır.
Tanım 3.1.1.7 [29].
f , A ⊂ kümesinde tanımlı bir fonksiyon olsun.
Her bir x ∈ A için f ( x ) ≤ M olacak şekilde en az bir M > 0 sayısı varsa f
fonksiyonuna A kümesi üzerinde sınırlıdır denir. Aksi durumda f fonksiyonuna
A kümesi üzerinde sınırsızdır denir.
Tanım 3.1.1.8 [29]. Eğer A ⊂ üstten (alttan) sınırlı bir küme ise A ’nın
üst sınırların en küçüğüne (alt sınırlarının en büyüğüne) A ’nın supremumu
(infimumu) denir ve sup A ( inf A) ile gösterilir.
Teorem 3.1.1.5 [29] (Weierstrass Teoremi).
f ∈ C [ a, b ] ise
f
fonksiyonu [ a, b] kapalı aralığında sınırlıdır.
Tanım 3.1.1.9 [29].
doğal sayılar kümesi üzerinde tanımlı bir
fonksiyona dizi denir. f bir dizi ise her bir n doğal sayısına bir an = f ( n ) elemanı
∞
karşılık geleceğinden f dizisi {an }n =1 şeklinde gösterilebilir.
3.1.2. Süreklilik Modülü
Tanım 3.1.2.1 [31].
f fonksiyonu [ a, b] kapalı aralığında sürekli olsun.
[ 0, b − a ] aralığında tanımlı
ω ( f , δ ) = sup f ( x + h ) − f ( x )
a ≤ x ≤b − h
0 ≤ h ≤δ
5
ya da ona denk olan
ω ( f , δ ) = sup
x2 − x1 ≤δ
x1 , x2 ∈[ a ,b ]
f ( x2 ) − f ( x1 )
ile tanımlı ω ( f , δ ) = ω (δ ) fonksiyonuna f fonksiyonunun süreklilik modülü
denir.
Bu tanıma göre ω ( f , δ ) süreklilik modülü δ ∈ [ 0,b − a ] olmak üzere f
fonksiyonunun, uzunluğu δ ’ya eşit olan
[ a, b ]
kapalı aralığının bütün alt
aralıklarındaki maksimum salınımını verir. Buradan her x, x + h ∈ [ a, b ] için
f ( x + h ) − f ( x ) ≤ ω (δ )
ya da her x1 , x2 ∈ [ a, b ] için
f ( x2 ) − f ( x1 ) ≤ ω ( x2 − x1 )
elde edilir.
Bu tanım, fonksiyonun düzgün sürekli olması koşuluyla
( −∞, +∞ )
aralığında da verilebilir.
Örnek 3.1.2.1 [31]. a, b ∈ keyfi sabitler olmak üzere f ( x ) = ax + b ,
x ∈ ( −∞, +∞ ) olsun. Bu durumda herhangi bir δ ≥ 0 için
ω (δ ) = sup a ( x + h ) + b − ax − b = sup ah = a δ
0 ≤ h ≤δ
x∈
0 ≤ h ≤δ
dir.
Örnek 3.1.2.2 [31].
f ( x ) = sin x , x ∈ ( −∞, +∞ ) olsun.
Bu durumda
herhangi bir δ ≥ 0 için
h
h
h
ω (δ ) = sup sin ( x + h ) − sin x = 2 sup cos x + sin = 2 sup sin
2
2
2
x∈
x∈
0 ≤ h ≤δ
0 ≤ h ≤δ
0 ≤ h ≤δ
bulunur. Buradan
δ
2sin , δ < π
ω (δ ) =
2
2 , δ ≥ π
6
elde edilir.
Önerme 3.1.2.1 (Süreklilik Modülünün Özellikleri).
1. ω ( 0 ) = 0 ,
2. ω (δ ) azalmayan bir fonksiyondur,
3. ω (δ ) ∈ C [ 0, b − a ] ,
4. ω (δ ) alt toplamsaldır; yani, her δ1 , δ 2 ≥ 0 için
ω ( δ1 + δ 2 ) ≤ ω ( δ 1 ) + ω ( δ 2 )
sağlanır. Son eşitsizlikten
ω (δ1 + δ 2 + ⋅⋅⋅ + δ n ) ≤ ω (δ1 ) + ω (δ 2 ) + ⋅⋅⋅ + ω (δ n )
genel eşitsizliği elde edilir.
Ayrıca bu genel eşitsizlikte δ1 = δ 2 = ⋅⋅⋅ = δ n = δ
yazılırsa
ω ( nδ ) ≤ nω (δ )
bulunur.
3.1.3. Tam Fonksiyonun Tanımı ve Bazı Özellikleri
Tanım 3.1.3.1 [32]. D ⊂ bir bölge, f : D → bir fonksiyon, z0 ∈ D
olsun. Eğer
lim
z → z0
limiti var ve sonlu ise
f
f ( z ) − f ( z0 )
z − z0
fonksiyonuna z0 ∈ D
noktasında -anlamında
türevlenebilirdir denir.
Tanım 3.1.3.2 [32].
D ⊂ bir bölge f : D → bir fonksiyon olsun.
Eğer f fonksiyonu D bölgesinin her noktasında türevlenebilir ise f fonksiyonuna
D bölgesinde analitiktir (holomorftur) denir.
D bölgesinde analitik olan bütün fonksiyonların kümesi H ( D ) ile
gösterilir.
7
Tanım 3.1.3.3 [32]. Tüm ’de analitik olan fonksiyona tam fonksiyon
denir.
Teorem 3.1.3.1 [32] (Analitik Fonksiyonların Teklik Teoremi).
D ⊂ bir bölge, f , g ∈ H ( D ) olsun. Eğer f ve g fonksiyonları, D
bölgesinde en az bir limit noktasına sahip olan bir küme üzerinde eşit oluyorlarsa,
her z ∈ D için f ( z ) = g ( z ) ’dir.
D ⊂ bir bölge, f ∈ H ( D ) özdeş olarak sıfır
Sonuç 3.1.3.1 [32].
olmayan bir fonksiyon ise, f fonksiyonun D ’de en fazla sayılabilir tane sıfırı
vardır ve bu sıfırların D bölgesinde yerleşen bir limit noktası yoktur.
Sonuç 3.1.3.2 [32]. Özdeş olarak sıfır olmayan bir tam fonksiyonun ’de
en fazla sayılabilir tane sıfırı vardır ve bu sıfırlar sonlu limit noktasına sahip değildir.
3.2. BİR BOYUTLU DIRAC SİSTEMİNİN TANIMI VE ÖZELLİKLERİ
3.2.1. Bir Boyutlu Dirac Sisteminin Kanonik Biçime İndirgenmesi
pik : [ 0, π ] → ( i, k = 1, 2 ) sürekli fonksiyonlar olmak üzere,
p ( x)
L ≡ 11
p21 ( x )
p12 ( x )
, p12 ( x ) ≡ p21 ( x )
p22 ( x )
(3.1)
matris dönüşümünü göz önüne alalım. y ( x ) ile iki komponente sahip
y1 ( x )
y ( x) =
y ( x )
2
vektör fonksiyonunu gösterelim.
0
1
1 0
λ bir parametre, B =
ve I =
−1 0
0 1
olmak üzere
d
B + L − λI y = 0
dx
8
(3.2)
denklemini ele alalım. Bu denklem birinci mertebeden
dy2
+ p11 ( x ) y1 + p12 ( x ) y2 = λ y1 ,
dx
dy
− 1 + p21 ( x ) y1 + p22 ( x ) y2 = λ y2
dx
(3.3)
denklemler sistemine denktir.
p12 ( x ) = p21 ( x ) ≡ 0, p11 ( x ) = V ( x ) + m, p22 ( x ) = V ( x ) − m
durumunda (3.3) denklemler sistemi, göreli kuantum teorisinde “Bir Boyutlu
Durağan Dirac Sistemi” olarak bilinir. Burada V ( x ) potansiyel fonksiyonu ve m
parçacığın kütlesidir.
H = H ( x ) ile 2 ’deki bir düzgün ortogonal dönüşümü gösterelim.
Bilindiği gibi 2 ’deki her ortogonal dönüşüm
cos ϕ ( x ) − sin ϕ ( x )
H ( x) =
sin ϕ ( x ) cos ϕ ( x )
formundadır.
yazalım.
Kolayca gösterilebilir ki BH = HB ’dir ve H −1 vardır.
y = Hz
(3.2)’de y = Hz yerine yazılır ve eşitliğin her iki tarafından H −1
dönüşümü uygulanırsa
H −1 B
d
( Hz ) + H −1 LHz = H −1λ Hz
dx
ya da
B
dz −1 d
+ H B H + H −1 LH z = λ z
dx
dx
elde edilir.
Q = H −1 B
d
H + H −1 LH
dx
yazalım. Kolayca gösterilebilir ki
H −1 B
0
ϕ ′ ( x )
d
H =
ϕ′( x)
dx
0
ve
9
(3.4)
p11 cos 2 ϕ + p12 sin 2ϕ + p22 sin 2 ϕ
H −1 LH =
p cos 2ϕ + 1 ( p − p ) sin 2ϕ
12
22
11
2
1
( p22 − p11 ) sin 2ϕ
2
2
2
p11 sin ϕ − p12 sin 2ϕ + p22 cos ϕ
p12 cos 2ϕ +
dir. Buradan Q matrisinin
q ( x ) q12 ( x )
Q = 11
q21 ( x ) q22 ( x )
1
′
2
2
p12 cos 2ϕ + ( p22 − p11 ) sin 2ϕ
ϕ + p11 cos ϕ + p12 sin 2ϕ + p22 sin ϕ
2
=
1
2
2
ϕ ′ + p11 sin ϕ − p12 sin 2ϕ + p22 cos ϕ
p12 cos 2ϕ + ( p22 − p11 ) sin 2ϕ
2
formunda olduğu elde edilir.
ϕ ( x ) fonksiyonu öyle seçilmelidir ki, q12 ( x ) ≡ 0
olsun. O halde
p12 ( x ) cos 2ϕ ( x ) +
1
{ p22 ( x ) − p11 ( x )} sin 2ϕ ( x ) = 0
2
olur. Buradan
1
2
ϕ ( x ) = arctan
2 p12 ( x )
p22 ( x ) − p11 ( x )
bulunur. O halde Q = Q ( x ) matrisi
q ( x)
0 − p ( x)
0
Q ( x ) = 11
≡
q22 ( x ) 0
−r ( x )
0
olarak düşünülebilir. Buradan (3.4) denklemi
0
0 1 dz − p ( x )
z = λz
+ 0
−r ( x )
−1 0 dx
(3.5)
formunda yeniden yazılabilir. Şimdi ϕ ( x ) fonksiyonunu q11 ( x ) + q22 ( x ) = 0 olacak
biçimde seçelim. Yani 2ϕ ′ ( x ) + p11 ( x ) + p22 ( x ) = 0 olsun. O halde
x
1
ϕ ( x ) = − ∫ { p11 ( t ) + p22 ( t )} dt
20
olur. Buradan (3.4) denkleminin
0 1 dz p ( x ) q ( x )
z = λz
+
−1 0 dx q ( x ) − p ( x )
10
(3.6)
formunda olduğu elde edilir.
(3.5) ve (3.6) denklemlerine (3.2) denkleminin kanonik formu denir. (3.2)
denkleminin çeşitli spektral özellikleri araştırılırken bu kanonik formlardan uygun
olanı kullanılır. Örneğin (3.2) denkleminin özdeğerlerinin ve özfonksiyonlarının
asimptotik davranışlarını araştırırken veya keyfi bir vektör fonksiyonunun (3.2)
denkleminin özvektör fonksiyonlarına göre ayrışım formüllerini incelerken (3.5)
kanonik formunu kullanmak uygun olur.
Buna karşılık (3.2) denkleminin
özdeğerlerinin sayısının asimptotik davranışları ile ilgili problemlerde ve sonsuz
aralıklar üzerindeki ters problemlerde (3.6) kanonik formunu kullanmak daha uygun
olur [2].
3.2.2. Sınır Koşulları ile Verilen Dirac Operatörünün Özdeğerleri ve
Özvektör Fonksiyonlarının Bazı Temel Özellikleri
p ( x ) ve r ( x ) ,
[0, π ]
aralığında sürekli, reel değerli fonksiyonlar ve
α , β ∈ olmak üzere (3.3) denklemler sistemi için (3.5) kanonik formunun
kullanıldığı aşağıdaki sınır değer problemini göz önüne alalım:
y2′ − {λ + p ( x )} y1 = 0, y1′ + {λ + r ( x )} y2 = 0,
(3.7)
y2 ( 0 ) cos α + y1 ( 0 ) sin α = 0,
(3.8)
y2 (π ) cos β + y1 (π ) sin β = 0.
(3.9)
Varsayalım ki λ = λ1 sayısı için (3.7) - (3.9) sınır değer problemi, aşikardan
farklı
y1 ( x, λ1 )
y ( x, λ1 ) =
y ( x, λ )
1
2
çözümüne sahiptir.
Bu durumda λ1 sayısına özdeğer ve
y ( x, λ1 ) vektör
fonksiyonuna da λ1 özdeğerine karşılık gelen özvektör fonksiyonu denir [2].
11
Lemma 3.2.2.1 [2].
(3.7) - (3.9) sınır değer probleminin farklı λ1 , λ2
özdeğerlerine karşılık gelen
y ( x, λ1 )
z ( x, λ2 )
ile
özvektör fonksiyonları
ortogonaldir. Yani
π
∫ { y ( x, λ ) z ( x, λ ) + y ( x, λ ) z ( x, λ )} dx = 0
1
1
1
2
2
1
2
2
0
dır.
İspat: y ( x, λ1 ) ve z ( x, λ2 ) vektör fonksiyonları (3.7) denklemlerinin
çözümü olduğundan
y2′ ( x, λ1 ) − {λ1 + p ( x )} y1 ( x, λ1 ) = 0,
y1′ ( x, λ1 ) + {λ1 + r ( x )} y2 ( x, λ1 ) = 0,
z2′ ( x, λ2 ) − {λ2 + p ( x )} z1 ( x, λ2 ) = 0,
z1′ ( x, λ2 ) + {λ2 + r ( x )} z2 ( x, λ2 ) = 0
sağlanır.
Bu denklemler sırasıyla
z1 ( x, λ2 ) , − z2 ( x, λ2 ) , − y1 ( x, λ1 ) , y2 ( x, λ1 )
fonksiyonları ile çarpılıp taraf tarafa toplanırsa
d
{ y1 ( x, λ1 ) z2 ( x, λ2 ) − y2 ( x, λ1 ) z1 ( x, λ2 )}
dx
= ( λ1 − λ2 ) { y1 ( x, λ1 ) z1 ( x, λ2 ) + y2 ( x, λ1 ) z2 ( x, λ2 )}
elde edilir. Son eşitliğin iki tarafı 0’dan π ’ye integre edilirse
π
( λ1 − λ2 ) ∫ { y1 ( x, λ1 ) z1 ( x, λ2 ) + y2 ( x, λ1 ) z2 ( x, λ2 )} dx
0
= { y1 ( x, λ1 ) z2 ( x, λ2 ) − y2 ( x, λ1 ) z1 ( x, λ2 )}
π
0
olur. Eşitliğin sağ tarafı (3.8) - (3.9) sınır koşullarından dolayı 0 olur. O halde
π
( λ1 − λ2 ) ∫ { y1 ( x, λ1 ) z1 ( x, λ2 ) + y2 ( x, λ1 ) z2 ( x, λ2 )} dx = 0
(3.10)
0
dır. λ1 ≠ λ2 olduğundan (3.10) eşitliğinin her iki tarafı ( λ1 − λ2 ) sayısına bölünürse
π
∫ { y ( x, λ ) z ( x, λ ) + y ( x, λ ) z ( x, λ )} dx = 0
1
1
1
2
2
0
12
1
2
2
elde edilir.
Bu ise y ( x, λ1 ) ile z ( x, λ2 ) özvektör fonksiyonlarının ortogonal
olduğunu gösterir.
Lemma 3.2.2.2 [2]. (3.7) - (3.9) sınır değer probleminin özdeğerleri reeldir.
İspat: λ0 sayısı (3.7) - (3.9) sınır değer probleminin bir özdeğeri ve y ( x, λ0 )
bu özdeğere karşılık gelen özvektör fonksiyonu olsun. O halde y ( x, λ0 ) ≡/ 0 ’dır.
Kolayca gösterilebilir ki, λ0 sayısı da (3.7) - (3.9) sınır değer probleminin bir
özdeğeridir ve bu özdeğere karşılık gelen özvektör fonksiyonu y ( x, λ0 ) ’dir. Bu
bilgilere göre (3.10) denklemi
π
(λ
0 − λ0
) ∫ { y ( x, λ )
1
0
2
+ y2 ( x, λ0 )
0
2
} dx = 0
halini alır. y ( x, λ0 ) ≡/ 0 olduğundan
π
∫ { y ( x, λ )
1
0
2
+ y2 ( x, λ0 )
0
2
} dx > 0
dır. O halde λ0 − λ0 = 0 , yani λ0 = λ0 ‘dir. Buradan λ0 ∈ elde edilir.
3.3. (3.7) - (3.9) SINIR DEĞER PROBLEMİNİN ÖZDEĞERLERİ VE
ÖZVEKTÖR FONKSİYONLARI İÇİN ASİMPTOTİK FORMÜLLER
3.3.1. Operatör Dönüşümün Tanımı ve Genel İfadesi
Tanım 3.3.1.1 [2]. A ve B iki lineer diferansiyel operatör, Φ1 ve Φ 2 iki
lineer fonksiyon uzayı, X ise Φ1 ’den Φ 2 ’ye bir sürekli lineer dönüşüm olsun ve
aşağıdaki koşulları sağlasın:
1o AX = XB ’dir
2o X −1 sürekli tersi vardır.
Bu durumda, X ’e bir operatör dönüşüm denir.
13
d
d
p1 ( x ) dx
p2 ( x )
dx
A≡
, B ≡
d
−d
r1 ( x )
r2 ( x )
−
dx
dx
(3.11)
olsun. Burada p1 ( x ) , p2 ( x ) , r1 ( x ) ve r2 ( x ) , [ 0, π ] aralığında sürekli ve reel
değerli fonksiyonlardır.
Φ1 ve Φ 2 sırasıyla
f 2 ( 0 ) cos γ + f1 ( 0 ) sin γ = 0,
g 2 ( 0 ) cos δ + g1 ( 0 ) sin δ = 0
(3.12)
sınır koşullarını sağlayan ve
f1 ( x )
g1 ( x )
f ( x) =
, g ( x) =
f ( x)
g ( x )
2
2
sürekli türevlere sahip olan fonksiyonların uzayı olsun. Burada γ ve δ keyfi reel
sayılardır [2].
Lemma 3.3.1.1 [2]. Bir X operatör dönüşümü g ( x ) = X f ( x ) şeklinde
verilir. Yani
x
g1 ( x ) = α ( x ) f1 ( x ) + β ( x ) f 2 ( x ) + ∫ { P ( x, s ) f1 ( s ) + R ( x, s ) f 2 ( s )} ds,
0
(3.13)
x
g 2 ( x ) = − β ( x ) f1 ( x ) + α ( x ) f 2 ( x ) + ∫ {Q ( x, s ) f1 ( s ) + H ( x, s ) f 2 ( s )} ds
0
dir. Burada
1 x
1
sin ∫ p1 ( t ) + r1 ( t ) − p2 ( t ) − r2 ( t ) dt + arcsin ,
χ
χ
2 0
1 x
1
1
β ( x ) = cos ∫ p1 ( t ) + r1 ( t ) − p2 ( t ) − r2 ( t ) dt + arcsin
χ
χ
2 0
α ( x) =
1
(3.14)
dır. Ayrıca χ = sec ( δ − γ ) ve P ( x, s ) , R ( x, s ) , Q ( x, s ) , H ( x, s ) sürekli türeve
sahip fonksiyonlardır.
Bu iddianın ispatı [2, pp:367-372]’da yapılmıştır.
14
3.3.2. Operatör Dönüşümün Yardımı ile Asimptotik Formüllerin Elde
Edilmesi
ϕ1 ( x, λ )
vektör fonksiyonu (3.7) denklemler sisteminin
ϕ ( x, λ )
2
ϕ ( x, λ ) =
ϕ1 ( 0, λ ) = cos α , ϕ 2 ( 0, λ ) = − sin α
(3.15)
koşullarını sağlayan çözümü olsun. p ( x ) = r ( x ) ≡ 0 için
ϕ1 ( x, λ ) = cos ( λ x − α ) , ϕ2 ( x, λ ) = sin ( λ x − α )
(3.16)
olduğunu göstermek zor değildir. Şimdi (3.7) - (3.8) probleminin çözümlerine bir
operatör dönüşümü uygulayalım. (3.7) denklemler sistemi
d
− p ( x)
dx
A1 y =
y = λy
−d
−r ( x )
dx
(3.17)
formundadır. (3.16) fonksiyonu, yani
cos ( λ x − α )
sin ( λ x − α )
vektör fonksiyonu
0
B1 y =
− d
dx
d
dx
y = λy
0
(3.18)
denkleminin çözümüdür. Eğer ψ ( x, λ ) vektör fonksiyonu B1ψ = λψ denkleminin
bir çözümü ise X operatör dönüşümünün tanımı kullanılarak
A1 X [ψ ] = XB1 [ψ ] = X [ λψ ] = λ X [ψ ]
olduğu elde edilir. Yani ϕ = X [ψ ] vektör fonksiyonu A1ϕ = λϕ denkleminin bir
çözümüdür. Böylece
cos ( λ x − α )
sin ( λ x − α )
ψ ( x, λ ) =
15
vektör fonksiyonu (3.18) denkleminin bir çözümü ise ϕ ( x, λ ) = X ψ ( x, λ ) vektör
fonksiyonu da (3.17) denkleminin bir çözümüdür.
Ele alınan bu durumda,
p1 ( x ) = − p ( x ) , r1 ( x ) = −r ( x ) , p2 ( x ) = r2 ( x ) ≡ 0 ’dır ve (3.12) sınır koşullarının
yerine, (3.15) sınır koşulları alındığından γ = δ olur. Yani χ = 1 ’dir. (3.14) ’ten
1
x
∫ p ( t ) + r ( t ) dt ,
2
α ( x ) = cos
0
1
β ( x ) = sin ∫ p ( t ) + r ( t ) dt
2 0
x
(3.19)
elde edilir. (3.13) formülünden (3.7), (3.15) probleminin
ϕ1 ( x, λ )
ϕ ( x, λ )
2
ϕ ( x, λ ) =
çözümü için aşağıdaki formüller elde edilir:
ϕ1 ( x, λ ) = α ( x ) cos ( λ x − α ) + β ( x ) sin ( λ x − α )
x
+ ∫ {P ( x, s ) cos ( λ s − α ) + R ( x, s ) sin ( λ s − α )} ds ,
0
ϕ2 ( x, λ ) = α ( x ) sin ( λ x − α ) − β ( x ) cos ( λ x − α )
x
+ ∫ {Q ( x, s ) cos ( λ s − α ) + H ( x, s ) sin ( λ s − α )} ds .
0
Ya da (3.19)’daki α ( x ) ve β ( x ) değerleri yerine yazılırsa
ϕ1 ( x, λ ) = cos {ξ ( x, λ ) − α }
x
+ ∫ {P ( x, s ) cos ( λ s − α ) + R ( x, s ) sin ( λ s − α )} ds
(3.20)
0
ϕ2 ( x, λ ) = sin {ξ ( x, λ ) − α }
x
+ ∫ {Q ( x, s ) cos ( λ s − α ) + H ( x, s ) sin ( λ s − α )} ds
(3.21)
0
elde edilir. Burada
x
1
ξ ( x, λ ) = λ x − ∫ { p ( t ) + r ( t )} dt
20
dir.
16
(3.22)
Lemma 3.3.2.1. [2]. Aşağıdaki asimptotik formüller doğrudur.
1
ϕ1 ( x, λ ) = cos {ξ ( x, λ ) − α } + O ,
λ
(3.23)
1
ϕ2 ( x, λ ) = sin {ξ ( x, λ ) − α } + O ,
λ
∂ϕ1 ( x, λ )
= − x sin {ξ ( x, λ ) − α } + O (1) ,
∂λ
∂ϕ2 ( x, λ )
= x cos {ξ ( x, λ ) − α } + O (1) .
∂λ
(3.24)
İspat: (3.23)’ü elde etmek için (3.20) ve (3.21)’in sağ tarafındaki
integrallerde kısmi integrasyon yöntemini kullanmak yeterlidir. ( P ( x, s ) , R ( x, s ) ,
Q ( x, s )
ve
H ( x, s )
fonksiyonları
diferansiyellenebilir olduğundan
kısmi
integrasyon metodu uygulanabilir). (3.24) ise (3.20) ve (3.21)’in iki yanından türev
alınarak benzer bir yolla ispatlanabilir.
Lemma 3.3.2.2 [2]. (3.7) - (3.9) sınır değer probleminin özdeğerleri sadece
ϕ2 (π , λ ) cos β + ϕ1 (π , λ ) sin β
fonksiyonunun sıfırlarıdır ve bu fonksiyonun bütün sıfırları basittir.
İspat:
ϕ1 ( x, λ )
ve
ϕ 2 ( x, λ )
fonksiyonları
(3.8)
sınır
koşullarını
sağladığından (3.7) - (3.9) sınır değer probleminin özdeğerlerini bulmak için
ϕ1 ( x, λ ) ve ϕ2 ( x, λ ) fonksiyonlarına (3.9) sınır koşulları sağlatılmalı ve ardından
bu denklemin sıfırları araştırılmalıdır.
D ( λ ) = ϕ2 (π , λ ) cos β + ϕ1 (π , λ ) sin β
yazılırsa
dD ( λ ) ∂ϕ2 (π , λ )
∂ϕ (π , λ )
=
cos β + 1
sin β
dλ
∂λ
∂λ
elde edilir. Varsayalım ki, λ1 sayısı D ( λ ) fonksiyonunun çok katlı köküdür ve
17
ϕ1 ( x, λ1 )
ϕ ( x, λ )
1
2
ϕ ( x, λ1 ) =
λ1 özdeğerine karşılık gelen özvektör fonksiyonudur.
dD ( λ1 )
dλ
O halde D ( λ1 ) = 0 ve
= 0 denklemlerinin ikisi aynı anda sağlanır. Yani
ϕ2 (π , λ1 ) cos β + ϕ1 (π , λ1 ) sin β = 0
ve
∂ϕ2 (π , λ1 )
∂λ
cos β +
∂ϕ1 (π , λ1 )
∂λ
sin β = 0
dır. Bu iki denklemden
ϕ2 (π , λ1 )
∂ϕ1 (π , λ1 )
∂λ
− ϕ1 ( π , λ1 )
∂ϕ2 (π , λ1 )
∂λ
=0
(3.25)
elde edilir. (3.7) denkleminin her iki tarafından λ ’ya göre türev alınırsa
∂y1
∂y2 ′
= y1 ,
− {λ + p ( x )}
∂λ
∂λ x
(3.26)
∂y2
∂y1 ′
= − y2
+ {λ + r ( x )}
∂λ
∂λ x
elde edilir. (3.7) ve (3.26) denklemleri sırasıyla
∂y1
∂y
, − 2 , − y1 ve y2 ile çarpılıp
∂λ
∂λ
taraf tarafa toplanır ve daha sonra 0’dan π ’ye integre edilirse
π
∂y1
∂y
− y1 ( x, λ ) 2
y2 ( x , λ )
∂λ
∂λ
π
= − ∫ { y12 ( x, λ ) + y2 2 ( x, λ )} dx
0
0
elde edilir. λ = λ1 değeri yerine yazılırsa (3.15)’ten
∂ϕ1 ( x, λ1 )
∂λ
=
x=0
∂ϕ 2 ( x, λ1 )
∂λ
=0
x =0
olacağından (3.25) denkleminden
π
− ∫ {ϕ12 ( x, λ1 ) + ϕ 2 2 ( x, λ1 )} dx = ϕ 2 (π , λ1 )
0
∂ϕ1 (π , λ1 )
∂ϕ (π , λ1 )
− ϕ1 (π , λ1 ) 2
=0
∂λ
∂λ
elde edilir. Buradan ϕ1 ( x, λ1 ) = ϕ2 ( x, λ1 ) ≡ 0 bulunur. Bu ise λ1 ‘in (3.7) - (3.9)
sınır değer probleminin özdeğeri olması ile çelişir. O halde λ1 basit özdeğerdir.
18
Daha önce de bahsedildiği gibi (3.7) - (3.9) sınır değer probleminin
özdeğerleri ile
ϕ2 (π , λ ) cos β + ϕ1 (π , λ ) sin β = 0
denkleminin kökleri çakışmaktadır. Bu denklemde (3.23)’ten ϕ1 (π , λ ) ve ϕ2 (π , λ )
değerleri yerine yazılırsa
1
sin ( λπ −ν ) + O = 0
λ
(3.27)
elde edilir. Burada ν ’nün değeri (3.22)’den
π
ν = β −α −
1
{ p ( t ) + r ( t )} dt
2 ∫0
(3.28)
şeklinde bulunur. (3.27) denkleminden λ ’nın büyük değerlerinde
λnπ −ν = nπ + δ n ( n = 0, ±1, ±2,...)
olduğunu göstermek zor değildir.
Bu değerler (3.27)’de yerine yazılırsa
1
1
sin δ n = O yani δ n = O bulunur. Sonuç olarak
n
n
λn = n +
ν
1
+ O ( n = 0, ±1, ±2,...)
π
n
(3.29)
asimptotik formülü elde edilir.
(3.29) formülü kullanılarak,
ϕ1 ( x, λn ) = un ( x )
ve
ϕ2 ( x, λn ) = vn ( x )
yazılırsa
1
un ( x ) = cos (ξ n − α ) + O
n
(3.30)
1
vn ( x ) = sin (ξ n − α ) + O
n
(3.31)
asimptotik formülleri elde edilir. Burada
x
1
ξ n = ξ n ( x, λn ) = λn x − ∫ { p ( t ) + r ( t )} dt
20
dir.
19
4. BULGULAR VE TARTIŞMA
4.1. (1.1) - (1.4) SINIR DEĞER PROBLEMİNİN ÖZDEĞERLERİNİN
BAZI ÖZELLİKLERİ
Lemma 4.1.1. (1.1) - (1.4) sınır değer probleminin özdeğerleri reeldir.
İspat: Aksini varsayalım. λ0 , (1.1) - (1.4) sınır değer probleminin reel
olmayan bir özdeğeri,
(u ( x ) , w ( x ))
de bu özdeğere karşılık gelen özvektör
fonksiyonu olsun. Belirtelim ki, her bir x ∈ [ 0,1] için u ( x ) + w ( x ) > 0 ’dır.
(1.1) - (1.2) denklemlerine göre
d
u ( x ) w ( x ) − u ( x ) w ( x ) = λ0 − λ0
dx
{
} (
){ u ( x )
2
+ w( x)
2
}
(4.1)
eşitliği doğrudur. Gerçekten de (1.1) - (1.2) denklemlerine göre
d
u ( x ) w ( x ) − u ( x ) w ( x ) = u ′ ( x ) w ( x ) + u ( x ) w′ ( x ) − u ′ ( x ) w ( x ) − u ( x ) w′ ( x )
dx
{
}
2
{
2
}
{
}
2
= {λ0 + P ( x )} w ( x ) − λ0 + R ( x ) u ( x ) − λ0 + P ( x ) w ( x ) + {λ0 + R ( x )} u ( x )
(
= λ0 − λ0
){ u ( x )
2
+ w( x)
2
2
}
olur.
(4.1) özdeşliği x değişkenine göre 0’dan 1’e integre edilirse
{u (1) w (1) − u (1) w (1)} − {u ( 0 ) w ( 0 ) − u ( 0 ) w ( 0)}
(
= λ0 − λ0
1
) ∫{ u ( x)
2
+ w( x)
0
elde edilir.
2
}
(4.2)
dx
(1.5) koşuluna göre λ0 cos β + a = 0 olamaz.
λ0 cos β + a = 0 ’dır.
cos β ≠ 0 durumunda λ0 = −
özdeğerinin reel olmaması ile çelişir.
Varsayalım ki
a
elde edilir. Bu ise λ0
cos β
cos β = 0 durumunda ise a = 0 olur ve
σ = a sin β − b cos β = 0 elde edilir ki, bu da (1.5) koşulu ile çelişir. Demek ki
λ0 cos β + a ≠ 0 ’dır. Böylece (1.4) sınır koşulundan
20
u (1) =
λ0 sin β + b
w (1)
λ0 cos β + a
(4.3)
elde edilir. cos α = 0 olduğunda (1.3) koşuluna göre
w ( 0) = 0
olur. Sonuncuya ve (4.3)’e göre (4.2) eşitliği
(λ
0
)
− λ0 σ w (1)
λ0 cos β + a
2
1
(
= λ0 − λ0
2
) ∫{ u ( x)
2
+ w( x)
0
2
} dx
(4.4)
biçimini alır. λ0 reel olmadığından (4.4)
σ w (1)
2
λ0 cos β + a
1
2
{
2
= ∫ u ( x) + w( x)
0
2
} dx
1
biçiminde de yazılabilir.
Sonuncu eşitlik σ < 0 ve
∫{ u ( x)
(4.5)
2
+ w( x)
0
2
} dx > 0
eşitsizlikleri ile çelişir. Demek ki; cos α = 0 olduğunda λ0 reeldir.
cos α ≠ 0 olduğunda ise (1.3) göre u ( 0 ) = w ( 0 ) tan α olur. Sonuncuyu ve
(4.3)’ü (4.2)’de dikkate alırsak yine (4.5) çelişkisi elde edilir. Lemma 4.1.1 ispat
edildi.
Kolayca gösterilebilir ki (1.1) - (1.2) denklemler sisteminin
u ( 0, λ ) = sin α , w ( 0, λ ) = cos α
(4.6)
başlangıç koşullarını sağlayan tek türlü belirli ( u ( x, λ ) , w ( x, λ ) ) çözümü vardır.
Ayrıca her bir sabitlenmiş x ∈ [ 0,1] için u ( x, λ ) ve w ( x, λ ) fonksiyonları λ
argümentinin tam fonksiyonlarıdır. Bu hükmün ispatı [2, pp:14]’deki Teorem 1.1’in
ispatına benzer biçimde yapılır.
Belirtelim ki, (1.1) - (1.4) sınır değer probleminin özdeğerleri
( λ cos β + a ) u (1, λ ) − ( λ sin β + b ) w (1, λ ) = 0
(4.7)
denkleminin kökleridir.
Lemma 4.1.2. (1.1) - (1.4) sınır değer probleminin özdeğerleri en fazla
sayılabilir tanedir ve bu özdeğerlerin oluşturduğu küme sonlu limit noktasına sahip
değildir. Ayrıca (1.1) - (1.4) sınır değer probleminin tüm özdeğerleri basittir.
21
İspat: (1.1) - (1.4) sınır değer probleminin özdeğerleri (4.7) denkleminin sol
tarafındaki tam fonksiyonun sıfırlarıdır. Lemma 4.1.1’e göre λ parametresinin reel
olmayan değerlerinde bu fonksiyon sıfırdan farklıdır. Özdeş olarak sıfır olmayan
tam fonksiyonun sıfırları en fazla sayılabilir tanedir ve sonlu limit noktasına sahip
değildir.
Şimdi (1.1) - (1.4) sınır değer probleminin özdeğerlerinin basit olduğunu
ispatlayalım. Önce gösterelim ki;
d
{u ( x, λ ) w ( x, µ ) − u ( x, µ ) w ( x, λ )}
dx
= ( λ − µ ) {u ( x, λ ) u ( x, µ ) + w ( x, λ ) w ( x, µ )}
(4.8)
eşitliği doğrudur. Gerçekten de (1.1) - (1.2) denklemlerine göre
d
{u ( x, λ ) w ( x, µ ) − u ( x, µ ) w ( x, λ )}
dx
= {u ′ ( x, λ ) w ( x, µ ) + u ( x, λ ) w′ ( x, µ )} − {u ′ ( x, µ ) w ( x, λ ) + u ( x, µ ) w′ ( x, λ )}
{λ + P ( x )} w ( x, λ ) w ( x, µ ) − {µ + R ( x )} u ( x, λ ) u ( x, µ )
− {µ + P ( x )} w ( x, λ ) w ( x, µ ) + {λ + R ( x )} u ( x, λ ) u ( x, µ )
= ( λ − µ ) {u ( x, λ ) u ( x, µ ) + w ( x, λ ) w ( x, µ )}
elde edilir. (4.8)’in her iki tarafı 0’dan 1’e integre edilip (4.6) yerine yazılırsa
u (1, λ ) w (1, µ ) − u (1, µ ) w (1, λ )
(4.9)
1
= ( λ − µ ) ∫ {u ( x, λ ) u ( x, µ ) + w ( x, λ ) w ( x, µ )}dx
0
olur. λ ≠ µ kabul edelim. Bu durumda (4.9)’dan
u (1, λ ) w (1, µ ) − u (1, µ ) w (1, λ ) 1
= ∫ {u ( x, λ ) u ( x, µ ) + w ( x, λ ) w ( x, µ )}dx
λ−µ
0
elde edilir. Sonuncu eşitlikte µ → λ iken limite geçilirse,
w (1, λ )
∂u (1, λ )
∂w (1, λ ) 1
2
2
− u (1, λ )
= ∫ {u ( x, λ )} + {w ( x, λ )} dx
∂λ
∂λ
0
{
}
(4.10)
bulunur.
Gösterelim ki, (4.7) denkleminin yalnızca basit kökleri vardır.
Aksini
varsayalım. Yani λ = λ ∗ (4.7) denkleminin çok katlı kökü olsun. Bu durumda,
22
(λ
∗
cos β + a ) u (1, λ ∗ ) − ( λ ∗ sin β + b ) w (1, λ ∗ ) = 0 ,
u (1, λ ) cos β + ( λ cos β + a )
∗
∗
− w (1, λ ∗ ) sin β − ( λ ∗ sin β + b )
(4.11)
∂u (1, λ ∗ )
∂λ
∂w (1, λ ∗ )
∂λ
(4.12)
=0
olur.
İspatlayalım ki, λ ∗ cos β + a ve λ ∗ sin β + b sayıları aynı anda sıfır olamaz.
Yani λ ∗ cos β + a = 0 ve λ ∗ sin β + b = 0 olsun.
Aksini varsayalım.
cos β = 0
(veya sin β = 0 ) olduğunda a = 0 (uygun olarak b = 0 ) olur ve σ = 0 elde edilir.
Sonuncu ise (1.5) ile çelişir. cos β .sin β ≠ 0 durumunda ise λ ∗ = −
b
a
=−
sin β
cos β
yani, σ = a sin β − b cos β = 0 olur. Sonuncu yine (1.5) ile çelişir. Böylece
(λ
∗
2
2
cos β + a ) + ( λ ∗ sin β + b ) > 0
olur.
λ ∗ cos β + a ≠ 0 olsun. Bu durumda (4.11) ve (4.12)’den
u (1, λ ∗ ) =
∂u (1, λ ∗ )
∂λ
=
λ ∗ sin β + b
w (1, λ ∗ ) ,
λ ∗ cos β + a
σ w (1, λ ∗ )
(λ
∗
cos β + a )
2
∗
λ ∗ sin β + b ∂w (1, λ )
+ ∗
λ cos β + a ∂λ
elde edilir. Bu eşitlikler λ = λ ∗ için (4.10)’da yerine yazılırsa
{
}
σ w (1, λ * )
(λ
*
2
cos β + a )
1
2
{{
2
} {
} } dx
= ∫ u ( x, λ ∗ ) + w ( x , λ ∗ )
0
2
elde edilir. Bu ise σ < 0 olması ile çelişir. O halde (1.1) - (1.4) sınır değer
probleminin bütün özdeğerleri basittir.
λ ∗ sin β + b ≠ 0 durumu ise benzer biçimde yapılır.
23
4.2. BAZI YARDIMCI İDDİALAR
Pν ( x ) ve Rν ( x )
I.
(ν = 1, 2 ) , [ 0,1]
aralığında sürekli ve bu aralıkta
P2 ( x ) > P1 ( x ) > 0 , R2 ( x ) > R1 ( x ) > 0 koşullarını sağlayan fonksiyonlar olsun.
Aşağıdaki iki denklemler sistemini göz önüne alalım:
(ϕ ( x ) ,ψ ( x ) )
1
1
ϕ ′ − P ( x )ψ = 0,
1
1
1
ψ 1′ + R1 ( x ) ϕ1 = 0,
(4.13)
ϕ ′ − P ( x )ψ = 0,
2
2
2
ψ 2′ + R2 ( x ) ϕ2 = 0.
(4.14)
vektör
fonksiyonu
(4.13)
denklemler
sisteminin,
(ϕ ( x ) ,ψ ( x ) ) vektör fonksiyonu ise (4.14) denklemler sisteminin aşikardan farklı
2
2
çözümü olsun.
Aşağıdaki iki lemma [3, pp:152-153]’deki karşılaştırma teoremlerinden
kolayca elde edilir.
Lemma
4.2.1.
Eğer
ϕ1 ( 0 ) = 0
veya
ϕ1 ( 0 ) ≠ 0 ,
ϕ2 ( 0 ) ≠ 0 ,
ψ 1 ( 0) ψ 2 (0)
ise ( 0,1] yarı - açık aralığında ϕ2 ( x ) fonksiyonunun sıfırlarının
≥
ϕ1 ( 0 ) ϕ2 ( 0 )
sayısı, ϕ1 ( x )
fonksiyonunun sıfırlarının sayısından az değildir ve ϕ2 ( x )
fonksiyonunun k . sıfırı, ϕ1 ( x ) fonksiyonunun k . sıfırından küçüktür.
ψ 1 ( 0 ) = 0 veya ψ 1 ( 0 ) ≠ 0 , ψ 2 ( 0 ) ≠ 0 ,
aralığında ψ 2 ( x )
ϕ1 ( 0 ) ϕ 2 ( 0 )
≤
ise
ψ 1 (0) ψ 2 (0)
( 0,1]
fonksiyonunun sıfırlarının sayısı, ψ 1 ( x )
Eğer
yarı - açık
fonksiyonunun
sıfırlarının sayısından az değildir ve ψ 2 ( x ) fonksiyonunun k . sıfırı, ψ 1 ( x )
fonksiyonunun k . sıfırından küçüktür.
24
Lemma 4.2.2. Eğer ϕ1 ( x ) ve ϕ2 ( x ) fonksiyonlarının ( 0,1) aralığında
sıfırlarının sayısı eşit ve ϕ1 (1) ≠ 0, ϕ 2 (1) ≠ 0 ise
ψ 1 (1) ψ 2 (1)
>
eşitsizliği doğrudur.
ϕ1 (1) ϕ2 (1)
Eğer ψ 1 ( x ) ve ψ 2 ( x ) fonksiyonlarının ( 0,1) aralığında sıfırlarının sayısı eşit ve
ψ 1 (1) ≠ 0, ψ 2 (1) ≠ 0 ise
ϕ1 (1) ϕ2 (1)
eşitsizliği doğrudur.
<
ψ 1 (1) ψ 2 (1)
II. (ϕ ( x ) ,ψ ( x ) ) vektör fonksiyonu
ϕ ′ − p ( x )ψ = 0,
ψ ′ + r ( x ) ϕ = 0
denklemler sisteminin aşikardan farklı çözümü olsun. Burada p ( x ) , r ( x ) ∈ C [ 0,1]
ve p ( x ) > 0 , r ( x ) > 0 ( 0 ≤ x ≤ 1) ’dır.
x( 0 ) ( f ) (uygun olarak x(1) ( f ) ) ile f ( x ) ∈ C [ 0,1] fonksiyonunun [ 0,1)
yarı – açık aralığındaki en küçük (uygun olarak en büyük) sıfırını gösterelim.
Lemma 4.2.3 [28]. ϕ ( x ) (uygun olarak ψ ( x ) ) fonksiyonunun ardışık iki
sıfırı arasına ψ ( x ) (uygun olarak ϕ ( x ) ) fonksiyonunun tek bir sıfırı yerleşir.
Ayrıca x( 0) (ϕ ) (uygun olarak x( 0 ) (ψ ) ) var ve ϕ ( 0 )ψ ( 0 ) > 0 (uygun olarak
ϕ ( 0 )ψ ( 0 ) < 0 ) ise x( 0) (ψ ) (uygun olarak x( 0) (ϕ ) ) de vardır ve x( 0) (ψ ) < x( 0) (ϕ )
(uygun olarak x( 0) (ϕ ) < x ( 0 ) (ψ ) )’dir.
Benzer biçimde x(1) (ψ ) (uygun olarak
x(1) (ϕ ) ) var ve ϕ (1)ψ (1) > 0 (uygun olarak ϕ (1)ψ (1) < 0 ) ise x(1) (ϕ ) (uygun
olarak x(1) (ψ ) ) de vardır ve x(1) (ψ ) < x (1) (ϕ ) (uygun olarak x(1) (ϕ ) < x (1) (ψ ) )’dir.
f ( x ) ∈ C [ 0,1] fonksiyonunun [ 0,1) yarı – açık aralığındaki sıfırlarının
sayısı N ( f ) olsun. Bu fonksiyonun [ 0,1) yarı – açık aralığındaki sıfırlarını t j ( f )
( j = 1, 2,..., N ( f ) ) ile gösterelim:
0 ≤ t1 ( f ) < t2 ( f ) < ⋅⋅⋅ < t N ( f ) ( f ) < 1 .
25
Lemma 4.2.3’ten aşağıdaki sonuç direk elde edilir.
Sonuç 4.2.1 [28]. Aşağıdaki iddialar doğrudur.
1o ϕ ( 0 )ψ ( 0 ) > 0 ve ϕ (1)ψ (1) > 0 ise,
N (ϕ ) = N (ψ ) ve 0 < t1 (ψ ) < t1 (ϕ ) < ⋅⋅⋅ < t N (ψ ) (ψ ) < t N (ϕ ) (ϕ ) < 1 dir;
2o ϕ ( 0 )ψ ( 0 ) < 0 ve ϕ (1)ψ (1) < 0 ise,
N (ϕ ) = N (ψ ) ve 0 < t1 (ϕ ) < t1 (ψ ) < ⋅⋅⋅ < t N (ϕ ) (ϕ ) < t N (ψ ) (ψ ) < 1 dir;
3o ϕ ( 0 )ψ ( 0 ) > 0 ve ϕ (1)ψ (1) < 0 ise,
N (ψ ) = N (ϕ ) + 1 ve 0 < t1 (ψ ) < t1 (ϕ ) < ⋅⋅⋅ < t N (ϕ ) (ϕ ) < t N (ψ ) (ψ ) < 1 dir;
4o ϕ ( 0 )ψ ( 0 ) < 0 ve ϕ (1)ψ (1) > 0 ise,
N (ϕ ) = N (ψ ) + 1 ve 0 < t1 (ϕ ) < t1 (ψ ) < ⋅⋅⋅ < t N (ψ ) (ψ ) < t N (ϕ ) (ϕ ) < 1 dir;
5o ϕ ( 0 ) = 0 ve ϕ (1)ψ (1) < 0 ise,
N (ϕ ) = N (ψ ) ve 0 = t1 (ϕ ) < t1 (ψ ) < ⋅⋅⋅ < t N (ϕ ) (ϕ ) < t N (ψ ) (ψ ) < 1 dir;
6o ϕ ( 0 ) = 0 ve ϕ (1)ψ (1) > 0 ise,
N (ϕ ) = N (ψ ) + 1 ve 0 = t1 (ϕ ) < t1 (ψ ) < ⋅⋅⋅ < t N (ψ ) (ψ ) < t N (ϕ ) (ϕ ) < 1 dir;
7o ψ ( 0 ) = 0 ve ϕ (1)ψ (1) > 0 ise,
N (ϕ ) = N (ψ ) ve 0 = t1 (ψ ) < t1 (ϕ ) < ⋅⋅⋅ < t N (ψ ) (ψ ) < t N (ϕ ) (ϕ ) < 1 dir;
8o ψ ( 0 ) = 0 ve ϕ (1)ψ (1) < 0 ise,
N (ψ ) = N (ϕ ) + 1 ve 0 = t1 (ψ ) < t1 (ϕ ) < ⋅⋅⋅ < t N (ϕ ) (ϕ ) < t N (ψ ) (ψ ) < 1 dir.
26
4.3.
(1.1)
-
(1.4)
SINIR
DEĞER
PROBLEMİNİN
ÖZFONKSİYONLARININ SALINIM ÖZELLİKLERİ
( u ( x, λ ) , w ( x , λ ) )
vektör fonksiyonu (1.1) - (1.2) denklemler sisteminin
(4.6) başlangıç koşulunu sağlayan çözümü olsun.
G kümesini aşağıdaki gibi
tanımlayalım:
G = {µ : µ cos β + a = 0 ∨ µ sin β + b = 0} .
Kolayca gösterilebilir ki, G kümesi boş değildir ve en fazla iki elemana sahiptir.
Kabul edelim ki,
µ∗ = min G , µ ∗ = max G ,
{
}
M = max max P ( x ) , max R ( x ) ,
0 ≤ x ≤1
0 ≤ x ≤1
λ∗ = min {µ∗ , − M } , λ∗ = max {µ ∗ , M }
dir. Aşağıdaki sonuç Lemma 4.2.1’den direk elde edilir:
Sonuç 4.3.1.
sağlandığında
( 0,1]
λ ′′ > λ ′ > λ∗
veya
λ ′′ < λ ′ < λ∗
koşullarından biri
yarı – açık aralığında u ( x, λ ′′ ) (uygun olarak w ( x, λ ′′ ) )
fonksiyonunun sıfırlarının sayısı, u ( x, λ ′ ) (uygun olarak w ( x, λ ′) ) fonksiyonunun
sıfırlarının sayısından az değildir ve
u ( x, λ ′′ )
(uygun olarak
w ( x, λ ′′ ) )
fonksiyonunun k . sıfırı, u ( x, λ ′ ) (uygun olarak w ( x, λ ′) ) fonksiyonunun k .
sıfırından küçüktür.
Şimdi, 0 ≤ x ≤ 1 olmak üzere u ( x, λ ) = 0 (veya w ( x, λ ) = 0 ) denklemini
göz önüne alalım. Bu denklemin çözümlerinin λ ’ya bağlı olduğu açıktır.
Aşağıdaki iki iddiada λ ∉ λ∗ , λ∗ kabul edilecektir.
Lemma 4.3.1. Eğer x0 ∈ [ 0,1] sayısı u ( x, λ0 ) (uygun olarak w ( x, λ0 ) )
fonksiyonunun bir sıfırı ise yeteri kadar küçük herhangi ε > 0 sayısı için öyle bir
δ > 0 sayısı vardır ki λ − λ0 < δ koşulunun sağlandığı her bir λ için u ( x, λ )
27
(uygun olarak w ( x, λ ) ) fonksiyonunun x − x0 < ε açık aralığında tek bir sıfırı
vardır.
Bu iddianın ispatı [2, pp:30]’daki Lemma 3.1’in ispatının tamamıyla
aynısıdır.
Bu lemmadan aşağıdaki sonuç elde edilir:
Sonuç 4.3.2.
λ parametresi değiştiğinde u ( x, λ ) (veya w ( x, λ ) )
fonksiyonunun sıfır kazanması veya kaybetmesi yalnızca 0 ve 1 bitim noktalarından
bir sıfırın dâhil olması ile mümkündür.
(1.1) - (1.4) sınır değer probleminin sayılabilir sayıda özdeğerlerinin varlığı
aşağıdaki teoremde ifade edilmiştir.
∞
Teorem 4.3.1. (1.1) - (1.4) sınır değer probleminin sınırsız azalan {λ− n }n =1
∞
negatif özdeğerler dizisi ve sınırsız artan {λn }n =1 negatif olmayan özdeğerler dizisi
vardır:
⋅⋅⋅λ− n < λ− n +1 < ⋅⋅⋅ < λ−1 < λ1 < ⋅⋅⋅ < λn −1 < λn < ⋅⋅⋅
Buna ek olarak öyle n∗ , n∗ , k ∗ , k∗ ∈ ∪ {0} sayıları vardır ki λn ( n > n∗ )
özdeğerine karşılık gelen
(u ( x ) , w ( x ))
n
n
özvektör fonksiyonu ve λ− n ( n > n∗ )
özdeğerine karşılık gelen ( u− n ( x ) , w− n ( x ) ) özvektör fonksiyonu aşağıdaki salınım
özelliklerine sahiptir:
π
π
1o α ∈ − , 0 ve β ∈ 0, ise,
2
2
N ( un ) = N ( wn ) + 1 = n + k ∗ − n∗ , x( 0) ( un ) < x ( 0 ) ( wn ) dir;
π π
π
2o α ∈ − ∪ 0, ve β ∈ 0, ise,
2 2
2
N ( wn ) = N ( un ) = n + k ∗ − n∗ , x( 0) ( wn ) < x ( 0 ) ( un ) dir;
28
π
π π
3o α ∈ − , 0 ve β ∈ − , 0 ∪ ise,
2
2 2
N ( un ) = N ( wn ) = n + k ∗ − n∗ , x( 0) ( un ) < x( 0) ( wn ) dir;
π π
π π
4o α ∈ − ∪ 0, ve β ∈ − , 0 ∪ ise,
2 2
2 2
N ( wn ) = N ( un ) + 1 = n + k ∗ − n∗ + 1 , x( 0) ( wn ) < x ( 0 ) ( un ) dir;
π
π
5o α ∈ − , 0 ve β ∈ − , 0 ise,
2
2
N ( u− n ) = N ( w− n ) = n + k∗ − n∗ , x( 0) ( u− n ) < x( 0 ) ( w− n ) dir;
π π
π
6o α ∈ − ∪ 0, ve β ∈ − , 0 ise,
2 2
2
N ( w− n ) = N ( u− n ) + 1 = n + k∗ − n∗ + 1 , x( 0) ( w− n ) < x( 0) ( u− n ) dir;
π
π π
7o α ∈ − , 0 ve β ∈ − ∪ 0, ise,
2
2 2
N ( u− n ) = N ( w− n ) + 1 = n + k∗ − n∗ , x( 0) ( u− n ) < x( 0 ) ( w− n ) dir;
π π
π π
8o α ∈ − ∪ 0, ve β ∈ − ∪ 0, ise,
2 2
2 2
N ( w− n ) = N ( u− n ) = n + k∗ − n∗ , x( 0) ( w− n ) < x( 0) ( u− n ) dir.
İspat: Biz (1.1) - (1.4) sınır değer probleminin yalnızca negatif olmayan
özdeğerler dizisinin varlığını ve uygun ( un ( x ) , wn ( x ) ) özvektör fonksiyonlarının
salınım özelliklerini inceleyeceğiz.
Negatif özdeğerlerle ilgili olan iddialar
tamamıyla benzer bir yolla ispatlanır.
29
λ∗ bu bölümün başında tanımlanmış sayı olmak üzere λ ≥ λ ∗ = λ∗ + 1
olsun.
( u ( x, λ ) , w ( x , λ ) )
vektör fonksiyonu (1.1) - (1.2) denklemler sisteminin
(4.6) başlangıç koşulunu sağlayan çözümü olsun.
Sonuç 4.3.1’e göre u ( x, λ )
fonksiyonunun [ 0,1) yarı – açık aralığında sıfırlarının sayısı, λ parametresinin
azalmayan fonksiyonudur.
(ϕ ( x ) ,ψ ( x ) ) vektör fonksiyonu,
1
1
(4.15)
ϕ ′ − λ − M − ψ = 0,
2
ψ ′ + λ − M − ϕ = 0
2
(4.16)
ϕ ( 0, λ ) = sin α , ψ ( 0, λ ) = cos α
(4.17)
denklemler sisteminin
başlangıç koşulunu sağlayan çözümü olsun. Kolayca gösterilebilir ki,
1
ϕ ( x, λ ) = sin λ − M − x + α
2
dır.
λ → +∞ iken ϕ ( x, λ ) fonksiyonunun
[ 0,1)
yarı – açık aralığındaki
sıfırlarının sayısı sınırsız artar. (1.1), (1.2), (4.6) sınır değer problemini (4.15) (4.17) sınır değer problemi ile karşılaştıralım. Lemma 4.2.1’den λ → +∞ iken
u ( x, λ ) fonksiyonunun [ 0,1) yarı – açık aralığında sıfırlarının sayısının sonsuz
arttığı elde edilir.
λ ≥ λ ∗ koşulu sağlandığında
u ( x, λ ) = 0
denklemini göz önüne alalım.
Lemma 4.3.1’e göre bu denklemin kökleri λ
parametresinin sürekli fonksiyonudur.
Öte yandan Sonuç 4.3.1’e göre α ≠ 0
olduğunda λ artarken u ( x, λ ) fonksiyonunun her bir sıfırı sola hareket eder ve
x = 0 noktasından geçmez. Zira sıfırların sayısı azalmaz; α = 0 olduğunda ise her
bir λ ≥ λ ∗ için u ( 0, λ ) = 0 ’dır ve λ artarken u ( x, λ ) fonksiyonunun x = 0 ’dan
farklı her bir sıfırı sola hareket eder fakat x = 0 noktasından yine geçemez. Zira bu
30
durumda da sıfırların sayısı azalmaz. Sonuç 4.3.2’ye göre sıfırlar yalnızca x = 1
noktasından dahil olabilirler.
λ = λ 0 sayısı λ ≥ λ ∗ ve u (1, λ ) = 0 koşullarını sağlayan ilk sayı, yani
λ 0 = min {λ : λ ≥ λ ∗ ∧ u (1, λ ) = 0} olsun. Açıktır ki,
böyle bir değer vardır.
(
)
Kabul edelim ki, u x, λ 0 fonksiyonunun [ 0,1) yarı – açık aralığında k ∗
tane sıfırı vardır.
λ = λ 1 sayısı λ > λ 0 ve u (1, λ ) = 0 koşullarını sağlayan ilk sayı, yani
{
}
(
)
λ 1 = min λ : λ > λ 0 ∧ u (1, λ ) = 0 olsun. u x, λ 1 fonksiyonunun [ 0,1) yarı – açık
aralığında k ∗ + 1 tane sıfırının olduğu açıktır. Bu yöntemle aşağıdaki özelliğe sahip
λ 0 , λ 1 , λ 2 ,... dizisini elde ederiz: λ k −1 < λ ≤ λ k olduğunda u ( x, λ ) fonksiyonunun
[ 0,1)
(
yarı – açık aralığında tam k ∗ + k
)
u 1, λ k = 0 ’dır. Kolayca görülür ki, λ k
tane sıfırı vardır ve ek olarak
( k = 0,1, 2,...)
sayıları (1.1) - (1.4) sınır
değer probleminin özdeğerleri değildir.
Lemma 4.2.2’ye göre
w (1, λ )
fonksiyonu
u (1, λ )
( λ
k −1
, λ k
)
aralığında kesin
azalandır. Öte yandan
(
) (
)
u x, λ k −1 = u x, λ k = 0
olduğundan
w (1, λ )
fonksiyonu λ k −1 , λ k
u (1, λ )
(
)
aralığında +∞ ’dan −∞ ’a kadar kesin
azalır.
T (λ ) =
λ cos β + a
σ
olsun. T ′ ( λ ) = −
ve σ < 0 olduğundan
2
λ sin β + b
( λ sin β + b )
T ( λ ) fonksiyonu λ sin β + b ≠ 0 koşulunun sağlandığı her bir aralıkta kesin
artandır.
31
n∗ sayısı (1.1) - (1.4) sınır değer probleminin 0, λ 0 aralığında yerleşen
w (1, λ )
fonksiyonu
u (1, λ )
özdeğerlerinin sayısı olsun.
( λ
k −1
, λ k
)
aralığında +∞ ’dan
−∞ ’a kesin azalan olduğundan
w (1, λ )
= T (λ )
u (1, λ )
(
denkleminin λ k −1 , λ k
)
aralığında tek bir çözümü vardır. Bu çözümü λn∗ + k ile
(
)
gösterelim: λn∗ + k ∈ λ k −1 , λ k . λ = λn∗ + k değerinin (1.4) koşulunu sağladığı açıktır.
Demek ki λn∗ + k , (1.1) - (1.4) sınır değer probleminin özdeğeridir ve ona karşılık
((
) (
gelen u x, λn∗ + k , w x, λn∗ + k
)) özvektör fonksiyonunun birinci komponentinin [0,1)
(
yarı – açık aralığındaki sıfırlarının sayısı u x, λ k
)
fonksiyonunun bu aralıktaki
sıfırlarının sayısı ile aynıdır. Yani k + k ∗ ’a eşittir.
4.4. θ n ( x ) FONKSİYONUNUN TANIMI VE ÖZELLİKLERİ
n∗ sayısı Teorem 4.3.1’in ispatında tanımlanmış negatif olmayan tamsayı
olmak üzere, bu bölüm boyunca n > n∗ kabul edeceğiz.
(u ( x ) , w ( x )) ,
n
n
(1.1) - (1.4) sınır değer probleminin λn özdeğerine
karşılık gelen özvektör fonksiyonu olsun.
θ n ( x ) = Arctan
un ( x )
olarak tanımlayalım. Daha kesin olarak
wn ( x )
θ n ( x ) = arg {wn ( x ) + iun ( x )}
(4.18)
yazabiliriz. (1.3) koşuluna göre θ n ( x ) fonksiyonu başlangıç değerini
θn ( 0) = α +
1 − l0
π
2
olarak alır. Burada
32
(4.19)
π
1, α ∈ 0, 2
l0 =
−1, α ∈ − π , 0
2
(4.20)
dır.
x değişkeninin diğer değerlerinde θ n ( x ) fonksiyonu 2kπ
( k ∈ )
kesinlik ile (4.18)’in yardımı ile verilir. Zira un ( x ) ve wn ( x ) fonksiyonları aynı
noktada sıfır olamaz.
θ n ( x ) fonksiyonu (4.19) koşulunu sağlayacak ve x
değişkenine göre sürekli olacak şekilde tek değerli olarak seçilebilir.
Lemma 4.4.1 [28]. θ n ( x ) fonksiyonu
θ n′ ( x ) = λn + P ( x ) cos 2 θ n ( x ) + R ( x ) sin 2 θ n ( x )
diferansiyel denklemini sağlar ve buna göre [ 0,1] aralığında kesin artandır.
(4.18) formülü gereğince un ( x ) fonksiyonunun sıfırları öyle noktalardır ki
bu noktalarda θ n ( x ) fonksiyonu π ’nin katlarına eşit değerler alır.
0 < θ n ( 0 ) ≤ π ve θ n ( x ) fonksiyonu artan olduğundan x ; 0’dan 1’e
değiştiğinde bu fonksiyon sonlu sayıda π , 2π ,... değerlerini alır.
xn,k
( k = 1, 2,...kn )
ile un ( x ) fonksiyonunun [ 0,1) yarı – açık aralığındaki
sıfırlarını gösterelim:
0 ≤ xn ,1 < xn ,2 < ⋅⋅⋅ < xn ,kn < 1 .
Salınım özellikleri hakkındaki Teorem 4.3.1’e göre n > n∗ olduğunda,
kn = n + k ∗ − n∗ olur. Böylece
θ n ( xn,k ) = kπ ( k = 1, 2,...kn ) ,
θ n (1) = arctan
λn sin β + b 1 − l1
+
π,
λn cos β + a
2
π
1, β ∈ 0, 2
l1 =
−1, β ∈ − π , 0 ∪ π
2 2
33
(4.21)
(4.22)
(4.23)
olur.
Lemma 4.4.2 [28].
xn,0 = 0 ve xn ,kn +1 = 1 olmak üzere, aşağıdaki
asimptotik formüller doğrudur:
λn = nπ + O (1) , ∆xn,k = xn,k +1 − xn ,k = O ( n −1 ) ( k = 0,1,...kn )
Lemma 4.4.3 [28].
w∗f (δ ) , f ( x ) fonksiyonunun
[ 0,1]
(4.24)
aralığındaki
süreklilik modülü ve w f (δ ) = δ + w∗f (δ ) olmak üzere her bir f ( x ) ∈ C [ 0,1]
fonksiyonu için
1
∫ f ( x ) cos 2θ ( x ) dx = O ( w ( n ) )
−1
n
f
0
formülü doğrudur.
4.5. (1.1) - (1.4) SINIR DEĞER PROBLEMİNİN ÖZDEĞERLERİ VE
ÖZVEKTÖR FONKSİYONLARI İÇİN ASİMPTOTİK FORMÜLLER
Bu bölüm boyunca n sayısının mutlak değer olarak yeterince büyük bir
tamsayı olduğunu kabul edeceğiz.
(Φ ( x ) , Ψ ( x )) ,
n
n
(1.1) - (1.4) sınır değer probleminin bir özvektör
fonksiyonu ve Φ n ( x ) , [ 0,1) yarı – açık aralığında n sayıda sıfıra sahip olsun. µn
ile
(Φ ( x ) , Ψ ( x ))
n
n
özvektör fonksiyonuna karşılık gelen özdeğeri gösterelim.
Salınım özellikleri ile ilgili Teorem 4.3.1’den n > 0 ise µn = λn − k ∗ + n∗ ve n < 0 ise
µn = λn− k + n ’dır.
∗
∗
Teorem 4.5.1. Aşağıdaki asimptotik formüller doğrudur.
µ n = nπ + β − α −
π
2
( sgn β + sgn ( −α ) )
1
−
1
P ( x ) + R ( x ) ) dx + O w ( n −1 )
(
∫
20
(
34
)
(4.25)
( n > 0) ,
µn = ( n + 1) π + β − α +
π
π
π
sgn − β − + sgn α −
2
2
2
1
1
−1
− ∫ ( P ( x ) + R ( x ) ) dx + O w n
20
( ( )) ( n < 0) ,
( ),
Ψ ( x ) = cos (ξ ( x ) + α ) + O ( n ) .
Φ n ( x ) = sin (ξ n ( x ) + α ) + O n
n
(4.26)
−1
(4.27)
−1
(4.28)
n
Burada t ≥ 0 için sgn t = 1 , t < 0 için sgn t = −1 ’dir. w (δ ) = δ + w1 (δ ) ve
w1 (δ )
[ 0,1]
P ( x ) − R ( x ) fonksiyonunun
aralığındaki süreklilik modülüdür.
Ayrıca
x
ξ n ( x ) = λn x −
1
( P ( t ) + R ( t ) ) dt
2 ∫0
(4.29)
dir.
İspat:
Önce
(4.25)’i
ispatlayalım.
θ n ( x ) = arg ( Ψ n ( x ) + iΦ n ( x ) )
fonksiyonunu ele alalım. Lemma 4.4.1’den θ n ( x ) fonksiyonu
θ ′ ( x ) = µ n +
1
1
P ( x ) + R ( x ) ) + ( P ( x ) − R ( x ) ) cos 2θ n ( x )
(
2
2
(4.30)
diferansiyel denklemini sağlar ve buna göre [ 0,1] aralığında kesin artandır. θ n ( 0 )
ve θ n (1) , (4.19) ve (4.22)’de verildiği gibidir ve λn ile kn yerine sırasıyla µn ile n
yazılır.
Kolayca gösterilebilir ki,
θ n ( 0 ) = α +
π
2
+
π
2
sgn ( −α )
(4.31)
π π
θ n (1) = nπ + β + − sgn β + O ( n −1 )
2 2
(4.30) özdeşliğinin her iki tarafını 0’dan 1’e integre edip (4.31) değerlerini yerine
yazarsak
nπ + β − α −
π
2
( sgn β + sgn ( −α ) ) + O ( n )
−1
35
1
= µn +
1
1
1
P ( x ) + R ( x ) ) dx + ∫ ( P ( x ) − R ( x ) ) cos 2θ n ( x ) dx
(
∫
20
20
elde ederiz. Buradan
µ n = nπ + β − α −
1
−
π
2
( sgn β + sgn ( −α ) )
1
1
1
P ( x ) + R ( x ) ) dx − ∫ ( P ( x ) − R ( x ) ) cos 2θ n ( x ) dx + O ( n −1 )
(
∫
20
20
1
bulunur.
1
Lemma 4.4.3’ten
P ( x ) + R ( x ) ) dx = O w ( n −1 )
(
∫
20
(
)
(
(
)
değerlendirmesi
)
yerine yazılırsa O w ( n −1 ) + O ( n −1 ) = O w ( n −1 ) olduğundan
µ n = nπ + β − α −
π
2
( sgn β + sgn ( −α ) ) −
1
1
( P ( x ) + R ( x ) ) dx + O w ( n−1 )
2 ∫0
(
)
elde edilir. (4.25) ispat edildi.
Şimdi (4.26)’yı ispatlayalım. n < 0 kabul edelim ve aşağıdaki problemi
inceleyelim. (1.1) - (1.4) sınır değer probleminde λ spektral parametresi yerine
µ = −δ alalım ve µ < 0 olduğunda negatif özdeğerler için asimptotik formüller elde
edelim. µ < 0 olduğundan δ > 0 olur. P1 ( x ) = − R ( x ) , R1 ( x ) = − P ( x ) , a1 = −b ,
b1 = − a , a1∗ = b , b1∗ = a , U ( x ) = w ( x ) ve W ( x ) = u ( x ) yazalım.
1o 0 ≤ α ≤
π
2
, 0≤β ≤
π
2
olsun.
O halde (1.1) - (1.4) sınır değer problemi
U ′ − {δ + P1 ( x )}W = 0 ,
(4.32)
W ′ + {δ + R1 ( x )}U = 0 ,
(4.33)
π
π
U ( 0 ) cos − α − W ( 0 ) sin − α = 0 ,
2
2
(4.34)
π
π
δ cos 2 − β + a1 U (1) − δ sin 2 − β + b1 W (1) = 0
(4.35)
sınır değer problemine dönüşür ve
π
π
− β − b1 cos − β = a sin β − b cos β = σ < 0
2
2
σ ∗ = a1 sin
36
yine sağlanır. δ > 0 olduğundan (4.25)’e göre
π
π
π
δ − n = −nπ + α − β − sgn − β + sgn α −
2
2
2
1
+
1
( P ( x ) + R ( x ) ) dx + O w n−1
2 ∫0
( ( ))
elde edilir. Buradan
µn = −δ − n = nπ + β − α +
π
π
π
sgn − β + sgn α −
2
2
2
1
1
− ∫ ( P ( x ) + R ( x ) ) dx + O w n −1
20
(4.36)
( ( ))
bulunur.
2o −
π
2
≤α < 0, 0 ≤ β ≤
π
2
olsun.
O halde (1.1) - (1.4) sınır değer problemi (4.32) - (4.33) denklemleri ile
π
π
U ( 0 ) cos −α − − W ( 0 ) sin −α − = 0
2
2
(4.37)
ve (4.35) sınır koşulları ile verilmiş sınır değer problemine dönüşür. (4.25)’e göre
π
π
π
δ − n = −nπ + π + α − β − sgn − β + sgn α +
2
2
2
1
+
1
P ( x ) + R ( x ) ) dx + O w n −1
(
∫
20
( ( ))
elde edilir. Buradan
µn = −δ − n = nπ − π + β − α +
π
π
π
sgn − β + sgn α +
2
2
2
1
1
− ∫ ( P ( x ) + R ( x ) ) dx + O w n −1
20
(4.38)
( ( ))
bulunur.
3o 0 ≤ α ≤
π
2
,−
π
2
≤ β < 0 olsun.
O halde (1.1) - (1.4) sınır değer problemi (4.32) - (4.33) denklemleri ile (4.34) ve
37
π ∗
π ∗
δ cos − β − 2 + a1 U (1) − δ sin − β − 2 + b1 W (1) = 0
(4.39)
sınır koşulları ile verilmiş sınır değer problemine dönüşür. Burada
σ ∗∗ = a1∗ sin − β −
π
π
∗
− b1 cos − β − = a sin β − b cos β = σ < 0
2
2
yine sağlanır. (4.25)’e göre
π
π
π
δ − n = −nπ − π + α − β − sgn − β − + sgn α −
2
2
2
1
+
1
( P ( x ) + R ( x ) ) dx + O w n−1
2 ∫0
( ( ))
elde edilir. Buradan
µn = −δ − n = nπ + π + β − α +
π
π
π
sgn − β − + sgn α −
2
2
2
1
1
− ∫ ( P ( x ) + R ( x ) ) dx + O w n −1
20
(4.40)
( ( ))
bulunur.
4o −
π
2
≤α < 0, −
π
2
≤ β < 0 olsun.
O halde (1.1) - (1.4) sınır değer problemi (4.32) - (4.33) - (4.37) - (4.39) sınır değer
problemine dönüşür. (4.25)’e göre
π
π
π
δ − n = −nπ + α − β − sgn − β − + sgn α +
2
2
2
1
+
1
( P ( x ) + R ( x ) ) dx + O w n−1
2 ∫0
( ( ))
elde edilir. Buradan
µn = −δ − n = nπ + β − α +
π
π
π
sgn − β − + sgn α +
2
2
2
1
1
− ∫ ( P ( x ) + R ( x ) ) dx + O w n −1
20
(4.41)
( ( ))
bulunur. Sonuç olarak (4.36) - (4.38) - (4.40) - (4.41) asimptotik formülleri (4.26)
da verilen
38
µn = ( n + 1) π + β − α +
π
π
π
sgn − β − + sgn α −
2
2
2
1
−
1
−1
P ( x ) + R ( x ) ) dx + O w n
(
∫
20
şeklinde genel biçimde yazılabilir.
( ( ))
(4.26)’nın ispatı bitti.
(4.27) ve (4.28)
asimptotik formüllerinin hesaplanması tamamıyla [2, pp:52-57]’deki gibidir.
39
5. SONUÇLAR VE ÖNERİLER
Bu tezde ele alınan sonuçlar, Bulgular ve Tartışma bölümünde
4.1 (1.1) - (1.4) Sınır Değer Probleminin Özdeğerlerinin Bazı Özellikleri,
4.2 Bazı Yardımcı İddialar,
4.3 (1.1) - (1.4) Sınır Değer Probleminin Özfonksiyonlarının Salınım Özellikleri,
4.4 θ n ( x ) Fonksiyonunun Tanımı ve Özellikleri,
4.5 (1.1) - (1.4) Sınır Değer Probleminin Özdeğerleri ve Özvektör Fonksiyonları için
Asimptotik Formüller,
başlıkları altında toplanmıştır.
4.1’de
u '− {λ + P ( x )} w = 0 ,
w '+ {λ + R ( x )} u = 0 ,
u ( 0 ) cos α − w ( 0 ) sin α = 0 ,
( λ cos β + a ) u (1) − ( λ sin β + b ) w (1) = 0
sınır değer problemi ele alındı ve σ = a sin β − b cos β < 0 durumda bu problemin
özdeğerlerinin:
1. Reel olduğu,
2. Basit olduğu,
3. En fazla sayılabilir bir küme oluşturduğu ve bu kümenin sonlu limit
noktasının bulunmadığı ispatlandı.
4.2’de
ϕ ′ − P ( x )ψ = 0,
1
1
1
ψ 1′ + R1 ( x ) ϕ1 = 0
ve
ϕ ′ − P ( x )ψ = 0,
2
2
2
ψ 2′ + R2 ( x ) ϕ 2 = 0
40
şeklinde iki denklemler sistemi ele alındı ve P2 ( x ) > P1 ( x ) > 0 , R2 ( x ) > R1 ( x ) > 0
( x ∈ [0,1])
durumunda çözüm fonksiyonlarının birinci ve ikinci komponentlerinin
sıfırlarının dizilişi hakkında bir takım sonuçlar elde edildi.
Ayrıca bu kısımda,
ϕ ′ − p ( x )ψ = 0,
ψ ′ + r ( x ) ϕ = 0
şeklinde verilen denklemler sisteminin çözüm fonksiyonlarının birinci ve ikinci
komponentlerinin sıfırlarının birbirine göre durumları, 0 ve 1 bitim noktalarındaki
işaretlerinin davranışlarına göre belirlendi.
4.2’de elde edilen bu sonuçlar (1.1) - (1.4) sınır değer probleminin
özvektör fonksiyonlarının komponentlerinin salınım özelliklerinin incelenmesinde
büyük rol oynamaktadır.
4.3’de (1.1) - (1.4) sınır değer probleminin sonsuz sayıda negatif
özdeğerinin ve sonsuz sayıda negatif olmayan özdeğerinin varlığı ispat edildi.
Bununla beraber α ve β sayılarının durumuna göre (1.1) - (1.4) sınır değer
probleminin özvektör fonksiyonlarının komponentlerinin salınım özellikleri
incelendi.
4.4’de θ n ( x ) fonksiyonunun tanımı ve bazı özellikleri verildi ve bundan
yararlanılarak (1.1) - (1.4) sınır değer probleminin özdeğerleri ve özvektör
fonksiyonlarının komponentlerinin sıfırları arasındaki farklar için asimptotik
değerlendirmeler yapıldı. Ayrıca bu kısımda (1.1) - (1.4) sınır değer probleminin
özdeğerlerinin süreklilik modülüne bağlı asimptotik formüllerinin verilebileceği
ispatlandı. Bu kısımda elde edilen sonuçlar (1.1) - (1.4) sınır değer probleminin
özdeğerleri ve özvektör fonksiyonlarının komponentleri için asimptotik formüllerin
elde edilmesinde büyük rol oynamaktadır.
4.5’te (1.1) - (1.4) sınır değer probleminin özdeğerleri ve özvektör
fonksiyonlarının komponentleri için asimptotik formüller elde edildi.
41
Bu tez çalışmasında, araştırmanın amacında belirtilen ana hedeflere
ulaşılmıştır. (1.1) - (1.4) sınır değer probleminin spektral özelliklerinin incelenmesi
bazı problemleri de yanında getirmiştir. Bu problemler aşağıdaki gibi sıralanabilir:
a) (1.1)
-
(1.4)
sınır
değer
probleminin
spektral
özellikleri
σ = a sin β − b cos β < 0 koşulu dahilinde incelenmiştir. σ > 0 durumunda
da (1.1) - (1.4) sınır değer probleminin özdeğerleri reel ve basit olur mu?
b) (1.1) - (1.4) sınır değer probleminin farklı fonksiyonel uzaylarda tabanlığı ile
ilgili hangi sonuçları elde etmek mümkündür?
Tezde incelenmiş problemlerin doğal sonucu olarak bu iki problemin de
araştırılması önerilir.
42
KAYNAKLAR
[1]
Naimark, M.A. “Linear Differential Operators” 2nd ed., Nauka, Moskow,
(1969) (in Russian); English Trans. of 1st ed., Parts I,II, Ungar, New York,
(1967), (1968).
[2]
Levitan, B.M. and Sargsyan, I.S. “An Introduction to Spectral Theory.
Selfadjoint Ordinary Differential Operators” (in Russian), Nauka, Moscow
(1970); Amer. Math. Soc. (1975) (Translated from Russian).
[3]
Kamke E.W.H. “Differentialgleichungen”, (in German) Leipzig (1959),
Translated
under
the
title
“Spravochnik
po
obyknovennym
differentsial'nym uravneniyam”, Moskow, (1981)
[4]
Walter, J. “Regular Eigenvalue Problems with Eigenvalue Parameter in the
Boundary Condition.” Mathematische Zeitschrift, 133 (4): 301-312, (1973)
[5]
Fulton, C.T. “Two Point Boundary Value Problems with Eigenvalue
Parameter
Contained
in
the
Boundary
Conditions”,
Proc.Roy.Soc.Endinburg Sect.A, 77: 293-308, (1977)
[6]
Scheneider, A. “A Note on Eigenvalue Problems with Eigenvalue
Parameter in the Boundary Conditions”, Mathematische Zeitschrift, 136
(2): 163-167, (1974)
[7]
Hinton, D.B. “An Expansion Theorem for an Eigenvalue Problem with
Eigenvalue Parameter in the Baundary Condition”, Quart.J.Math. Oxford,
30 (2): 33-42, (1979)
[8]
Russakovskii, E.M. “Operator Treatment of Boundary Problems with
Spectral Parameters Entering Via Polynomials in the Boundary
Conditions”, Functional Analysis and Its Applications, 9 (4): 358-359,
(1975)
[9]
Shkalikov, A.A. “Boundary Value Problems for Ordinary Differential
Equations with a Parameter in the Boundary Conditions”, Functional
Analysis and Its Applications, 16 (4): 324-326, (1982)
[10] Shkalikov, A.A. “Boundary Value Problems for Ordinary Differential
Equations with a Parameter in the Boundary Conditions”, Trudy Seminara
im. Petrovskogo, (9): 190-229, (1983)
43
[11] Makhmudov, A. P. “Basics of Non-linear Spectral Analysis”, Dokl. Akad
Nauk SSSR., 277 (6): 1318-1323, (1984)
[12] Meleshko, S.V. and Pokornyi, Yu. V. “On a Vibrational Boundary Value
Problem”, Differentsial’nye Uravneniya, 23 (8): 1466-1467, (1987)
[13] Kerimov, N.B. and Allakhverdiyev, T.I. “On a Baundary Value Problem I”
Differentsial’nye Uravneniya, 29 (1): 54-60, (1993) (in Russian), Trans. in
Differential Equations, 29 (1): 45-50, (1993)
[14] Kerimov, N.B. and Allakhverdiyev, T.I. “On a Baundary Value Problem
II” Differentsial’nye Uravneniya, 29 (6): 952-960, (1993) (in Russian),
Trans. in Differential Equations, 29 (6): 814-821 (1993)
[15] Binding, P.A., Browne, P.J. and Seddighi, K. “Sturm-Liouville Problems
with Eigenparameter Depent Boundary Conditions”, Proc. Edinburgh
Math. Soc. (2),37 (1): 57-72 (1993)
[16] Binding, P.A. and Browne, P.J. “Oscillation Theory for Indefinite SturmLiouville
Problems
with
Eigenparameter-Dependent
Boundary
Conditions”, Proceedings of the Royal Society of Edinburgh 127 (6):
1123-1136 (1997)
[17] Kerimov, N. B. and Mamedov, Kh. R. “On One Boundary Value Problem
with a Spectral Parameter in the Boundary Conditions”, Siberian
Mathematical Journal 40 (2): 281-290 (1999)
[18] Kerimov, N.B. and Poladov, R.G. “On Basisity in Lp ( 0,1) (1 < p < ∞ ) of
the System of Eigenfunctions of One Boundary Value Problem I” Proc. of
Institue of Math. and Mech. of NAS of Azerbaijan 22: 53-64 (2005)
[19] Kerimov, N.B. and Poladov, R.G. “On Basisity in Lp ( 0,1) (1 < p < ∞ ) of
the System of Eigenfunctions of One Boundary Value Problem II” Proc. of
Institue of Math. and Mech. of NAS of Azerbaijan 23: 65-76 (2005)
[20] Kerimov, N. B. and Aliev, Z. S. "Basis Properties of a Spectral Problem
with Spectral Parameter in the Boundary Condition" Sbornik: Mathematics
197 (10): 1467-1487 (2006)
[21] Kerimov, N. B. and Aliev, Z. S. “On the Basis Property of the System of
Eigenfunctions of a Spectral Problem with Spectral Parameter in the
Boundary Condition” Differential Equations 43 (7): 905-915 (2007)
44
[22] Kerimov, N.B. and Mirzoev, V.S. “On the Basis Properties of One
Spectral Problem with a Spectral Parameter in Boundary Conditions”
Sibirsk. Math. Zh. 44: 1041-1045 (2003) (in Russian), English Trans.
Siberian Math. J. 44: 813-816. (2003)
[23] Kapustin, N.Yu. and Moiseev, E.I. “A Remark on the Convergence
Problem for Spectral Expansions Corresponding to a Classical Problem
with Spectral Parameter in the Boundary Condition” Differential
Equations 37 (12): 1677-1683 (2001)
[24] Kapustin, N.Yu. and Moiseev, E.I. “The Basis Property in Lp of the
Systems of Eigenfunctions Corresponding to Two Problems with a
Spectral Parameter in the Boundary Condition” Differential Equations 36
(10): 1498-1501 (2000)
[25] Kapustin, N.Yu. and Moiseev, E.I. “Convergence of Spectral Expansions
for Functions of the Hölder Class for Two Problems with a Spectral
Parameter in the Boundary Condition” Differential Equations 36 (8): 11821188 (2000)
[26] Kapustin, N.Yu. “On a Spectral Problem Arising in a Mathematical Model
of Torsional Vibrations of a Rod with Pulleys at the Ends” Differential
Equations 41 (10): 1490-1492 (2005)
[27] Kapustin, N.Yu. “An a Priori Estimate for the Solution of a Mixed
Problem for the Heat Equation” Differential Equations 42 (10): 1447-1452
(2006)
[28] Kerimov, N.B. “A Boundary Value Problem for the Dirac System with a
Spectral Parameter in the Boundary Conditions” Differential Equations 38
(2): 164-174 (2002) Translated from Differentsial’nye Uravneniya 38 (2):
155-164 (2002)
[29] Balcı, M. “Matematik Analiz” Ertem Matbaası, 124-138 (1984)
[30] Thomas, G.B. and Finney, R.L. “Calculus and Analytic Geometry”
Addison-Wesley Publishing Company, (1984)
[31] Shevchuk, I.A. “Approximation by Polinomials and Trace of Functions
Continuous on a Segment” Naukova Dymka, Kiev (1992)
45
[32] Ahlfors L.V. “Complex Analysis” McGraw-Hill Book Company (Third
Edition), Singapore (1979)
46
ÖZGEÇMİŞ
1984 yılında Mersin’de doğdum. İlk ve orta öğrenimimi bu şehirde yaptım.
2002-2006 yılları arasında Mersin Üniversitesi Matematik Bölümünde lisans
öğrenimimi tamamladım. 2006 yılında Mersin Üniversitesi Fen Bilimleri Enstitüsü
Matematik Anabilim Dalında yüksek lisans programına başladım. 25 Aralık 2006
tarihinden bu yana Mersin Üniversitesi Fen Bilimleri Enstitüsü kadrosuna bağlı
olarak Matematik Anabilim Dalında Araştırma Görevlisi olarak görev yapmaktayım.
47