deney-4-kondansatör

KONDANSATÖRÜN DOLMA VE BOŞALMA EĞRİSİ,
ZAMAN SABİTİ KAVRAMI
Hazırlayan:
Arş.Gör. Koray GÜRKAN
[email protected]
KONDANSATÖR
Klasik olarak bildiğiniz gibi, iki iletken paralel plaka arasına dielektrik (yalıtkan) bir madde
konulursa kondansatör oluşur. Kondansatörler bu yalıtkan maddenin türüne göre oldukça
çeşitlidir.
Kondansatörü oluşturan bu iki iletken plaka arasına sabit bir V gerilimi uygulanırsa oluşan
elektrik alan sonucu kondansatör plakasındaki elektronlar kaynağın pozitif tarafına doğru çekilir.
Elektronların bu alanı dengelemek amacıyla çekilmesi yük akışıdır. Belirli bir süre sonra iki
plaka arasında alanı dengeleyen Q yükü birikir. Biriken Q yükünün uygulanan V gerilimine oranı
kondansatörün “sığası” ya da “kapasitesi” olarak adlandırılır, C ile gösterilir, birimi “Farad”
dır..
C=Q/V
Q: Biriken yük miktarı
V: Uygulanan gerilim
C: Sığa ya da kapasite
(Coulomb)
(Volt)
(Farad)
1
Bu kapasite hesaplanmak istenirse aşağıdaki eşitlik kullanılır.
C  ε r .ε o .
o
r
A
d
A
d
: Boşluğun dielektrik katsayısı:
8.854x10-12 F/m
: Plakalar arasında kullanılan yalıtkan malzemenin bağıl (relative) dielektrik katsayısı
(oran olduğu için birimsizdir)
: Plakaların alanı
[m]
: Plakalar arası uzaklık
[m]
KONDANSATÖRÜN DOLMASI
Aşağıdaki devre kondansatörün dolması ve boşalması sırasındaki gerilim değişiminin analizi için
kullanılacaktır. Anahtar ”1” konumundayken kondansatör E gerilim kaynağı tarafından R
direncinin ve kondansatörün C sığasının belirleyeceği hızla dolar.
Anahtarın ”1” konumu için şu eşitlikler yazılabilir.
E  VR (t)  VC (t)
E  I R (t).R  VC (t)
Seri bağlı olduklarından IR(t) = IC(t)’dir.
E  I C (t).R  VC (t)
2
Kondansatörün akım-gerilim ilişkisi gereğince I C (t)  C
E  R.C.
dVC (t)
dt
dVC (t)
 VC (t)
dt
diferansiyel denklemi Vc(0)=0 başlangıç koşuluyla çözülürse
VC (t)  E(1  e

t
RC
)  E(1  e

t
τ
)
(1)
şeklindeki, kondansatör geriliminin zamanla değişimini gösteren ifadeye ulaşılır.
t = 0 için
t   için
VC(0) = 0 ve
VC() = E
olur. Yani başlangıçta boş olan (uçları arasında potansiyel fark bulunmayan) ideal kondansatör,
potansiyel fark sonucu akan akımla yavaş yavaş dolar (şarj olur) ve belirli bir süre sonra
kondansatör gerilimi E değerine ulaşacağından akım akmaz, kondansatör gerilimi bu değerde
sabitlenir. R.C çarpımı devrenin
„Zaman Sabiti“ (Time Constant) olarak adlandırılır ve
(Okunuşu: „To“) ile gösterilir. Birimi „saniye“ dir.
(1) ifadesinde t =  için,
VC(t) = E.( 1 – e -/) = E.( 1 – e -1 ) = E.( 1 – 0,368 ) = (0,632).E
(2)
bulunur. Yani, kondansatör boşken devreye bağlanırsa  saniye sonra kondansatör üzerindeki
gerilim E değerinin 0.632’sine ulaşmış olacaktır. Yaklaşık 5 saniye sonunda kondansatörün
dolmuş olduğu söylenebilir.
3
10
9
Kondansator Gerilimi (V)
8
7
6
5
4
3
2
1
0
0
10
20
30
40
50
60
70
80
90
100
Zaman (s)
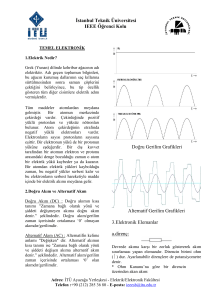
Şekil 1: Kondansatörün dolma eğrisi
E=10 V, R=10 k ve C=1000 F için kondansatörün gerilim değişimi (ya da dolma eğrisi) Şekil
1’de verilmiştir. Bu değerler için zaman sabiti hesaplanırsa,
 = R.C = (10.103).(1000.10-6) = 10 s
bulunur. Eğriye dikkat edilirse 10 s sonra kondansatör gerilimi 6.32 V’a ulaşmıştır. 50 saniye
sonra kondansatörün 10 V’a ulaştığı söylenebilir.
Kondansatörün gerilim değişimini bildiğimize göre akım değişimini de bulabiliriz. Kondansatör
geriliminin üstel artması sonucu, bir ucu DC gerilim kaynağına diğer ucu kondansatöre bağlı
bulunan R direncinin üzerindeki gerilim de üstel olarak azalır. Bu fark direnç üzerinden geçen
akımı ve dolayısıyla seri bağlı olduklarından kondansatörü dolduran akımı oluşturur. Bu nedenle
devreden geçen akım, R direnci uçlarındaki potansiyel farkın maksimum olduğu ilk anda en
büyük değerini alacak kondansatörün dolmasıyla üstel olarak azalarak sıfıra doğru azalacaktır.
Matematiksel olarak ise akan akım kondansatör geriliminin zamana göre türevinin C ile
çarpımıdır.
Dolayısıyla genel olarak,
Vc(t) = E ( 1 – e-t/) ise,
t
t
t

dVC (t)
d
C.E  τ
E 
I C (t)  C
 C. (E(1  e τ )) 
e  e R.C
dt
dt
τ
R
Ifadesi akım değişimini verecektir. İfadeye dikkat edilirse;
4
t = 0 için
IC(0) = E/R
olmaktadır. İlk başta kondansatör gerilimi sıfır olduğundan direnç doğrudan toprağa bağlıymış
gibi düşünebilirsiniz. Daha sonra, artan kondansatör gerilimiyle akım azalır ve
t   için IC() = 0
olur. Yani kondansatör dolduğundan artık içerisinden akım akmaz.
-3
KONDANSATOR AKIMI (A)
1
x 10
0.8
0.6
0.4
0.2
0
0
10
20
30
40
50
60
Zaman (s)
70
80
90
100
Şekil 2 : Kondansatör dolması sırasında akan akımın zamanla değişimi
KONDANSATÖRÜN BOŞALMASI
Şimdi, daha önce E gerilimine kadar dolmuş olan kondansatörü anahtarı „2“ konumuna alarak R
direnci üzerinden boşaltalım. Daha önceki elektrik alan sonucu kondansatörün üst tarafında
birikmiş olan yükler R direncinin kondansatör plakaları arasında köprü olmasıyla iki tarafta
dengelenir ve kondansatör boşalmış olur.
5
Bu defa R direnci üzerindeki gerilim ile C kondansatörü üzerindeki gerilim birbirini izleyerek
azalacaktır. VC’nin değişimi;
VC (t)  E.e

t
RC
 E.e

t

olacaktır.
Eşitliği kontrol etmek gerekirse, E gerilimine kadar dolmuş olan kondansatörün boşalması için
anahtarın „2“ konumuna alındığı ana t=0 dersek
t=0
t
için
için
Vc(0) = E.e-0 = E
Vc() = E.e- = 0
olur.
Kondansator Gerilimi (V)
10
8
6
4
2
0
0
10
20
30
40
50
60
Zaman (s)
70
80
90
100
R direnci üzerinden akan akım ise VC=VR geriliminin R değerine bölünmüşü olacaktır.
t
t
E  RC
E 
I R (t) 
.e

.e
R
R
6
-3
1
x 10
AKIM (A)
0.8
0.6
0.4
0.2
0
0
10
20
30
40
50
60
Zaman (s)
70
80
90
DENEY
Deney için gerekli malzemeler
9 V Pil
Pil bağlantısı için kablo
7
10 k direnç
100
1000 F kondansatör ( >10 V)
Elektriksel bağlantılar için breadboard
Sayısal Multimetre
Geçen zamanın ölçümü için saat
8
DENEYIN YAPILIŞI
3- Şekildeki bağlantıyı yaptığınız
anda kronometreyi başlatarak her 5
saniyede bir kondansatör gerilimini
kaydediniz.
1- Pil gerilimini ölçünüz.
E = ......................... V
Zaman (s)
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
90
100
2 – Multimetrenin ölçüm uçlarını şekilde
gibi değiştiriniz. Gerilimi okuyunuz.
VC(0) = ........................... V
9
Gerilim (V)
SORULAR
1- Elde ettiğiniz ölçüm sonuçlarıyla
dolma ve boşalma sırasındaki
kondansatör geriliminin zamanla
değişimini
çizdiriniz.
Devrenin
zaman sabitini grafikten bulunuz.
2- Eğri
uydurma
yöntemiyle,
çizdirdiğiniz
grafiklerin
matematiksel ifadesini elde ediniz.
3- Eleman toleransları aşağıdadır.
R = 10 k +/- % 5
4- Kronometreyi
sıfırladıktan
sonra
bağlantıyı şekildeki gibi değiştirerek
hemen ardından kronometreyi tekrar
başlatınız. Kondansatör gerilimini yine
5’er saniye aralıklarla ölçünüz.
Zaman (s)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
90
100
C = 1000 F +/- % 20
Buna göre devrenin zaman sabiti hangi
değerler arasında ölçülebilir?
Gerilim (V)
Sorularınız için:
[email protected]
10