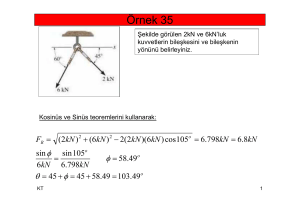
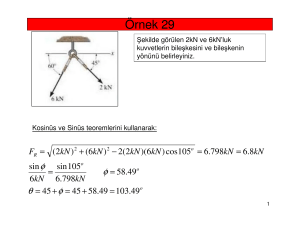
x - Ahi Evran Üniversitesi

T.C.
AHİ EVRAN ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
BİR STURM-LIOUVILLE PROBLEMİNİN BAZI
ÖZELLİKLERİ VE GREEN FONKSİYONU
Yasemin KUZU
YÜKSEK LİSANS TEZİ
MATEMATİK ANABİLİM DALI
KIRŞEHİR
HAZİRAN 2012
T.C.
AHİ EVRAN ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
BİR STURM-LIOUVILLE PROBLEMİNİN BAZI
ÖZELLİKLERİ VE GREEN FONKSİYONU
Yasemin KUZU
YÜKSEK LİSANS TEZİ
MATEMATİK ANABİLİM DALI
DANIŞMAN:
Prof. Dr. Mahir KADAKAL
KIRŞEHİR
HAZİRAN 2012
ONAY
Fen Bilimleri Enstitüsü Müdürlüğü’ne
Bu çalışma jürimiz tarafından Matematik Anabilim Dalında YÜKSEK LİSANS
TEZİ olarak kabul edilmiştir.
Başkan
Prof. Dr. Mahir KADAKAL
Üye
Yrd. Doç. Dr. İ. Onur KIYMAZ
Üye
Yrd. Doç. Dr. Muharrem AKTÜMEN
Onay
Yukarıdaki imzaların, adı geçen öğretim üyelerine ait olduğunu onaylarım.
…/06/2012
Enstitü Müdürü
Doç. Dr. Mahmut YILMAZ
i
ÖZET
Bu çalışmada, sınır şartlarında özdeğer parametresi bulunduran SturmLiouville problemi incelenmiştir.
Beş bölümden oluşan bu çalışmanın “Giriş” bölümünde, Sturm-Liouville
denklemi, matematiksel fizik, Sturm and Liouville ile ilgili bilgiler verilmiştir.
“Literatür özeti” bölümünde özdeğer parametresi içeren lineer diferansiyel
denklemler için sınır değer problemlerinin genel tarihine ve diğer çalışmalardan elde
edilmiş sonuçların kısa bir özetine değinilmiştir.
“Genel Bilgiler” bölümünde tez konumuzla ilgili olan genel bilgilere ve
tanımlara yer verilmiştir.
“Bulgular ve Tartışma” bölümünde Sturm-Liouville probleminin özdeğerleri
incelenmiş, asimptotik ifadeler ve Green Fonksiyonu bulunmuştur.
Çalışmamızın sonuncu bölümü olan “Sonuç ve Öneriler” bölümünde ise
araştırmamızdan elde edilen sonuçlara ve bu sonuçların önemine yer verilmiştir.
Anahtar Kelimeler: Sınır değer problemi,
Sturm-Liouville teorisi,
diferansiyel operatör, özdeğer, özfonksiyon, asimptotik davranış, Green Fonksiyonu
ii
ABSTRACT
In this study we have examined Sturm-Liouville Problem which has
eigenvalue parameter in the boundary conditions.
This study has arranged in 5 chapters, in “The Introduction” chapter,
informations related to Sturm-Liouville equation, mathematical physics, Sturm and
Liouville has been given.
In “The Literatur” chapter, we have mentioned the general history of
boundary value problems for linear differential equations which has eigenvalue
parameter and a brief summary of the results obtained from other studies.
In “The General Knowledge” chapter, we have mentioned the general
knowledge and definitions about the subject of our thesis.
In “Finding and Discussion” chapter, we have examined eigenvalue of
Sturm-Liouville Problem and obtained asymptotic formulas and Green’s function.
In “Conclusions and Recommendations” chapter, we have mentioned
possible solutions obtained from the study and important of these solutions.
Key Words: Boundary value problem, Sturm-Liouville Theory, Differential
operator, eigenvalue, eigenfunction, asymptotic behavior, Green’s Function.
iii
TEŞEKKÜR
Yüksek lisans öğrenimim boyunca olduğu gibi tez çalışmamın da her
aşamasında her türlü desteğini ve emeğini esirgemeyen; kıymetli zamanını, fikirlerini
ve bilgilerini benimle paylaşan; gösterdiği sonsuz anlayış ve ilgiyle tezimin ortaya
çıkmasına yardımcı olan saygıdeğer danışman hocam Prof. Dr. Mahir KADAKAL’ a
minnettarlığımı sunarım.
Yüksek lisans öğrenimim boyunca maddi ve manevi desteklerini benden
hiçbir zaman esirgemeyen bölümümüzün değerli hocalarına şükranlarımı sunarım.
Öğrenim hayatım boyunca olduğu gibi bu çalışma dönemimde de hep
yanımda olan kıymetli anne ve babama, beni bu tarz çalışmalara teşvik eden değerli
kardeşlerime ve sonsuz desteklerini benden hiçbir zaman esirgemeyen sevgili eşime
teşekkür ederim.
iv
İÇİNDEKİLER DİZİNİ
ONAY…………………………………………………………………………………………………...i
ÖZET.......................................................................................................................................................ii
ABSTRACT…………………………………………………………………………………………...iii
TEŞEKKÜR…………………………………………………………………………………………...iv
İÇİNDEKİLER DİZİNİ………………………………………………………………………………v
SİMGELER VE KISALTMALAR………………………………………………………………….vi
1. GİRİŞ………………………………………………………………………………………………...1
2. LİTERATÜR ÖZETİ………………………………………………………………………………5
3. GENEL BİLGİLER………………………………………………………………………………..9
3.1. Lineer Operatörler……………………………………………………………………………….9
3.2. Lineer Diferansiyel İfade ve Sınır Şartları…………………………………………………......10
3.3. Diferansiyel Operatörlerin Özdeğerleri ve Özfonksiyonları………………………..………….11
3.4. Metrik Uzayları…………………………………………………………………………………11
3.5. Normlu Uzaylar ve Banach Uzayları……………………………………………………………11
3.6. İç Çarpım Uzayları ve Hilbert Uzayları………………………………………………………...12
3.7. Hilbert Uzayında Simetrik Operatörler........................................................................................13
3.8. L2  a, b  Uzayı ve Sobolev Uzayı………………………………………………………………13
3.9. Kompleks Fonksiyonların Sıfır Yerlerinin Sayısı........................................................................14
3.10. Mutlak ve Düzgün Yakınsaklık………………………………………………………….…….14
3.11. SDP’nin Çözümünün Varlığı, Tekliği ve Parametreye Göre Tamlık Teoremi...........................17
3.12. Asimptotik Davranışlar………………………………………………………………………...17
3.13. Sturm-Liouville Problemleri…………………………………………………………………..19
3.14.İkinci Mertebeden Lineer Diferansiyel Denklemler İçin Paramatrelerin Değişimi Yöntemi…. 22
3.15.Green Fonksiyonu………………………………………………………………………………24
4. MATERYAL VE METOD……………………………………………………………………….26
5. BULGULAR VE TARTIŞMA…………………………………………………………………...27
5.1. Sınır Değer Probleminin İfadesi..................................................................................................27
5.2. Sınır Değer Problemi ile Aynı Özdeğere Sahip Olan Lineer Operatörün Kurulması................. 27
5.3. SDP ile İlgili Yardımcı BDP’lerinin Çözümleri ve Özdeğer Parametresine Göre Analitikliği... 32
5.4. Temel Çözümler ve Karakteristik Fonksiyon…………………………………………………..40
5.5.   x  ve    x  Çözüm Fonksiyonlarının Asimptotiği……………………………………...44
5.6.   x  ve    x  Fonksiyonlarının Wronskianının Asimptotiği...............................................56
5.7. Green Fonksiyonunun Kurulması.................................................................................................58
5.8. Özdeğerler İçin Asimptotik Formlar.............................................................................................61
6. SONUÇLAR VE ÖNERİLER………………………………………………………………… 70
KAYNAKLAR……………………………………………………………………………………....71
ÖZGEÇMİŞ………………………………………………………………………………………….74
v
SİMGELER VE KISALTMALAR
E   E, K , , 
: Lineer veya Vektör uzayı
X   X,d
: Metrik uzay
 E,  
: Lineer normlu uzay
: x ve y elemanlarının iç çarpımı
x, y
E   E, , 

: İç çarpım uzayı
L2  a, b
: Karesi integrallenebilen fonksiyonlar uzayı
W  f , g
: Wronskian determinantı

: Özdeğer
q  x
: Potansiyel fonksiyonu
H
: Hilbert Uzayı
C  a, b 
:  a, b aralığında tanımlı ve sürekli olan fonksiyonların lineer
uzayı
W22  0,  
: Sobolev Uzayı
O, o,
: Asimptotik davranışları tarif etmek için kullanılan simgeler
SDP
: Sınır Değer Problemi
BDP
: Başlangıç Değer Problemi
vi
1. GİRİŞ
Isının bir nesne üzerinde, belli bir konumda ve zamanda, nasıl dağılacağını
tanımlayan parçalı diferansiyel denkleme ısı denklemi denir. Kartezyen koordinat
sisteminde, ( x, y, z ) konumu ve t zamanı göstermek üzere, ısı denkleminin genel
ifadesi
  2u  2u  2u 
u
k 2  2  2   0
t
z 
 x y
şeklindedir. Burada k bir sabit ve u  u( x, y, z, t ) dir. Isı denklemi bir boyutta ise
u
 2u
k 2  0
t
x
şeklindedir.
Matematik fiziğin birçok problemlerinin çözümünde en etkili ve klasik
yöntemlerden biri, Fourier yöntemidir. Değişkenlerine ayırma yöntemi de denilen bu
yöntemin uygulanması sonucunda, birçok problem, adi diferansiyel denklemler için
sınır değer problemine dönüştürülür. Ancak, Fourier yönteminin esaslandırılması için
elde edilen sınır değer probleminin, özfonksiyonlarının baz oluşturması veya hiç
olmazsa, özfonksiyonların ve bu fonksiyonlara bağlanmış fonksiyonların tam olması
gösterilmelidir. Bu ise, Lineer Diferansiyel operatörlerin spektral teorisinin başlıca
konusudur.
Matematik fizikte biliniyor ki, u  x, t  fonksiyonu
ut   2uxx ,
0 x ,
t 0
(1.1)
denklemini sağlar. Burada  , telin yapıldığı maddeye uygun fiziksel sabittir.
( 2 
K
; K -dahili ısı iletme katsayısı,  - yoğunluk, c - ısı tutumudur.)
c
Başlangıç anında telin her noktasındaki ısının değeri f  x  ile gösterilirse,
u  x,0   f  x  ,
0 x
(1.2)
başlangıç şartını almış oluruz. (1.1) denkleminin
u  0, t   0,
u  , t   0,
t 0
(1.3)
çözümünü bulacağız. Fourier yöntemine göre (1.1) denkleminin herhangi çözümünü
1
u  x, t   X  x  T  t 
(1.4)
şeklinde arayalım. (1.4)’ ü (1.1) de yerine yazarsak,
ut  XT ,
ux  TX ,
uxx  TX 
olduğundan
XT    2 X T
(1.5)
X  1 T 

X 2 T
(1.6)
elde edilir. (1.5) denklemini
şeklinde yazarak değişkenlerine ayırmış oluruz. Sol taraf sadece x değişkenine, sağ
taraf ise sadece t değişkenine bağlı olduğundan, (1.6) eşitliğinin her iki tarafı x ’e
ve t ’ye bağlı olmayan herhangi  sabitine eşittir (Bu sabite, ayırma sabiti denir.).
X  1 T 


X 2 T
Böylece
X  x
ve
T t 
fonksiyonları için iki adi diferansiyel denklem elde
edilmiş olur.
X    X  0
T    2T  0
(1.7)
(1.3) sınır şartları ise (1.4) denkleminden yararlanılarak
u  x, t   X  x  T  t 
u  0, t   X  0 T  t   0  X  0  T  t   X  0   0
ve
u  , t   X   T t   0  X   T t   X 
0
şekline dönüşür. Böylece X  x  fonksiyonu için
X    X
X  0  X 
(1.8)
0
(1.9)
sınır değer problemi elde edilmiş olur. Şimdi elde edilen bu sınır değer problemini
çözelim. Kolaylık olması için    2 ile gösterelim. O halde (1.8) denklemi
X    2 X  0
2
(1.10)
şeklinde yazılır.   0 olduğunda bu denklemin genel çözümü X  x   k1 x  k2
şeklindedir. (1.9) sınır şartlarında yerine yazarsak k1  k2  0 , yani u  x, t   0
trivial (aşikar) çözümü elde edildiğinden   0 hali incelenmelidir. O halde (1.10)
denkleminin genel çözümü;
X  x   k1ei x  k2ei x  k1 cos  x  k2 sin  x
(1.11)
şeklinde olur. (1.9) sınır şartlarında yerine yazarsak X  0   0 için
X  0  k1 cos  0  k2 sin  0
bulunur. Benzer şekilde X 
X
0

k1  0
için
  k1 cos 
 k2 sin 
 k2 sin   0
olur. k2  0 için (1.11) denklemi
X  x   0cos  x  0sin  x  0
olduğu görülür. Bu ise bizi u  x, t   0 aşikar çözüme götürür.
O halde
k2  0, sin   0 durumu incelenmelidir.
X
0
iken sin   0 ifadesinden n 
n
,
n  1, 2,... olduğu
görülür.    2 olduğundan
 n 



2
  
elde edilir. Bu sayılara (1.8), (1.9) sınır değer probleminin özdeğerleri denir. Bu
değerlere uygun gelen çözümler ise
X n  x   sin
n x
n  1, 2, ...
,
fonksiyonlarıdır ve bunların keyfi sabitle çarpımlarıdır. Bu fonksiyonlara ise (1.8),
(1.9) sınır değer problemlerinin özfonksiyonları denir. (1.7)’nin çözümleri ise
 n 

 t


2
Tn  t   e
şeklinde bulunur. O halde
 n 

 t


2
U n  x, t   e
3
sin
n x
fonksiyonu (1.1) denklemini ve (1.3) sınır şartlarını sağlar. Bu durumda (1.2)
başlangıç şartı
n x
f n  x   sin
(1.12)
şartına dönüşür. O halde f  x  , (1.12) şeklinde değilse (1.1), (1.3) sınır değer
probleminin (1.12) şeklinde çözümü bulunmaz. (1.1) denklemi ve (1.3) sınır şartları
homojen olduklarından
m
m
u  x, t    un  x, t Cnn   e
n 1
 n 




sin
n x
n 1
Cn
şeklindeki lineer birleşimlerde (1.1) denklemini ve (1.3) sınır şartlarını sağlar. (1.2)
başlangıç şartını sağlaması için f  x  fonksiyonu
m
f  x    sin
n 1
n x
Cn
(1.13)
şeklinde olmalıdır. (1.13) şartı ise (1.1) ve (1.3) problemi için hem fiziksel, hem de
matematiksel açıdan çok ağır olan sınırlayıcı şarttır. Bunu aradan kaldırabilmek için

f  x    X n  x Cn
n 1
serisine açıldığını kabul edelim. Bu halde belli şartlar altında


u  x, t    un  x, t  Cn   e
n 1
 n 

 t


n 1
2
sin
n x
Cn
fonksiyonu (1.1), (1.3) probleminin çözümü oluyor.
Yukarıdaki örnekte görüldüğü gibi birçok matematiksel fizik probleminin
çözümü uygun özdeğer probleminin özdeğer ve özfonksiyonları kullanılarak inşa
edilebilir.
4
2. LİTERATÜR ÖZETİ
Son yıllarda oldukça çok önem arz eden ve üzerine bir çok çalışma yapılan
Sturm-Liouville problemleri ilk olarak 19. yüzyılın ortalarında araştırılmaya
başlanmıştır. C. Sturm ve J. Liouville isimli iki bilim adamı ısı iletimi problemini
Fourier yöntemi ile araştırdıklarında karşılarına özdeğer parametresi içeren adi
diferansiyel denklemin bazı sınır şartlarını sağlayan çözümlerinin araştırılması
problemi çıkmıştır. Adi diferansiyel denklemler için sınır değer probleminin genel
hali
( y,  )  y ( n)  p1 ( x,  ) y ( n1)  ...  pn ( x,  ) y  0
n 1

V j ( y,  )   a jK    y 
K 0
K
 0   b jK y  K  1   0,
j  1, 2,..., n
(2.1)
(2.2)
biçiminde ifade edilebilir. Burada
ps  x,     ps  x    , pss  x   const ,
s  1,..., n
0
pmn  0, a jk    , b jk    fonksiyonları ise  nın polinomlarıdır.
(2.1), (2.2) tipinde problemlerin araştırılması G.D.Birkoff’un [3] ve [4]
çalışmalarıyla başlamıştır. G.D.Birkhoff’ın bu çalışmalarında özdeğer parametresine
bağlı lineer diferansiyel operatörler için temel çözüm sistemini oluşturan çözümlerin
asimptotik davranışları incelenmiş ve bazı asimptotik eşitlikler bulunmuştur. Ayrıca
G.D.Birkhoff’un bu çalışmalarında adi diferansiyel operatörler için regular sınır
şartları kavramı tanımlanmış ve uygun sınır değer probleminin kök fonksiyonlarının
(yani, özfonksiyonlarının ve şerik fonksiyonlarının (eigen functions and associated
functions)) tamlığı hakkında teorem ispatlanmıştır.
Bu tip problemler ilerleyen yıllarda, J.D.Tamarkin’in [22] çalışmasında (2.1)
denkleminin temel çözüm sistemini oluşturan fonksiyonların asimptotik davranışları
incelenmiş regular ve güçlü reguler sınır değer problemi kavramı tanımlanmıştır.
Güçlü regular sınır değer probleminin özdeğerleri için asimptotik formüller
bulunmuştur. Regular problemler için ise Green fonksiyonu değerlendirilmiştir ve
kök fonksiyonları üzerine açılım teoremleri ispatlanmıştır. Daha sonraki yıllarda bu
ve benzer problemler birçok matematikçi tarafından yoğun şekilde araştırılmıştır.
5
Son yıllarda adi diferansiyel operatörler teorisi ile ilgili farklı problemler de
yoğun bir biçimde incelenmiş ve sadece denklemde değil, sınır şartlarında da
özdeğer parametresi bulunduran Sturm-Liouville tipinde problemler özel ilgi
çekmeye başlamıştır. Bu konuda çok sayıda çalışma yapılmış, makale ve kitaplar
yazılmıştır.
Bu konudaki önemli çalışmalar hakkında [7], [8], [9], [14], [15], [17], [18],
[21], [25], [28], [30] kaynaklarında yeteri kadar bilgi verilmiştir.
İkinci mertebeden adi diferansiyel denklemler için bazı kendine eşlenik sınır
değer problemleri [2], [10], [11], [12], [19], [20], [27], [29] çalışmalarında
incelenmiştir. Örneğin;
J. Walter’ın [27] çalışmasında


1
  pu   qu  u,
r
x   a1 , a2 
(2.3)
  11u  a1   12u  a1     11u  a1   12u  a1  
(2.4)
  21u  a2   22u  a2      21u  a2    22u  a2  
(2.5)
biçiminde Sturm-Liouville problemi için yeni bir  ölçümü tanımlanmış (problemin
katsayı fonksiyonları olan p  x  ve r  x  fonksiyonlarından bağımlı olan ölçüm) ve
uygun
L2   a, b ;  
Hilbert
A : L2   a, b ;    L2   a, b ;  
uzayında
(2.3)-(2.5)
problemine
uygun
operatörü tanımlayarak (2.3)-(2.5) probleminin
operatör-teorik yorumlamasını vermiştir. Daha sonra A operatörünün kendine
eşlenikliğini ispatlayarak, kendine eşlenik operatörlerin fonksiyonel analizinden
bilinen özelliklerinden yararlanmakla açılım teoremi ispatlanmıştır.
Schneider’in [20] çalışmasında ise
  pu   qu   ru
u a  0
  1u  b   2u  b     1u  b    2u  b  
sınır şartlarının sadece bir tanesinde özdeğer parametresi içeren uygun problem için
S-hermityen sınır değer problemleri yöntemiyle araştırılabileceğini göstermiş ve
özfonksiyonlar sistemi üzerine açılımın düzgün ve mutlak yakınsaklığı için yeter
şartlar bulmuştur.
6
Fulton’un [8] çalışmasında,
 : u  qu  u
cos  u  a   sin  u  a   0

  1u  b    2u  b     1u  b    2u  b 

şeklinde bir problem ele almış ve problemde sadece fonksiyonel analizin
yöntemlerini değil, Titcmarsh’ın [25] çalışmasının klasik yöntemlerinden de
faydalanarak özdeğer parametresinin sınır şartlarından sadece bir tanesinde
bulunduğu durum için çalışmalar yapmıştır. Çalışmalarında uygun problem için
özdeğer ve özfonksiyonların asimptotiğini bulmuş ve farklı açılım teoremleri
ispatlanmıştır.
Russakovskiy’nin [19] çalışmasında, sınır şartları polinom biçiminde özdeğer
parametresi içeren problemlerin operatör-teorik yorumunu vermiştir.
Kerimov ve Mamedov’un [12] çalışmasında
u  q  x  u   2u,
0  x 1
(2.6)
0
 1   2 2  u  0   u  0   0
(2.7)
0
 1  2 2  u 1  u 1  0
(2.8)


problemine uygun
A   2  B     C    0
biçiminde operatörler demetini kurarak (2.6)-(2.8) problemine farklı bir yaklaşımla
operatör-teorik yorum getirmişlerdir. Bu çalışmada özdeğer ve özfonksiyonların
asimptotik davranışları incelenmiş ve ayrıca özfonksiyonların sıfır yerleri hakkında
klasik sorulara benzer sonuçlar bulmuşlardır.
Tez çalışmamızda ise sınır şartlarında özdeğer parametresi bulunduran SturmLiouville tipindeki bir probleminin özdeğerleri ve özfonksiyonları incelenmiştir.
7
3. GENEL BİLGİLER
Bu bölümde tez çalışmamızda yararlandığımız temel kavram ve sonuçlar
hakkında kısa ve öz bilgilere yer verilmiştir.
3.1. Lineer Operatörler
E kümesi ve bu kümenin elemanları arasında aşağıdaki şartları sağlayan “  ”
işlemi   : E  E  tanımlansın;
1. x  y  y  x
2.
(Değişme özelliği)
 x  y  z  x   y  z
(Birleşme özelliği)
3. "  " ile gösterilen ve x  E için x    x şartını sağlayan bir tek
 E elemanı mevcuttur.
4. Her x  E için  x ile gösterilen ve x    x  şartını sağlayan bir tek
 x  E elemanı mevcuttur. Yani her x  E için x  y  0 olacak şekilde
bir tek y  E vardır. Bu durumda y elemanı  x ile gösterilir.
Ayrıca bir K cismi (genel olarak K 
veya
olarak düşünülür, sayı cismi
olarak da adlandırılır) için K ile E nin elemanları arasında “  ” ile gösterilen
 : K  E  E işlemi tanımlansın ve bu işlem için aşağıdaki özellikler sağlansın;
5.    x     x
(  ,   K ve x  E için)
6.   x  y    x   y
7.
    x   x   x
8. 1 x  x
(“1” K cisminin birim elemanı)
Bu şartları (aksiyomları) sağlayan E   E, K , ,  kümesi K cismi üzerinde
lineer veya vektör uzay olarak adlandırılır. Kısaca E lineer uzaydır denir.
E lineer uzayının herhangi D alt kümesinin elemanları E lineer uzayında
tanımlı “  ” ve “  ” işlemlerine göre bir lineer uzay oluşturuyorsa, D ’ye E lineer
uzayının lineer alt uzayı denir.
E lineer uzayı, bu uzayın bir D lineer alt uzayı ve bir A : D  E dönüşümü
verilsin. Eğer her x, y  D ve her   K için
8
A  x  y   Ax  Ay,
A   x    Ax
şartları sağlanıyorsa, A dönüşümü lineer operatör olarak adlandırılır. D ’ye A lineer
operatörünün tanım bölgesi denir [17].
3.2. Lineer Diferansiyel İfade ve Sınır Şartları
pi ( x) :

(i  0,1, 2,..., n), sürekli fonksiyonlar olmak üzere
( y) : p0 ( x) y ( n)  p1 ( x) y ( n1)  ...  pn ( x) y,
x  (a, b)
biçiminde ifadeye n  mertebeden lineer diferansiyel ifade denir. Genel olarak her x
için p0 ( x)  0 olduğu kabul edilir.
U ( y) : 0 y(a)  1 y(a)  ...  an1 y ( n1) (a)+0 y(b)  1 y(b)  ...  n1 y ( n1) (b)
biçimindeki ifadeye ise sınır değer ifadesi denir. Ui ( y), i  1, 2,..., m ifadeleri sınır
değer ifadeleri olduğunda
Ui ( y)  0,
i  1, 2,..., m
biçimindeki eşitlikler sınır şartları olarak adlandırılır.
Bilindiği gibi C  a, b ile,
 a, b 
aralığında tanımlı ve sürekli olan
fonksiyonların lineer uzayı gösterilir.
 f  C a, b

f , f ,..., f ( n )  C  a, b
lineer uzayı ise C ( n )  a, b biçiminde gösterilir.
L : C  a, b  C  a, b


D( L)  D  y  C  a, b y  C ( n )  a, b ,U i ( y )  0, i  1, 2,..., m
L( y)  ( y)  p0 ( x) y
( n)
 p1 ( x) y
( n 1)
 ...  pn ( x) y
eşitlikleri ile tanımlanan L  lineer operatörüne lineer diferansiyel operatör veya
( y ) diferansiyel ifadesi ile Ui ( y)  0, i  1, 2,..., m sınır şartlarının ürettiği lineer
diferansiyel operatör denir [17].
9
3.3. Diferansiyel Operatörlerin Özdeğerleri ve Özfonksiyonları
E lineer uzayında tanım bölgesi D  A olan A : E  E lineer operatörü
verilsin. Eğer herhangi   0 ve herhangi u0  H , u0  0 için
Au0  0u0
eşitliği sağlanırsa, 0 sayısına A operatörünün özdeğeri, u0  H , u0  0 elamanına
ise 0 özdeğerine uygun özelementi (özfonksiyonu) denir [17].
3.4. Metrik Uzaylar
X kümesi ve d : X  X 
dönüşümü için
 x , y  d  x , y 
1. d  x, y   0, d  x, y   0  x  y
2. d  x, y   d  y, x 
x, y  X
x, y  X
3. d  x, y   d  x, z   d  z, y 
x, y, z  X
özellikleri sağlanırsa X   X , d  uzayı metrik uzay olarak adlandırılır.
X   X , d  metrik uzayında bir  xn  dizisi ve bir x0 noktası verilsin. Eğer
d  xn , x0   0 ise,  xn  dizisi x0 noktasına yakınsıyor denir.
n 
 xn 
dizisi verilsin. Eğer d  xn , x0   0 olacak biçimde x0  X mevcutsa
n 
 xn  dizisine yakınsak dizi denir.
3.4.1. Tanım: X   X , d  metrik uzayı ve bu uzayda
 xn 
dizisi verilsin.
Eğer d  xn , xm   0 ise bu durumda  xn  dizisi Cauchy dizisi olarak adlandırılır.
n , m
3.4.2. Tanım: X   X , d  metrik uzayında her Cauchy dizisi yakınsak ise bu
uzaya Tam Metrik Uzay denir [28].
3.5. Normlu Uzaylar ve Banach Uzayları
E lineer uzayı
veya
cismi üzerinde ve  : E 
xE  x 
aşağıdaki şartların sağlandığını kabul edelim;
10
dönüşümü için
1. x  E için x  0 ve x  0  x  0
2. x  E ve  
x
 0  x  0
için  x    x
3. x, y  E için x  y  x  y
Bu durumda E lineer uzayında bir norm tanımlanmıştır denir.
x e x
elemanının normu, üzerinde norm tanımlanmış E lineer uzayına lineer normlu uzay
denir ve  E , 

şeklinde gösterilir. Lineer normlu uzayda d  x, y   x  y eşitliği
bir metrik tanımlar. Bu nedenle her normlu uzay aynı zamanda bir metrik uzay kabul
edilir. Eğer lineer normlu uzay tam ise (lineer normlu uzay d  x, y   x  y
metriğine göre metrik uzay olarak kabul edildiği için metrik uzaylardaki bütün
kavramlar lineer normlu uzaylar için de tanımlanmış olur) bu uzay Banach Uzayı
olarak adlandırılır [28].
3.6. İç Çarpım Uzayları ve Hilbert Uzayları
Kompleks sayılar cismi üzerinde E lineer uzayı verilsin. Bu uzayda her
x, y  E eleman çiftine
x, y
ile gösterilen bir tek kompleks sayı karşılık
getirilmişse ve de bu durumda her x, y, z  E ve her  kompleks sayısı için
1.
x, y  y, x
2.
 x, y   x, y
3.
x, x  0,
4.
x, y  z  x, y  x, z
x, x  0  x  0
şartları sağlanırsa, E ’de bir iç çarpım tanımlanmıştır.
elemanlarının iç çarpımı denir. E   E, , 
E   E, , 

x, y
sayısına x ve y
 ise iç çarpım uzayı olarak adlandırılır.
iç çarpım uzayında x 
x, x eşitliği ile bir norm tanımlar.
Bu nedenle her iç çarpım uzayı bir normlu uzay, dolayısıyla bir metrik uzay olarak
kabul edilir. Eğer E iç çarpım uzayı tam ve de sonsuz boyutlu ise (yani sonlu
boyutlu değilse) Hilbert uzayı olarak adlandırılır [28].
11
3.7. Hilbert Uzayında Simetrik Operatörler
H  Hilbert
Ax, y
H
 x, Ay
H
ve
uzayı
A : D  A  H  H
lineer
uzayı
verilsin.
eşitliği her x, y  D  A için sağlanıyorsa A operatörüne
simetrik operatör denir. Simetrik operatörlerin bütün özdeğerleri reel ve farklı
özdeğerlere uygun özfonksiyonları ortogonaldır [22].
3.8. L2  a,b  Uzayı ve Sobolev Uzayı
Verilmiş  a, b aralığında tanımlı ve Lebesgue anlamında ölçülebilir olan
f ( x)
fonksiyonu için
integrallenebilirse
f ( x)
2
fonksiyonu bu aralıkta Lebesgue anlamında
 a, b 
f ( x) fonksiyonuna
aralığında karesi integrallenebilir
fonksiyon denir. Karesi integrallenebilir fonksiyonların lineer uzayında
b
f , g :  f ( x) g ( x)dx
a
ile gösterilen bu formül bir iç çarpım tanımlar. Bu şekilde tanımlanan iç çarpım
uzayının bir Hilbert uzayı olduğu bilinmektedir. Bu uzay L2  a, b  ile gösterilir.
 a, b 
aralığı sonlu olduğu durumda L2  a, b  ’den olan her bir fonksiyonun  a, b 
aralığında Lebesgue anlamında integrallenebilir olacağı açıktır [17].
3.8.1. Tanım:  a, b  aralığında tanımlı ve lokal integrallenebilir olan u  x 
ve v  x  fonksiyonları verilsin. Eğer sonsuz mertebeden diferansiyellenebilir ve


Supp  x   x   0   a, b  şartını sağlayan her   x  fonksiyonu için
b
b
 u  x   x  dx   1  v  x   x  dx
 n
n
a
a
eşitliği sağlanıyorsa v  x  fonksiyonu u  x  fonksiyonunun n  n 

mertebeden
genelleştirilmiş türevi denir.
 a, b  
ile
 a, b 
aralığı q  1 reel sayısı ve m  0 tamsayısı verildiğinde Wqm  a, b 
aralığında Lebesque anlamında ölçülebilir ve u  x  , u  x  ,..., u 
12
m
 x
genelleştirilmiş türevleri bulunan ve her k  1, 2,..., m için u  k   x   L2  a, b  olan
fonksiyonların lineer uzayını göstereceğiz. Bu uzayda
u, v
W2m  a ,b 
 m
   u  k  , v k 
 k 0
1
2

L2  a ,b 

formülü bir iç çarpım tanımlıyor. Bu uzaylara Sobolev uzayları denir. Bu uzayların
Hilbert uzayları olduğu bilinmektedir. [26]
3.9. Kompleks Fonksiyonların Sıfır Yerlerinin Sayısı
3.9.1. Tanım: Bir f  z  kompleks fonksiyonu düzlemin keyfi bir z0
noktasının 
komşuluğunun tüm noktalarında diferansiyellenebiliyorsa
f  z
fonksiyonuna z0 noktasında analitiktir denir [16].
3.9.2. Tanım: Bütün kompleks düzlemde analitik olan fonksiyonlara tam
fonksiyon denir. Tam fonksiyonların sıfır yerlerinin sonlu veya en fazla sayılabilir
sayıda olduğu kompleks analizden bilinmektedir. f :
fonksiyonu ve z0 

ile tanımlı f  z 
noktası verildiğinde
f  z0   f   z0   ...  f  k 1  z0   0,
f  k   z0   0
ise bu durumda z  z0 noktasına f  z  fonksiyonunun k katlı sıfır yeri denir. Tam
fonksiyonların (sıfır olmayan) bütün sıfır yerlerinin sonlu katlı olduğu açıktır [25].
3.9.3. Rouche Teoremi: Eğer f  z  ve   z  kompleks fonksiyonları kapalı
düzlenebilir Jordan eğrisi olan  üzerinde ve içinde analitiklerse ve her z  için,
f  z    z
şartı sağlanıyorsa; o halde  eğrisinin içinde
f  z   z
fonksiyonun sıfır yerlerinin sayısı ile f  z  fonksiyonunun sıfır yerlerinin sayısı (her
sıfır yeri katı sayıda hesaplamak üzere) eşittir [24].
3.10. Mutlak ve Düzgün Yakınsaklık
ak   ak1 , ak 2 ,..., akn  
n
olmak üzere  ak  dizisi verilmiş olsun.
13


k 1
k 1
a1  a2  ...  ak  ...   ak    ak1 , ak 2 ,..., akn 
ifadesine
n
’de seri denir. Sk  a1  a2  ...  ak ’ya serinin kısmi toplamı ve  Sk 
dizisine ise serinin kısmı toplamlar dizisi denir ( k  1, 2,... )
 Sk  kısmi toplamlar dizisi a   a1, a2 ,..., an  

a
serisi a ’ya yakınsaktır denir ve

denir (Burada
a
k 1
k
k 1
k
n
’ye yakınsak ise

a
k 1
k
 a yazılır.  Sk  ıraksak ise seriye ıraksak
simgesinin yerine göre seriyi, yerine göre ise serisin toplamını
gösterdiğine dikkat ediniz) [1].
3.10.3. Tanım:
n
’de

 ak serisi verilmiş olsun. Eğer
k 1
yakınsak ise

a
k 1
k

a
k !
k
reel serisi
serisine mutlak yakınsak denir [1].
3.10.4. Tanım: f : S 

olmak üzere
 fk 
fonksiyon dizisi ve   0
sayısı verilmiş olsun. Bütün x ve k  k0  k0   için S ’de
fk  x   f  x   
olacak şekilde, sadece  ’a bağlı fakat x ’e bağlı olmayan bir k0 sayısı varsa
 fk  ,
S ’de düzgün yakınsaktır denir [1].
3.10.5. Teorem (Diziler için Cauchy Kriteri) : f k : S 
 fk 
dizisi ve   0 verilmiş olsun.

olmak üzere
 f k  ’nın düzgün yakınsak olması için gerek ve
yeter şart k  p  k0 için S ’de
fk  x   f p  x   
(3.10.1)
olacak şekilde bir k0  ’nin olmasıdır [1].
İspat:
 f  x 
k
dizisi S ’de f ’ye düzgün yakınsak ve   0 verilmiş olsun.
Bu takdirde her x  S ve her k  k0 için
fk  x   f  x  
14

2
vardır. Böylece her x  S ve k  p  k0 için
olacak şekilde k0 
f k  x   f p  x   f k  x   f  x   f ( x)  f p  x   f k  x   f  x   f p  x   f  x 

olur.
Tersine

2

olarak,

2

 0
verilmiş
sayısı
k  p  k0
ve
için
S ’de
f k  x   f p  x    olacak şekilde k0 pozitif tam sayısının olduğu yani (3.10.1)
Cauchy şartının sağlandığını farz edelim. Bu demektir ki her bir x  S için  f k  x  
dizisi bir Cauchy dizisi ve dolayısıyla yakınsaktır.
lim f k  x   f  x 
k 
olsun. Şimdi bu yakınsamanın düzgün olduğunu gösterelim. Eğer   0 verilmişse
fk  x   f p  x   
bu halle ilgili kabulden dolayı her x  S ve k  p  k0 için
olacak şekilde k0 
vardır. Bu takdirde her x  S için
lim f k  x   f p  x   f k  x   f  x    , k  k0
p 
yazabiliriz ve böylece f k  f dir.
3.10.6. Teorem (Weierstrass M-Kriteri): f k : A 

olmak üzere her
x  A için f k  x   M k olacak şekilde M k reel sayılar mevcut ve
yakınsak ise

f
k 1
k

M
k 1
k
serisi
serisi düzgün ve mutlak yakınsaktır [1].
İspat: Teoremi ispat etmek için (3.10.1) Cauchy şartının sağlandığını
göstermek yeterlidir. Hipotezden dolayı

M
k 1
k  p  k0 için
k
M
n  p 1
n
k
yakınsak olduğu için   0 ve
  olacak şekilde k0 sayısı vardır. Böylece genelleştirilmiş
üçgen eşitsizliğinden
Sk  x   S p  x  
k

n  p 1
fn  x  
15
k

n  p 1
fn  x  
k
M
n  p 1
n

yazılabilir. Demek ki her x  A için Sk  x   S p  x    ve böylece
A da düzgün yakınsaktır. Ayrıca son eşitsizlikten dolayı

 f  x
k 1
k
serisi

 f  x
serisi de
k 1
yakınsaktır.
3.11. SDP’nin Çözümünün Varlığı, Tekliği ve Parametreye Göre Tamlık
Teoremi
q :  a, b 
ile tanımlı q  x  fonksiyonun sürekli bir fonksiyon olduğunu
kabul edelim. O halde
u  q  x  u  u,
x   a, b
diferansiyel denkleminin
u  a   sin  ,
u  a    cos  ,
  0,  
sınır şartlarını sağlayan bir tek u  x,   çözümü bulunur ve bu çözüm her x   a, b
için  
parametresinin tam fonksiyonudur [25].
3.12. Asimptotik Davranışlar
Verilmiş f  x  fonksiyonunun x   için davranışı bazı durumlarda bilinen
“basit”
g  x  fonksiyonunun x   için davranışından yararlanılarak ifade
edilebilir. Böyle durumlarda f  x  ve g  x  in x   için davranış “yakınlığı”
incelenirken “ o ”, “ O ”, “ ” gibi simgelerden yararlanılmaktadır. Ayrıca, x  
için g  x  üzerine önceden hiçbir şart konulmamaktadır.
Kompleks düzlemin herhangi G 
h  z  fonksiyonları verilsin. Eğer
f  z
g  z
bölgesinde tanımlı olan f  z  , g  z  ve
fonksiyonu bu bölgede sınırlı ise, yani;
z  G  z : z  R
f  z  M g z ,
eşitsizliği sağlanacak şekilde R  0, M  0 sayıları mevcutsa
f  z   O  g  z  ,
16
z  G,
z 
(3.12.1)
şeklinde yazılır. Bu ifadeye asimptotik eşitlik denir. Eğer,
f  z   h  z   O  g  z  ,
z  G,
z 
f  z   h  z   O  g  z  ,
z  G,
z 
ise
(3.12.2)
yazılır. z0  G verilsin. Bu taktirde
f  z
lim
g  z
z  z0 , zG
f  z   o  g  z  ,
0
z  G,
z 
(3.12.3)
yazılır ve f  z  fonksiyonu z  0  noktasının yakın komşuluğunda g  z  ye göre
sonsuz küçüktür denir.
f  z
g  z
fonksiyonu z  0  noktasının herhangi komşuluğunda
sınırlı ise
f  z   O  g  z  ,
z  G,
z  z0
(3.12.4)
z  z0
(3.12.5)
yazılır. Eğer
lim
z  z0
f  z
g  z
1
ise
f  z
g  z,
z  G,
yazılır. Hangi G bölgesinden bahsedildiği açık şekilde bilinirse z  G yazısı atılır.
an  , bn 
a 
ve cn  reel veya kompleks sayı dizileri verildiğinde  n  dizisi sınırlı
 bn 
olduğunda
an  O  bn 
(3.12.6)
yazılır. an  cn  O  bn  olduğunda ise bu eşitlik
an  cn  O  bn 
şeklinde gösterilir.
an
0
n  b
n
lim
olduğunda bu eşitlik
17
(3.12.7)
an  o  bn 
(3.12.8)
şeklinde gösterilir. an  cn  o  bn  olduğunda ise bu eşitlik
an  cn  o  bn 
(3.12.9)
şeklinde gösterilir. (3.12.1)-(3.12.9) şeklindeki formüllere asimptotik formüller denir
[25].
3.13. Sturm-Liouville Problemleri
H  herhangi Hilbert uzayı L : H  H ise bu uzayda tanımlı olan lineer
operatör olsun. Eğer herhangi 0 skaleri için ( H uzayının cisminden alınmış)
Ly0  0 y0 olacak biçimde y0  H , y0  0 elemanı bulunursa, 0 sayısına L
operatörünün özdeğeri, y0 elemanına ise bu özdeğere uygun olan özeleman (veya
özvektör) denir. Uygulamalarda sık sık rastlanan diferansiyel operatörlerden biri de
L
d
 q( x)
dx 2
biçiminde ifade edilen operatördür (bu operatör genelde H  L2  a, b  biçimindeki
Hilbert uzaylarında incelenmektedir). L  operatörü için en önemli sınır şartları
y (a) cos   y(a)sin   0

y (b) cos   y(b)sin   0 
(3.13.1)
 ,   0,    biçiminde veya
y  a   y  b  

y  a   y  b  
(3.13.2)
biçiminde verilmiş sınır şartlarıdır.
Ly  x    y  q  x  y   y
denkleminin (3.13.1) veya (3.13.2) tipindeki sınır şartlarını sağlayan çözümlerinin
bulunması problemi klasik Sturm-Liouville problemi olarak adlandırılır.
Eğer  a, b aralığı sınırlı, g  x  fonksiyonu ise integrallenebilir ise o halde
böyle problemlere Regüler Sturm-Liouville problemleri denir. Daha genel olan
y  p  x  y    x   r  x  y  0
18
(3.13.3)
biçimindeki diferansiyel denklemlerde  x, y  değişkenlerinden  t , u  değişkenlerine
x
t
 r  s ds
a
b
x
u  t   4 r  x e
,
 r  s ds
1
p  s  ds
2

a
y  x
a
Laplace dönüşümü ile geçersek, (3.13.3) denklemi
u  q  t  u  u
denklemine dönüşür. Burada r  x   0 olmak üzere, ikinci mertebeden sürekli
diferansiyellenebilir
bir
p  x
fonksiyon;
ise
1.
diferansiyellenebilir fonksiyondur. Ayrıca bu durumda
mertebeden
 a, b 
sürekli
aralığı da
0,1
aralığına dönüşmüş olur [14].
3.13.1. Wronskian Determinantı
f , g  C1 herhangi iki fonksiyon olmak üzere
Wx  f , g  
f  x g  x
 f  x g  x  f   x  g  x 
f   x g  x
şeklinde tanımlanan determinanta Wronskian determinantı denir [13].
3.13.2. Teorem: a0 , a1 ,..., an fonksiyonları bir I açık aralığında sürekli ve bu
aralıktaki x için a0  x   0 olsun. Bu takdirde
Ly  a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  0
(3.13.4)
homojen lineer diferansiyel denkleminin y1 , y2 ,..., yn çözümlerinin I da lineer
bağımsız olması için gerek ve yeter koşul, I aralığındaki her x için
W  y1 , y2 ,..., yn  x   0
olmasıdır [6].
İspat: Önce koşulun, yeter bir koşul olduğunu ispat edelim. Bunun için
(3.13.1) homojen lineer denkleminin y1 , y2 ,..., yn çözümlerinin Wronkskianının
I aralığındaki her x için sıfırdan farklı, fakat bu çözümlerin I da lineer bağımlı
19
olduğunu varsayalım. Bu takdirde hepsi birden sıfır olmayan b1 , b2 ,..., bn sabitleri ve
I aralığındaki her x için
b1 y1  x   b2 y2  x   ...  bn yn  x   0
(3.13.5)
b1 y1  x   b2 y2  x   ...  bn yn  x   0
(3.13.6)
b1 y1
n 1
 x   b2 y2 n1  x   ...  bn yn n1  x   0
bağıntıları sağlanır. I aralığındaki her x için (3.13.5) ve (3.13.6) bağıntılarına,
b1 , b2 ,..., bn bilinmeyenlerine göre bir homojen cebirsel denklem sistemi olarak
bakılabilir. Bu sistemin katsayılar determinantı, açıkça W  y1 , y2 ,..., yn  x  dir.
y1 , y2 ,..., yn çözümleri I da lineer bağımlı varsayıldığından, söz konusu homojen
cebirsel denklem sistemi aşikar olmayan bir çözüm takımına sahip olmalıdır. Bunun
için, homojen cebirsel denklem sistemleri teorisinden bilindiği üzere, I aralığındaki
her x için sistemin katsayılar determinantı sıfır, yani
W  y1 , y2 ,..., yn  x   0
olmalıdır. Bu I aralığındaki her için W  y1 , y2 ,..., yn  x   0 kabulüyle çelişir.
Demek ki, her x  I için W  y1 , y2 ,..., yn  x   0 ise, (3.13.4) homojen lineer
diferansiyel denkleminin y1 , y2 ,..., yn çözümleri I da lineer bağımsızdır.
Şimdi koşulun, gerek bir koşul olduğunu ispat edelim. Bunun için,
a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  0
homojen lineer denkleminin y1 , y2 ,..., yn çözümlerinin I da lineer bağımsız, fakat I
nın hiç olmazsa bir x0 noktasında W  y1 , y2 ,..., yn  x0   0 olduğunu varsayalım.
x  x0 için (3.13.5) ve (3.13.6) cebirsel denklem sistemini tekrar göz önüne alalım.
b1 y1  x0   b2 y2  x0   ...  bn yn  x0   0
(3.13.7)
 n 1
b1 y1
 x0   b2 y2
 n 1
 x0   ...  bn yn
 n 1
 x0   0
sistemi, W  y1 , y2 ,..., yn  x   0 olduğundan, en az bir b1 , b2 ,..., bn çözüm takımına
sahiptir ve bi lerin hepsi birden sıfır değildir.
Şimdi (3.13.5) nin bir çözümü olan bu b1 , b2 ,..., bn sabitleriyle
20
  x   b1 y1  x   b2 y2  x   ...  bn yn  x 
fonksiyonunu tanımlayalım. Bu fonksiyon
a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  0
homojen denkleminin bir çözümüdür ve (3.13.7) gereğince
  x0   0,    x0   0, ... ,   n1  x0   0
Başlangıç koşullarını sağlar. Böylece I aralığındaki her x için   x   0 dır.
Buradan, I aralığındaki her x ve hepsi birden sıfır olmayan b1 , b2 ,..., bn sabitleri için
b1 y1  x   b2 y2  x   ...  bn yn  x   0
elde edilir. Bu y1 , y2 ,..., yn lerin I da lineer bağımsız olduğu varsayımıyla çelişir.
Demek ki
a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  0
homojen lineer diferansiyel denkleminin y1 , y2 ,..., yn çözümleri I da lineer bağımsız
ise, I daki tüm x ler için W  y1 , y2 ,..., yn  x   0 dır.
3.14. İkinci
Mertebeden
Lineer
Diferansiyel
Denklemler
İçin
Paramatrelerin Değişimi Yöntemi:
Parametrelerin değişimi yöntemi
a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  Q  x 
(3.14.1)
denklemine ait
a0  x  y n  a1  x  y n1  ...  an1  x  y  an  x  y  0
homojen lineer denkleminin n lineer bağımsız çözümünün (dolayısıyla genel
çözümünün) bilinmesi halinde (3.14.1) denkleminin bir özel çözümünün
bulunmasında etkilidir. Yöntemi önce, ikinci mertebeden
a0  x  y  a1  x  y  a2  x  y  Q  x 
(3.14.2)
denklemi için açıklayalım. (3.14.2) ‘ye ait
a0  x  y  a1  x  y  a2  x  y  0
homojen lineer denkleminin
21
(3.14.3)
yh  C1 y1  x   C2 y2  x 
(3.14.4)
genel çözümünün bilindiğini varsayalım. Burada C1 ve C2 keyfi sabitlerdir. (3.15.4)
de C1 ve C2 yerine sırasıyla v1  x  , v2  x  fonksiyonlarını alarak
y p  v1  x  y1  x   v2  x  y2  x 
(3.14.5)
fonksiyonunu teşkil edelim. Acaba v1  x  ve v2  x  , (3.14.5) ifadesi (3.14.2)
denkleminin bir çözümü olacak şekilde belirtilebilinir mi? Soruyu cevaplandırmak
için (3.14.5) deki y p yi ve bunun
y p  v1 y1  v2 y2  v1 y1  v2 y2
y p  v1 y1  2v1 y1  v2 y2  2v2 y2  v1 y1  v2 y2
türevlerini (3.14.2) denkleminde yerlerine koyalım. Gerekli düzenlemelerden sonra
 


 a v  y  v  y   a v  y   v  y    a v  y  v  y 

Q  x   a0 y1  a1 y1  a2 y1 v1  a0 y2  a1 y2  a2 y2 v2
0
1
1
2
2
0
1
1
2
2
1
1
1
2
(3.14.6)
2
elde edilir. y1 ve y2 (3.14.3) homojen lineer denkleminin çözümleri olduğundan v1
ve v2 nin katsayıları sıfırdır. Böylece (3.14.6)


 



a0 v1 y1  v2 y2  a0 v1 y1  v2 y2  a1 v1 y1  v2 y2  Q  x 
(3.14.7)
olur.
v1 ve v2 fonksiyonlarını belirtmek için, bunlar arasında iki bağıntı bulmak
yeterlidir. I aralığındaki her x için v1 y1  v2 y2  0 seçilirse, (3.14.7) ifadesinden I


aralığındaki her x için a0 v1 y1  v2 y2  Q  x  bulunur. Yani v1 ve v2 için
v1  x  y1  x   v2  x  y2  x   0
v1  x  y1  x   v2  x  y2  x  
Q  x
a0  x 
(3.14.8)
denklemleri elde edilir. (3.14.8), her x  I için v1 , v2 bilinmeyenlerine göre
homojen olmayan bir lineer cebirsel denklem sistemi olarak düşünülebilir. Bu
sistemin katsayılar determinantı
22
y1  x 
y2  x 
y1  x 
y2  x 
dir. Bu, (3.14.3) homojen lineer diferensiyel denkleminin lineer bağımsız y1 , y2
çözümlerinin Wronskianıdır ve Teorem 3.13.2 gereğince sıfırdan farklıdır.
Dolayısıyla (3.14.8) sistemi bir ve yalnız bir
v  x  , v  x 
1
2
çözüm takımına
sahiptir. v1 ve v2 x ’in fonksiyonları olup bunların integralleri v1  x  ve v2  x 
fonksiyonlarını verir. Demek ki, v1  x  , v2  x  fonksiyonları (3.14.5) fonksiyonu
(3.14.2) denkleminin bir çözümü olacak şekilde belirtilebilir.


Şimdi varsayalım ki, v1  x  , v2  x  (3.14.8) sisteminin (tek) çözümüdür.
Bu
takdirde,
aşikar
olarak,
x  I için
her
(3.14.7)
sağlanır.
Yani
y p  v1  x  y1  x   v2  x  y2  x  fonksiyonu (3.14.2) denkleminin bir çözümüdür [6].
Sonucu bir teorem olarak ifade edelim.
Teorem 3.14.1. a0 , a1 , a2 ve Q fonksiyonları bir I açık aralığında sürekli ve
I da a0  x   0 olsun. y1 ve y2 I da (3.14.3) homojen lineer diferensiyel
denkleminin lineer bağımsız iki çözümü olsun. Eğer v1 ve v2 fonksiyonları
v1  x  y1  x   v2  x  y2  x   0
v1  x  y1  x   v2  x  y2  x  
Q  x
a0  x 
sistemini sağlıyorsa, y p  v1  x  y1  x   v2  x  y2  x  fonksiyonu (3.14.2) denkleminin
bir çözümüdür [6].
3.15. Green Fonksiyonu
Aşağıdaki
şartları
sağlayan
G  x,   :  a, b   a, b  C
fonksiyonuna
L operatörünün Green Fonksiyonu denir.
1. G  x,   fonksiyonu süreklidir ve x ’e göre  n  2  . mertebeye kadar (bu
mertebe dahil) bütün sürekli türevleri vardır.
23
2. Her    a, b  için
fonksiyonunun
 n  2 .
 a,  
ve
 ,b
aralıklarının her birinde G  x,  
ve n . mertebeden türevleri var ve x ’e göre
 n  1 .
mertebeden türev fonksiyonu
 n1
 n1
1
G   0,    n1 G   0,   
n 1
x
x
p0  
özelliğine sahiptir.
3. Her bir  a,   ve  ,b aralığında G  x,   fonksiyonu x değişkeninin
fonksiyonu gibi
G   0 ,
U v  G   0, v  1, n sınır değer probleminin çözümüdür
[17].
24
4. MATERYAL ve METOD
Bu tez çalışmasında materyal olarak kaynaklar kısmında verilen kitap ve
makalelerden ve gerekirse çalıştığımız konu ile ilgili yeni kaynaklardan
yararlanılmıştır. Bu kaynaklarda uygulanan yöntemler incelenerek tez konumuzdaki
probleme uygulanabilir hale dönüştürülmüştür. Adi diferansiyel denklemler için sınır
değer problemlerinin özdeğerlerinin asimptotik davranışlarının incelenmesi için
uygulanan karakteristik fonksiyonun kurulması yönteminden, klasik Sturm-Liouville
teorisi yöntemlerinden, fonksiyonel analizden bazı temel tanımlar ve simetrik
operatörlerin bazı temel özelliklerden, kompleks analizdeki tam fonksiyonların sıfır
yerleri ile ilgili olan teoremlerden, son yıllardaki çalışmalarda uygulanan
yöntemlerden ve asimptotik yöntemlerden yararlanılmıştır.
25
5. BULGULAR VE TARTIŞMA
5.1. Sınır Değer Probleminin İfadesi
Bu bölümde
 u : u  q  x  u  u
(5.1.1)
Sturm-Liouville denkleminden,
 1u  0   2u  0     1u  0   2u  0 
(5.1.2)
  3u( )  4u( )    3u( )   4u( ) 
(5.1.3)
sınır şartlarından oluşan sınır değer probleminin özdeğer ve özfonksiyonları
0,  
incelenmiştir. Burada q  x  ,
aralığında sürekli ve  kompleks özdeğer
parametresidir.
5.2. Verilen Sınır Değer Problemi İle Aynı Özdeğere Sahip Olan Lineer
Operatörün Kurulması
Üç
bileşenli
 f ( x) 


F   F1  ,
 F 
 2 
f  x   L2  0,   ,
elemanların lineer uzayını H  L2 0,    
1 
1
2
1
,
2
F1 , F2 
biçimindeki
ile gösterelim. Eğer
2 
3
4
3
4
olmak üzere 1  0 , 2  0 kabul edersek
 f  x 


F   F1   H ,
 F 
 2 
 g  x


G   G1   H
 G 
 2 
için

F , G   f  x  g  x dx 
0
1
1
F1 G1 
1
2
F2 G2
(5.2.1)
iç çarpımına göre H lineer uzayı bir Hilbert uzayı tanımlar. Bu Hilbert uzayı (5.1.1)(5.1.3) sınır değer problemine uygun Hilbert uzayıdır. İşlemlerin kolaylığı için
26
N1  u   1u  0    2u  0  ,
N1  u   1u  0    2u  0 
N 2  u   3u     4u   ,
N 2  u   3u     4u  
ifadelerini tanımlayalım. Diğer taraftan f  x  ve g  x  fonksiyonlarının Wronskian
determinantını
W  f , g; x   f  x  g   x   f   x  g  x 
şeklinde gösterirsek,
N1  f  N1  g   N1  f  N1  g   1W  f , g ;0 
(5.2.2)
N 2  f  N 2  g   N 2  f  N 2  g   2W  f , g ;  
ifadelerini elde ederiz. Gerçekten;


f  0   g 0   g 0
N1  f  N1  g   N1  f  N1  g    1 f  0    2 f   0   1 g  0    2 g   0 

 1 f  0    2
1
2
 11 f  0  g  0   1 2 f  0  g   0 
 1 2 f   0  g  0    2  2 f   0  g   0 
 11 f  0  g  0   1 2 f  0  g   0 
 1 2 f   0  g  0    2  2 f   0  g   0 

 1 2  1 2
  f 0  g  0   f  0  g 0 
 1W  f , g ;0 
olduğu görülür. Benzer şekilde

N 2  f  N 2  g   N 2  f  N 2  g     3 f      4 f      3 g     4 g   



  3 f     4 f      3 g     4 g    
  3  3 f   g     3  4 f   g   
  3  4 f    g     4  4 f    g   
  3  3 f   g     3  4 f   g   
  3  4 f    g     4  4 f    g   

 3  4  3  4
  f   g     f    g   
  2W  f , g ;  
eşitliği gösterilebilir. Buna göre (5.1.1)-(5.1.3) sınır değer problemine uygun
A : H  H operatörünü
27
 f  x  




D  A   N1  f    H f  x  W22  0,   
 N  f  


 2

  f   q  x 

A  F    N1  f 
 N  f 
2

f




(5.2.3)
(5.2.4)
 f  x 


eşitlikleri ile tanımlayım. Burada F  D  A ve F   N1  f   dır. Yani A operatörü
 N  f 
 2

 f  x     f   q  x 

 
A  N1  f     N1  f 
 N  f    N  f 
2
 2
 
f




biçiminde tanımlıdır. O halde,
AF   F
(5.2.5)
eşitliği,
  f   q  x 

N1  f 

 N  f 
2

 f  x 
f



    N1  f  

 N  f 

 2

(5.2.6)
biçiminde yazılır. (5.2.6) eşitliğinden
 f   q  x  f   f
 1 f  0    2 f   0     1 f  0    2 f   0 
N1  f    N1  f 
  3 f     4 f      3 f     4 f    
 N2  f    N2  f 
 f  x 


elde edilir. Ayrıca F   F1   D  A  olduğu için F1  N1  f  ve F2  N 2  f 
 F 
 2 
eşitlikleri sağlanır. O halde, (5.1.1)-(5.1.3) sınır değer problemi
28
 u  x 


U   N1  u  
 N u  
 2

olmak üzere AU  U biçiminde yazılabilir. Tanımladığımız bu A operatörün
simetrik olduğu (5.2.2) ifadeleri gereği açıktır.
5.2.1.Teorem: H  L2  0,    
Hilbert
uzayında
(5.2.3)-(5.2.4)
eşitlikleriyle tanımlı A operatörü simetriktir.
İspat: Her F , G  D  A için
AF , G  F , AG
olduğunu göstermemiz
gerekir. Gerçekten H Hilbert Uzayındaki iç çarpımın tanımı gereği

A  F  , G     f   x   q  x  f  x  g  x  dx 
0


0
0
1
1
N1  f  N 1  g  
   f   x g  x  dx   q  x  f  x g  x  dx 

1
2
1
1
1
2
N2  f  N2  g 
N1  f  N1  g 
N2  f  N2  g 
yazabiliriz. Son eşitliğin birinci integraline

 f   x  dx  dv , f   x   v


 g  x   u , g   x  dx  du
şeklinde kısmi integrasyon uygulanırsa;



  f   x  g  x d  x    g  x  f   x  |   f   x  g   x dx
0
0
(5.2.7)
0
olur. Bulunan bu eşitliğin sağ tarafındaki integrale

 f   x  dx  dt , f  x   t


 g   x   z , g   x  dx  dz
şeklinde kısmi integrasyon uygulanırsa;




f   x  g   x d  x   g   x  f  x  |   f  x  g   x dx
0
0
0
elde edilir. (5.2.7) ve (5.2.8) eşitliklerinden yararlanılarak AF , G ifadesi
29
(5.2.8)


0
0

AF , G    f  x  g   x dx   q  x  f  x  g  x dx  g  x  f   x  |

1
0
1
 g  x f  x | 
0
N1  f  N1  g  


0
0
1
N2  f  N2  g 
2
   f  x  g   x dx   q  x  f  x  g  x dx  g   f     g  0  f   0 
 g    f    g   0  f  0  


0
0
1
1
N1  f  N1  g  
1
2
N2  f  N2  g 
   f  x  g   x dx   q  x  f  x  g  x dx  W  f , g ;    W  f , g ;0 

1
1
N1  f  N1  g  
1
2
N2  f  N2  g 
şeklinde yazılır. Diğer taraftan H uzayındaki iç çarpımın tanımı gereği

F , AG   f  x    g   x   q  x  g  x  dx 
0


0
0
1
1
N1  f  N1  g  
   f  x  g   x dx   f  x q  x  g  x dx 
1
1
1
2
N2  f  N2  g 
N1  f  N1  g  
1
2
N2  f  N2  g 
dir. Üstteki iki eşitlik taraf taraf çıkarılırsa ve (5.2.2) ifadelerinden yararlanılırsa;
AF , G  F , AG  W  f , g ;    W  f , g ;0  

1
1
N1  f  N1  g  
1
2
1
1
N1  f  N1  g  
1
2
N2  f  N2  g 
N2  f  N2  g 
 W  f , g ;    W  f , g ;0   W  f , g ;0   W  f , g ;  
0
elde edilir. Dolayısıyla her F , G  D  A için, AF , G  F , AG eşitliği bulunur.
5.2.2. Sonuç: Eğer 1  12  12  0 ve 2  3 4  3 4  0 şartları
sağlanıyorsa (5.1.1)-(5.1.3) sınır değer probleminin bütün özdeğerleri reeldir.
İspat:  sayısının (5.1.1)-(5.1.3) sınır değer probleminin özdeğeri olduğunu
kabul edelim. Bu durumda  sayısı (5.2.3)-(5.2.5) eşitlikleri ile tanımlı A
operatörünün özdeğeri olacaktır. Dolayısıyla U 0 , A operatörünün  özdeğerine
uygun herhangi bir öz elementi olmak üzere
 U 0 ,U 0
H
 U 0 ,U 0
H
 AU 0 ,U 0
H
 U 0 , AU0
eşitliğini elde ederiz. Buradan
30
H
 U0 , U0
H
  U 0 ,U 0
H
(   ) U 0 ,U 0
yazabiliriz. U 0 ,U 0
0
H
 0 olduğundan     0 dolayısıyla    bulunur. Bunun
H
anlamı bütün özdeğerler reeldir.
5.2.3. Sonuç: Eğer 1  12  12  0 ve 2  3 4  3 4  0 şartları
sağlanıyorsa (5.1.1)-(5.1.3) sınır değer probleminin iki farklı  ve  özdeğerlerine
karşılık gelen u  x  ve u  x  özfonksiyonları için aşağıdaki eşitlik sağlanır.

1
 u  x u  x  dx   
N1  u  x   N1  u  x   
1
0
1
2
N 2  u  x   N 2 u  x  
(5.2.9)
İspat: H - Hilbert uzayında (5.2.4) ile tanımlı A operatörü için
 u ( x) 


U  :  N1 (u ( x)) 
 N 2 (u ( x)) 


 u ( x) 
U  :  N1 (u ( x))  ,
 N 2 (u ( x)) 
elemanlarının  ve  özdeğerlerine karşılık gelen öz elementleri olduğu açıktır. 
ve  özdeğerlerinin reel ve A operatörünün H -Hilbert uzayında simetrik olduğunu
dikkate alırsak,
 U  ,U 
H
 U  ,U 
H
 AU  ,U 
H
H
  U  ,U 
H
 U  , AU 
H
 U  , U 
H
  U  ,U 
H
bulmuş oluruz. Buradan
 U  ,U 
(   ) U  ,U 

H
0
yazılabilir.    olduğundan
U  ,U 
H
0
(5.2.10)
dır. O halde H-Hilbert Uzayında tanımlamış olduğumuz (5.2.1) iç çarpım formülünü
dikkate alırsak (5.2.9) ile (5.2.10) ifadelerinin eşdeğer olduğu görülür.
5.3. Sınır Değer Problemi İle İlgili Bazı Yardımcı Başlangıç- Değer
Problemlerinin
Çözümleri
ve
Bu
Çözümlerin
Özdeğer
Parametresine Göre Analitikliği
Bu bölümde verilen
u  q  x  u  u,
denkleminin
31
x  0,  
(5.3.1)
 1u  0   2u  0     1u  0   2u  0 
(5.3.2)
  3u    4u      3u    4u  
(5.3.3)
sınır şartlarını sağlayan çözümünü araştırmak için bazı yardımcı başlangıç-değer
problemlerinin çözümlerinin mevcutluğu ve bu çözümlerin  kompleks özdeğer
parametresine göre bütün kompleks düzlemde analitikliği gösterilecektir. Daha sonra
(5.3.1) denkleminin (5.3.1)-(5.3.3) problemi
için temel
olacak çözümleri
tanımlanacaktır.
5.3.1. Teorem: Her  
için
u  q  x  u  u,
x  0,  
(5.3.4)
u  0   2  2
(5.3.5)
u  0   1  1
(5.3.6)
başlangıç değer probleminin, bir tek u    x  çözümü mevcuttur ve ayrıca
x  0,   değişkeninin her bir değerinde   x  fonksiyonu  parametresinin tam
fonksiyonundur.
İspat: Adi diferansiyel denklem teorisinden çok iyi bilinen ve bu teorinin en
temel teoremlerinden biri olan Cauchy-Picard teoremi gereği (5.3.4)-(5.3.6)
başlangıç-değer probleminin (Cauchy probleminin) her  
için bir tek   x 
çözümü mevcuttur. Bu teoremin esas ve önemli olan kısmını, yani   x 
çözümünün, değişkenin her bir x  0,   değeri için  
değişkenine göre bütün
kompleks düzlemde analitik olduğunu ispat edelim.   x  fonksiyonu her x  0,  
ve her  
için (5.3.4) denklemini sağladığından
  x     q  x    x 
denklemini sağlayacaktır. Burada her iki tarafının  0, x  aralığında integrali alınırsa,
x
  x       q  t    t  dt  C1   
(5.3.7)
0
biçiminde eşitlik elde edilir.  ’ya bağlı olan C1    ifadesini bulmak için (5.3.7) de
x  0 yazarsak
32
  x   C1   
(5.3.8)
eşitliği elde edilir. Diğer taraftan  fonksiyonunun tanımı gereği,
  0   1  1
(5.3.9)
eşitliği sağlanır. (5.3.8) ve (5.3.9) ifadelerinden
C1     1  1
(5.3.10)
eşitliği elde edilir. (5.3.10) ifadesi (5.3.7) de yerine yazılırsa her x  0,   ve her

için geçerli olan
x
  x       q  t    t  dt 1  1
(5.3.11)
0
eşitliği elde edilir. (5.3.11) eşitliği  0, x  aralığında integrallenirse,
x
s
0
0
  x    ds     q  t    t  dt  x  1  1   C2   
(5.3.12)
eşitliği elde edilir. Bu eşitliği x  0 için yazarsak   x  fonksiyonunun (5.3.5)
başlangıç şartını sağladığını da dikkate alırsak,
C2       0 
(5.3.13)
eşitliği elde edilir. Diğer taraftan  fonksiyonunun tanımı gereği,
  0   2  2
(5.3.14)
eşitliği sağlanır. (5.3.13) ve (5.3.14) ifadelerinden
C2     2  2
(5.3.15)
eşitliği elde edilir. (5.3.15) ifadesi (5.3.12) de yerine yazılırsa,
x
s
0
0
  x    ds     q  t    t  dt  x  1  1    2   2
(5.3.16)
olur. Eşitliğin sağ tarafındaki integral ifadede integralleme sırası değiştirilirse,
x
x




0 ds 0   q t   t  dt  0 dt t   q t   t  ds   0   q t   t  x  t  dt
eşitliği bulunur. Son eşitliği (5.3.16) de yerine yazarsak her x  0,   ve her  
x
s
x
için geçerli olan
33
x
  x       q  t    t  x  t  dt  x  1  1    2   2
(5.3.17)
0
eşitliği (özdeşliği) elde edilir. Böylece   x  çözüm fonksiyonu için (5.3.17)
biçiminde verilmiş integral denklem elde edildi. Bu integral denklemin çözümüne
(yani   x  fonksiyonuna) yakınsayan fonksiyon dizisinin inşa edilmesi için,
integral denklemler teorisinden iyi bilinen ardışık yaklaşma yönteminden
yararlanılacaktır. Bu yöntem gereği aşağıdaki rekurrent (ard-arda birbirini üreten)
fonksiyonlar dizisi inşa edilecektir.


 x   x  1  1   2  2
0
(5.3.18)
x
n
 x      x      q  t    t  x  t  dt ,
n1
0
n  1, 2,...
(5.3.19)
0
M : max q  t 
K     max 0   t  gösterimlerinden yararlanılarak
ve
t0, 
t0, 


R  0 keyfi sayı olmak üzere  n   x  fonksiyonlar dizisinin herhangi kapalı ve
sınırlı   R yuvarında


0
  x       x      x 
n 1
n
(5.3.20)
n1
fonksiyonlar dizisinin yakınsaklık durumu incelenecektir. Bu fonksiyonlar dizisi ile
  x  fonksiyonlar dizisinin ya her ikisinin yakınsak ya da her ikisinin ıraksak
n
oldukları ve de yakınsak oldukları durumda verilmiş (5.3.20) serisinin toplamı ile
  x  dizisinin limitinin aynı olduğu açıktır. Bu nedenle   x  dizisi yerine
n
n
(5.3.20) serisi incelenecektir. Bu serinin terimleri ard arda değerlendirilecektir.
   x 
1
x
0
x
  x   
  q  t     t  x  t  dt    R  M  K    x  t  dt
0
0
0

1
 R  M  K    x2
2
eşitsizliği bulunur.

x
n
 x      x      q  t     t  x  t  dt
n1
0
0
34
(5.3.21)

x
n1
  x     x   
   q  t  
0
n 2 
t  x  t  dt
0
ifadelerinden yararlanılarak n  2 için geçerli olan

x
n
  x    x   
   q  t     t   
n1
n1
n2 
t   x  t  dt
(5.3.22)
0
eşitliği elde edilir. (5.3.21) eşitsizliğinden ve (5.3.22) eşitliğinden yararlanılarak
(5.3.20) serisinin diğer terimleri değerlendirilecektir. n  2 için

x
2
 x      x      q t    t     t   x  t  dt
1
1
0
0
x

1
2
 R  M  K     t 2  x  t  dt
2
0
  R  M  K  
2
x4
4!
bulunur. Böyle devam ederek tümevarım yöntemi ile

 x   n1   x    R  M  K   
n
n
x2n
, n=1,2,...
 2n  !
(5.3.23)
eşitsizliğinin her n  1 için sağlandığı kolayca bulunur. x  0,   olduğu için
0  x2n   2n olur. Dolayısıyla (5.3.23) ifadesinden
 R  M   2  K   
 n   x    n1   x  
 2n  !
n
eşitsizliği elde edilir.
n
( R  M ) 2  K ( )
K    
(2n)!
n 1

sayısal serisi yakınsak olduğundan Weierstrass M-Kriteri gereği (5.3.20) serisi
mutlak ve düzgün yakınsaktır.
  x  fonksiyonlarının
n
(5.3.18) ve (5.3.19)
eşitlikleri ile verilmiş tanımları gereği bu fonksiyonların her biri her x  0,   için
 
:   R bölgesinde analitik olduğundan ve her x  0,   için
  x 
n
dizisi   x  fonksiyonuna düzgün olarak yakınsak olduğundan  ( x) fonksiyonu da
her x  0,   için  değişkeninin tam fonksiyonudur.
35
5.3.2. Sonuç:   x  fonksiyonu (5.3.1) denklemini ve (5.3.2) sınır şartını
sağlayan ve her x  0,   için  parametresinin tam fonksiyonu olan çözümdür.
5.3.3. Teorem: Her  
için
u  q  x  u  u,
x  0,  
(5.3.24)
u    4  4
(5.3.25)
u    3  3
(5.3.26)
başlangıç değer probleminin, bir tek u    x  çözümü mevcuttur ve ayrıca
x  0,   değişkeninin her bir değerinde    x  fonksiyonu  parametresinin tam
fonksiyonudur.
İspat: Adi diferansiyel denklem teorisinden çok iyi bilinen ve bu teorinin en
temel teoremlerinden biri olan Cauchy-Pikard teoremi gereği verilmiş (5.3.24)(5.3.26) başlangıç-değer probleminin (Cauchy probleminin) her  
için bir tek
 ( x) çözümü mevcuttur. Bu teoremin esas ve önemli olan kısmını, yani  ( x)
çözümünün, değişkeninin her bir x  0,   değeri için  
değişkenine göre bütün
kompleks düzlemde analitik olduğunu ispat edelim.    x  fonksiyonu her x  0,  
ve her  
için (5.3.24) denklemini sağladığından
  x     q  x    x 
denklemini sağlayacaktır. Burada her iki tarafının  x,   aralığında integrali alınırsa,

   x       q  t     t  dt C1   
(5.3.27)
x
biçiminde eşitlik elde edilir.  ’ya bağlı olan C1    ifadesini bulmak için (5.3.27)
ifadesinde x   yazarsak
     C1   
(5.3.28)
eşitliği elde edilir. Diğer taraftan   fonksiyonunun tanımı gereği,
    3  3
(5.3.29)
eşitliği sağlanır. (5.3.28) ve (5.3.29) ifadelerinden
C1     3  3
36
(5.3.30)
Eşitliği elde edilir. (5.3.30) ifadesi (5.3.27) de yerine yazılırsa her x  0,   ve her

için geçerli olan

   x       q  t     t  dt 3  3
(5.3.31)
x
eşitliği elde edilir. (5.3.31) eşitliği  x,   aralığında integrallenirse,


x
s
  x    ds     q  t     t  dt  x  3  3   C2
(5.3.32)
eşitliği elde edilir. Bu eşitliği x   için yazarsak    x  fonksiyonunun (5.3.25)
başlangıç şartını sağladığını da dikkate alırsak,

C2          3  3

(5.3.33)
eşitliği elde edilir. Diğer taraftan   fonksiyonunun tanımı gereği,
    4  4
(5.3.34)
eşitliği sağlanır. (5.3.33) ve (5.3.34) ifadelerinden

C2     4  4   3  3

(5.3.35)
eşitliği elde edilir. (5.3.35) ifadesi (5.3.32) de yerine yazılırsa,


x
s
  x    ds     q  t    t  dt  x  3  3    4   4
(5.3.36)
eşitliği elde edilir. Son eşitlikte integralleme sırası değiştirilirse,



t









ds



q
t

t
dt

dt



q
t

t
ds









     q  t     t  x  t  dt
x s 
 
x x 
 

 x
eşitliği bulunur. Son eşitliği (5.3.36) de yerine yazarsak her x  0,   ve her  
için geçerli olan

  x       q  t     t  x  t  dt  x  3  3    4   4    3  3  (5.3.37)
x
eşitliği (özdeşliği) elde edilir. Böylece    x  çözüm fonksiyonu için (5.3.37)
biçiminde verilmiş integral denklem elde edildi. Bu integral denklemin çözümüne
(yani    x  fonksiyonuna) yakınsayan fonksiyon dizisinin inşa edilmesi için,
integral denklemler teorisinden iyi bilinen ardışık yaklaşma yönteminden
37
yararlanılacaktır. Bu yöntem gereği aşağıdaki rekurrent (ard-arda birbirini üreten)
fonksiyonlar dizisi inşa edilecektir.

0

 x   x  3  3   4  4    3  3 

n
  x     x   
  q  t  
0
n1 
(5.3.38)
t  x  t  dt ,
n  1, 2,...
(5.3.39)
x
M : max q  t 
İlk önce
ve
t0, 
K     max  0   t  gösterimlerinden
t0, 
  x 
yararlanılarak R  0 keyfi sayı olmak üzere
n
fonksiyonlar dizisinin
herhangi kapalı ve sınırlı   R yuvarında




 x     n   x    n1   x 
0
n 1
(5.3.40)
fonksiyonlar dizisinin yakınsaklık durumu incelenecektir. Bu fonksiyonlar dizisi ile
  x 
n
fonksiyonlar dizisinin ya her ikisinin yakınsak ya da her ikisinin ıraksak
oldukları ve de yakınsak oldukları durumda verilmiş (5.3.40) serisinin toplamı ile

n



( x) dizisinin limitinin aynı olduğu açıktır. Bu nedenle  n   x  dizisi yerine
(5.3.40) serisi incelenecektir. Bu serinin terimleri ard arda değerlendirilecektir.

x
x


 x    0   x      q  t   0  t  x  t  dt    R  M  K    x  t  dt
1

1
2
 R  M  K    x    (5.3.41)
2
eşitsizliği bulunur.


x
n
  x     x   
   q  t  
0

n1 
 t  x  t  dt
x
n1
  x     x   
   q  t  
0

n 2 
 t  x  t  dt
ifadelerinden yararlanılarak n  2 için geçerli olan

n
  x  
x
n1
  x   
   q  t   

n1 
t   
n2 
t   x  t  dt
(5.3.42)
eşitliği elde edilir. (5.3.41) eşitsizliğinden ve (5.3.42) eşitliğinden yararlanılarak
(5.3.40) serisinin diğer terimleri değerlendirilecektir. n  2 için
38

x
2
  x     x   
   q  t      t      t   x  t  dt
1
1

0
x
1
2
2
  R  M  K      t     x  t  dt
2

  R  M  K  
2
x  
4
4!
bulunur. Böyle devam ederek tümevarım yöntemi ile
x  
   x     x   R  M  K  
 2n  !
2n
n
n
n1
,
eşitsizliğinin her n  1 için sağlandığı kolayca bulunur.
n=1,2,...
(5.3.43)
x  0,   olduğu için
0   x      2 n olur. Dolayısıyla (5.3.43) ifadesinden
2n
 R  M   2  K   
 n   x    n1   x  
 2n  !
n
eşitsizliği elde edilir.
 R  M   2  K   
K    
 2n  !
n 1
n

sayısal serisi yakınsak olduğundan Weierstrass M-Kriteri gereği (5.3.40) serisi
mutlak ve düzgün yakınsaktır.
  x  fonksiyonlarının
n
(5.3.38) ve (5.3.39)
eşitlikleri ile verilmiş tanımları gereği bu fonksiyonların her biri her x  0,   için
 
:   R bölgesinde analitik olduğundan ve her x  0,   için
  x 
n
dizisi  ( x) fonksiyonuna düzgün olarak yakınsak olduğundan    x  fonksiyonu
da her x  0,   için  değişkeninin tam fonksiyonudur.
5.3.4. Sonuç:    x  fonksiyonu (5.3.1) denklemini ve (5.3.3) sınır şartını
sağlayan ve her x  0,   için  parametresinin tam fonksiyonu olan çözümdür.
5.4. Temel Çözümler ve Karakteristik Fonksiyon
Bu kesimde
 u : u  q  x  u  u , x  0,  
39
(5.4.1)
1 :  1u  0   2u  0     1u  0   2u  0   0
(5.4.2)
 2 :  3u    4u      3u    4u    0
(5.4.3)
sınır değer probleminin özdeğerleri ve özfonksiyonları arasındaki bazı temel
bağıntıları incelenecektir.
u  q  x  u  u,
x  0,  
u  0    2   2

u  0   1  1
(5.4.4)
şartlarından oluşan başlangıç-değer probleminin çözümünü   x  ile,
u  q  x  u  u,
x  0,  
u     4   4

u    3  3
(5.4.5)
şartlarını sağlayan çözümünü    x  ile gösterelim. Bu   x  ve    x  çözüm
fonksiyonları  parametresinin tam analitik fonksiyonlarıdır [14]. Bundan dolayı
W  x,    W  ,  ; x     x    x     x    x 
(5.4.6)
Wronskian determinantı  0,   aralığında x - değişkeninden bağımsız olup [5],
 ’nın tam analitik fonksiyonudur. W  ,  ; x  Wronskian determinantının x
değişkeninden bağımsız olduğu açıktır. Bu nedenle bundan sonra W  x,   yerine
sadece W    yazacağız. Burada özel olarak x  0 yazarsak, bu fonksiyon için
W       x     x     x     x     0     0     0     0 




  2   2    0   1  1    0    2    0    2    0   1   0   1   0 
  N1       N1    
ifadesini, özel olarak x   yazarsak, bu fonksiyon için
W       x     x     x     x                 




    3  3      4   4      3      3      4      4
 N 2     N 2  
ifadesini elde ederiz. Benzer olarak
40



N1    1  0    2  0   1  2   2   2 1  1

 1 2  1 2  1 2  1 2  1 2  1 2
 1



N 2      3       4      3  4   4   4  3   3

 3  4  3  4  3  4  3  4  3  4  3  4
 2
eşitliği bulunur.
5.4.1. Teorem: (5.4.1)-(5.4.3) sınır değer probleminin özdeğerleri ancak ve
ancak W    fonksiyonunun sıfır yerlerinden ibarettir.
İspat: W    nın bir sıfırı 0 olsun. O halde,
W  0   0  x  0  x   0  x  0  x   0
olacaktır. Bu durumda 0  x  ve  0  x  fonksiyonları, diferansiyel denklemler
teorisinde bilinen “ y1 ( x), y2 ( x),..., yn ( x) fonksiyonları n. mertebeden diferansiyel
denklemin lineer bağımsız çözümleri ise, bu fonksiyonların Wronskian determinantı
bütün noktalarda sıfırdan farklıdır.” teoreminin sonucu olarak lineer bağımlıdır. Yani
  x   k   x  ,
0
0
x  0,  
(5.4.7)
olacak şekilde bir k  0 sabiti mevcuttur.
  x  fonksiyonu (5.4.1) denklemini ve (5.4.2) sınır şartını,   x 
0
0
fonksiyonu ise (5.4.1) denklemini ve (5.4.3) sınır şartını sağladığı açıktır. Dolayısıyla
(5.4.7) gereği bu fonksiyonların her biri iki sınır şartını da sağlar. O halde bu
fonksiyonlar (5.4.1)-(5.4.3) sınır değer probleminin çözümü olur. Bu ise   0
sayısının özdeğer olduğunu gösterir.
Şimdi ise   0 sayısının, (5.4.1)-(5.4.3) probleminin özdeğeri olduğunu
kabul ederek, W  0   0 eşitliğinin doğruluğunu ispatlayalım. Herhangi   0
özdeğeri için, W  0   0 olduğu kabul edilsin. O halde 0  x  ve  0  x  çözüm
fonksiyonları lineer bağımsız olur [5]. (5.4.1) denkleminin genel çözümü için
u  x,    C1      x   C2      x 
yazılabilir. Dolayısıyla 0 özdeğerine uygun olan her bir u0  x  fonksiyonu için,
41
u0  x   C1  0  0  x   C2  0  0  x 
olacak şekilde en az biri sıfırdan farklı olan C1 , C2 sayıları bulunur. (5.4.1) eşitliği
ile verilen u0  x  özfonksiyonu (5.4.2)-(5.4.3) sınır şartlarını sağladığından
 1   x   C1   1     x   C2  0
0
0
 2   x   C1   2     x   C2  0
0
0
eşitlikleri geçerlidir. Ci katsayılarının en az biri sıfırdan farklı olduğu için buradan
0 
 1   x    1     x  
0
0
 2   x    2     x  
0
0
(5.4.8)
0
elde edilir. Şimdi bu determinantın elemanları hesaplanırsa   x,   ve   x,  
fonksiyonlarının tanımı gereği,
 1   x     1  0    2  0      1  0    2  0  
0
0
0

0


0




 1  2   2   2 1  1  1  2   2   2 1  1

 1 2  1 2  1 2  1 2  1 2  1 2  1 2  1 2
0
 1     x     1    0    2    0      1   0    2    0  
 1    0    2    0   1   0    2    0 
0
0
0
0
0
0
0
0
0
 N1       N1    
 W   
 2   x     3     4       3     4   
 3     4    3     4  
0
0
0
0
0
0
0
0
0
 N 2      N 2  
 W  
 2     x      3       4         3       4     
0
0

0

0


0



  3  4   4   4 3  3  3  4   4   4  3   3

  3  4  3  4  3  4  3  4  3  4   3  4   3  4   3 4
0
elde edilir. Bulunan bu eşitlikler (5.4.8) determinantında yerlerine yazılırsa,
42
0 
0
W  
W   
0
 0  0   W     W      0  W     0
eşitliği elde edilir. Bu ise W  0   0 kabulüyle çelişir ve teoremin ispatı tamamlanır.
Şimdi ise normalleştirilmiş özelementleri bulalım. W    fonksiyonunun
sıfırlarını n  0,1, 2,... olmak üzere n ile gösterirsek
   x
 n
 n   N1 n

N 
 2 n
 
 


  D  A



eşitliği ile tanımladığımız  n elementleri
An  nn
denklemini sağlar. Dolayısıyla  n ’ler A operatörünün özelementleri olur.
W    fonksiyonunun her n sıfırı için (5.4.6) gereği n  x  ile  n  x 
lineer bağımlı olurlar. O halde her n  0,1, 2,... için
  x   kn  x  ,
n
n
x  0,  
olacak şekilde kn  0 sabiti vardır. A operatörü simetrik olduğu için n  m iken bu
özdeğerlere uygun olan
 n ve  m özelementleri ortogonal olur [31]. Yani
n ,  m  0 dır. O halde A operatörünün  n özelementlerinin normalleştirilmiş
halini
n 
n
n
   x
 n
  N1  n

N 
 2 n
 
 






şeklinde gösterebiliriz.
5.5.   x  ve    x  Çözüm Fonksiyonlarının Asimptotiği
5.5.1. Lemma:   s 2 olmak üzere (5.1.1) diferansiyel denkleminin (5.4.4)
şartını sağlayan çözümü
43
  x     2  s 2  2  cos sx 


x
1
1
1  s 2 1 sin sx   sin s  x  y q  y    y  dy
s
s0
integral denklemini sağlar.
İspat: (5.1.1) diferansiyel denklemini
u  u  qu
(5.5.3)
biçiminde yazdıktan sonra bu denklemi homojen olmayan denklem gibi düşünerek
sabitin değişimi yöntemiyle çözelim. Uygun u  u  0 denkleminin genel çözümü
u  x, s   C1 cos sx  C2 sin sx
biçiminde olduğu için (5.5.3) denkleminin genel çözümünü
u( x, s)  C1 ( x, s) cos sx  C2 ( x, s)sin sx
(5.5.4)
biçiminde arayacağız. Sabitin değişimi yöntemi gereği,
C1  x, s  cos sx  C2  x, s  sin sx  0
C1  x, s  s sin sx  C2  x, s  s cos sx  q  x  u  x, s 
denklem sistemini sağlasınlar. Bu sistemi C1  x, s  ve C2  x, s  değişkenlerine göre
lineer denklem sistemi gibi çözersek,
q  x  u  x, s  sin sx

C1  x, s  
s

C  x, s  q  x  u  x, s  cos sx
 2  
s
(5.5.5)
bulunur. (5.5.5)’den bulduğumuz
x
1
C1  x, s     sin sy q  y  u  y, s  dy  C1
s0
C2  x, s  
x
1
cos sy q  y  u  y, s  dy  C2
s 0
ifadelerini (5.5.4)’de yerine koyarsak,
x
x
1
1
u  x, s    cos sx  sin sy q  y  u  y, s  dy  sin sx  cos sy q  y  u  y, s  dy
s
s
0
0
 C1 cos sx  C2 sin sx
x

1
sin s  x  y  q  y  u  y, s  dy  C1 cos sx  C2 sin sx
s 0
44
(5.5.6)
eşitliğini elde ederiz. (5.1.1) denkleminin (5.4.4) şartını sağlayan çözümünü
aradığımızdan bu şartları kullanırsak
2  s 2 2 
0
1
sin s  0  y  q  y  u  y, s  dy  C1 cos 0  C2 sin 0
s 0
ifadesi elde edilir. Buradan C1  2  s 2 2 bulunur. (5.5.6) ifadesinin türevini alırsak,
x
u  x, s   sin sx  sin sy q  y  u  y, s  dy
0
1
 cos sx sin sx q  x  u  x, s  x  sin s0 q  0  u  0, s  0
s
x
 cos sx  cos sy q  y  u  y, s  dy
0
1
 sin sx cos sx q  x  u  x, s  x  cos s0 q  0  u  0, s  0
s
 sC1 sin sx  sC2 cos sx
x
x
0
0
 sin sx  sin sy q  y  u  y, s  dy  cos sx  cos sy q  y  u  y, s  dy
 sC1 sin sx  sC2 cos sx
elde edilir. Buradan
x
u  x, s    cos s  x  y  q  y  u  y, s  dy  sC1 sin sx  sC2 cos sx
(5.5.7)
0
eşitliğini elde ederiz. Bu ifadede (5.4.4) şartını kullanırsak
0
1  s 2 1   cos s  0  y  q  y  u  y, s  dy  sC1 sin 0  sC2 cos 0
0
ifadesi elde edilir. Buradan C2 
1  s 2 1
bulunur. Bulunan C1 , C2 değerlerini
s
(5.5.6) ve (5.5.7) ifadelerinde yerlerine yazıp gerekli düzenlemeleri yaparsak,



x

1
1
u  x, s    2  s  2 cos sx  1  s 2 1 sin sx   sin s  x  y q  y  u  y , s  dy
s
s0
2




x
u  x, s    s  2  s 2  2 sin sx  1  s 2 1 cos sx   cos s  x  y  q  y  u  y, s  dy
0
integral denklemleri elde edilir. Buradan
  x     2  s 2  2  cos sx 


x
1
1
1  s 2 1 sin sx   sin s  x  y q  y    y  dy
s
s0
yazılabilir ve ispat tamamlanır.
45
5.5.2. Sonuç:   x  çözüm fonksiyonu için
  x     2  s 2  2  cos sx 


x

1
1
1  s 2 1 sin sx   sin s  x  y q  y    y  dy
s
s0



x
  x    s  2  s 2  2 sin sx  1  s 2 1 cos sx   cos s  x  y  q  y    y  dy
0
eşitlikleri sağlanır.
5.5.3. Lemma:   s 2 olmak üzere (5.1.1) diferansiyel denkleminin (5.4.5)
şartını sağlayan çözümü
  x    4  s 4 
2

cos s  x    
3
 s 2 3
s
 sin s  x     1

s x
sin s  x  y q  y     y  dy
integral denklemini sağlar.
İspat: Benzer şekilde ispat edelim. O halde (5.5.5)’den bulduğumuz
C1  x, s  

1
sin sy q  y  u  y, s  dy  C1
s x

1
C2  x, s     cos sy q  y  u  y, s  dy  C2
sx
ifadelerini (5.5.4) de yerine koyarsak,


1
1
u  x, s   cos sx  sin sy q  y  u  y, s  dy  sin sx  cos sy q  y  u  y, s  dy
s
s
x
x
 C1 cos sx  C2 sin sx


1
sin s  x  y  q  y  u  y, s  dy  C1 cos sx  C2 sin sx
s x
(5.5.8)
formülünü elde ederiz. (5.1.1) denkleminin (5.4.5) şartını sağlayan çözümünü
aradığımızdan bu şartları kullanırsak
4  s 2 4  

1
sin s   y  q  y  u  y, s  dy  C1 cos s  C2 sin s
s 
ifadesi elde edilir. Buradan
4  s 2 4  C1 cos s  C2 sin s
bulunur. (5.5.8) ifadesinin türevini alırsak,
46
(5.5.9)

u  x, s    sin sx  sin sy q  y  u  y, s  dy
x
1
+ cos sx sin s q   u  , s     sin sx q  x  u  x, s  x
s

 cos sx  cos sy q  y  u  y, s  dy
x
1
 sin sx cos s q   u  , s     cos sx q  x  u  x, s  x
s
 sC1 sin sx  sC2 cos sx


x
x
  sin sx  sin sy q  y  u  y, s  dy  cos sx  cos sy q  y  u  y, s  dy
 sC1 sin sx  sC2 cos sx
elde edilir. Buradan

u  x, s    cos s  x  y  q  y  u  y, s  dy  sC1 sin sx  sC2 cos sx
(5.5.10)
x
eşitliğini elde ederiz. Bu ifadede (5.4.5) şartını kullanırsak

3  s 2 3   cos s   y  q  y  u  y, s  dy  sC1 sin s  sC2 cos s

ifadesi elde edilir. Buradan
3  s 2 3  sC1 sin s  sC2 cos s
(5.5.11)
bulunur. (5.5.9) ifadesi s cos s ile, (5.5.11) ifadesi sin s ile çarpılıp, taraf tarafa
toplanırsa,



 sC1 cos 2 s  sC1 sin 2 s   s cos s  4  s 2  4  sin s 3  s 2 3





 sC1   s  4  s 2  4 cos s  3  s 2 3 sin s


C1   4  s 2  4 cos s 


1
3  s 2 3 sin s
s
bulunur. Öte yandan, (5.5.9) ifadesi s sin s ile, (5.5.11) ifadesi cos s ile çarpılıp,
taraf tarafa toplanırsa,



sC2 sin 2 s  sC2 cos 2 s  s sin s  4  s 2  4  cos s  3  s 2  3



1
    s   sin s   
s


 s   cos s
sC2  s  4  s 2  4 sin s  3  s 2 3 cos s
C2
2
4
4
47
2
3
3
bulunur. Bulunan C1 , C2 değerlerini (5.5.8) ve (5.5.10) ifadelerinde yerlerine yazıp
gerekli düzenlemeleri yaparsak,




1
3  s 2 3 sin s  x   
s
u  x, s    4  s 2  4 cos s  x    


1
sin s  x  y q  y  u  y, s  dy
s x




u  x, s    s  4  s 2  4 sin s  x     3  s 2 3 cos s  x   

  cos s  x  y q  y  u  y, s  dy
x
integral denklemleri elde edilir. Buradan
  ( x)    4  s 2  4  cos s  x    


1
3  s 2 3 sin s  x   
s


1
sin s  x  y q  y    ( y)dy
s x
yazılabilir ve ispat tamamlanır.
5.5.4. Sonuç:    x  çözüm fonksiyonu için aşağıdaki eşitlikler sağlanır:
  ( x)    4  s 2  4  cos s  x    



1
1
3  s 2 3 sin s  x      sin s  x  y q  y    ( y )dy
s
sx

  ( x)   s   4  s 2  4  sin s  x      3  s 2 3  cos s  x      cos s  x  y q  y    ( y )dy
x
5.5.5. Teorem: 1  0, 2  0, i  0, i  0 (i  1, 4) kabul edelim ve
  s 2 , s    it ile gösterelim. O halde öyle s0  0 vardır ki s  s0 için aşağıdaki
asimptotik eşitlikler sağlanır.
1)  2  0 ise

  ( x)  O  s


 ( x)  O s e t x
2
3

e
tx
(5.5.12)
(5.5.13)
2)  2  0 ise

 ( x)  O s e t x


(5.5.14)

(5.5.15)
 ( x)  O s e t x
48
2
İspat: Önce  2  0 için  ( x) çözüm fonksiyonunun asimptotiğini bulalım.
F1  x  : e
t x
 ( x)
(5.5.16)
ile gösterelim. O halde F1  x  fonksiyonu
F1  x   e
e
e
t x
t x
t x

 1 t x  x
1  s 2 1 


2


s

cos
sx

sin
sx
 2
  e   sin s  x  y q  y    y  dy 
2
s
0


 s

 1x
1  s 2 1 

t y t x
2
sin sx    sin s  x  y q  y  F1  y  e e dy
  2  s  2  cos sx 
s

 s 0

 1x
1  s 2 1 

 t yx
2
sin sx    sin s  x  y q  y  F1  y  e   dy (5.5.17)
  2  s  2  cos sx 
s
s
0


integral denklemini sağlar. (5.5.17) de her iki tarafının mutlak değerini alırsak,
F1  x   e

1
s
e
t x


1
2
2
  2  s  2 cos sx  1  s 1 sin sx 
s


x
 sin s  x  y  q  y 
F1  y  e
 t  y x
dy
0
t x
x

1
1 t  x y
tx
tx
 t yx
2
2
q  y  F1  y  e   dy
  2  s  2 e  1  s 1 e    e
s

 s 0
1
1
  2  s  2  1  s 2 1 
s
s
2
x
 q  y
F1  y  dy
0
eşitsizliğini elde ederiz. Burada
M1    : max F1  x 
(5.5.18)
x0, 
ile gösterirsek, sonuncu eşitsizlikten
M1      2  s 2  2 

1
1
1  s 2 1  M1     q  y  dy
s
s
0
eşitsizliği elde edilir. Buradan ise

1
M1    1 
s



0



1
1
1
2
q  y  dy   s   2  1  2  2  3 1 


s
s
s



eşitsizliği bulunur. O halde

s  2 q  y  dy : r0
0
49
(5.5.19)
için

1
1
1
2
M1     2 s   2  1  2  2  3 1 
r0
r0
r0


M1     M 0 s
2
(5.5.20)
bulunur. Burada


1
1
1
M 0  2   2  1  2  2  3 1 
r0
r0
r0


dır. Dolayısıyla r0  0 sayısı (5.5.19) ile tanımlanmak üzere s  r0 için (5.5.16),
(5.5.18) ve (5.5.20)’den
 ( x)  M 0 s e t x
2
(5.5.21)
eşitsizliği elde edilir. Buradan ise

 ( x)  O s e t x
2

yazılır ve (5.5.12) eşitliği ispatlanmış olur.
Şimdi (5.5.13) eşitliğinin doğruluğunu ispatlayalım. (5.5.21) eşitsizliği ve
Sonuç 5.5.2. gereğince s  r0 için

  x   s  2  s  2 e  1  s 1 e   e t  x  y  q  y    y  dy
2
tx
tx
2
0



 s  2  s 2  2  1  s 2 1 e   e
tx
t  x y
q  y  M 0 s e dy
2
ty
0


 3 tx
1
1
1
2 tx
   2  1  2  2  3 1  s e  s e M 0  q  y  dy


s
s
s
0




 3 tx
M
1
1
1
   2  1  2  2  3 1  0  q  y  dy  s e
r0
r0
r0
r0 0


M
M r  3 tx
 0  0 0  s e
r0 2 
 2
ifadesinden
  x   M 0 s e t x
3
eşitsizliği elde edilir. Buradan ise

  ( x)  O s e t x
50
3

yazılır ve (5.5.13) eşitliği ispatlanmış olur.  2  0 durumu için, (5.5.14) ve (5.5.15)
eşitlikleri de benzer şekilde ispatlanır.
5.5.6. Teorem: 1  0, 2  0, i  0, i  0 (i  1, 4) kabul edelim ve
  s 2 , s    it ile gösterelim. O halde öyle s0  0 vardır ki s  s0 için aşağıdaki
asimptotik eşitlikler sağlanır.
1)  4  0 ise

  ( x)  O  s
 ( x)  O s e t  x  
2
3

e
t  x  


(5.5.22)
(5.5.23)
2)  4  0 ise

 ( x)  O s e t  x  


(5.5.24)

(5.5.25)
 ( x)  O s e t  x  
2
İspat: Önce  4  0 için  ( x) çözüm fonksiyonunun asimptotiğini bulalım.
F2  x  : e
 t  x  
  ( x)
(5.5.26)
ile gösterelim. O halde F  x  fonksiyonu
F2   x   e
 t  x  
1


2
2
  4  s  4 cos s  x     s 3  s 3 sin s  x    






1  t x  
 e     sin s  x  y q  y    ( y )dy 
s
x

e
 t  x  
1


2
2
  4  s  4 cos s  x     s 3  s 3 sin s  x    





1
t y   t x 
  sin s  x  y q  y  F2   y  e  e   dy
s0
e
 t  x  
1


2


s

cos
s
x



3  s 2 3 sin s  x    


4
4

s




x
1
 t x y
  sin s  x  y q  y  F2   y  e   dy
s0

(5.5.27)
integral denklemini sağlar. Bu durumda (5.5.27) eşitliğinin her iki tarafının mutlak
değerini alırsak,
51
F2   x   e

1
s
e
 t  x  


1
2
2
  4  s  4 cos s  x     3  s 3 sin s  x    
s



 sin s  x  y  q  y 
F2   y  e
 t  x y
dy
x

1
t  x  
t x  
2
 3  s 2 3 e   
 4  s 4 e
s


 t  x  


1 t  x y
 t x y
e
q  y  F2   y  e   dy

s x
1
1
  4  s  4  3  s 2 3 
s
s
2

 q  y
F2   y  dy
x
eşitsizliğini elde ederiz. Burada
Y1    : max F2  x 
(5.5.28)
x0, 
ile gösterirsek, sonuncu eşitsizlikten
Y1      4  s 2  4 

1
1
3  s 2 3  Y1     q  y  dy
s
s
0
eşitsizliği elde edilir. Buradan ise

1
Y1    1 
s



0



1
1
1
2
q  y  dy   s   4  3  2  4  3 3 


s
s
s



eşitsizliği bulunur. O halde

s  2 q  y  dy : r0
(5.5.29)
0
için

1
1
1
2
Y1     2 s   4  3  2  4  3 3 
r0
r0
r0


Y1     Y0 s
2
(5.5.30)
bulunur. Burada


1
1
1
Y0  2   4  3  2  4  3 3 
r0
r0
r0


dır. Dolayısıyla r0  0 sayısı (5.5.29) ile tanımlanmak üzere s  r0 için (5.5.26),
(5.5.28) ve (5.5.30)’den
52
 ( x)  Y0 s e t  x 
2
(5.5.31)
eşitsizliği elde edilir. Buradan ise

 ( x)  O s e t  x  
2

yazılır ve (5.5.22) eşitliği ispatlanmış olur.
Şimdi (5.5.23) eşitliğinin doğruluğunu ispatlayalım. (5.5.31) eşitsizliği ve
Sonuç 5.5.4. gereğince s  r0 için

  ( x)  s  4  s 2  4 e t  x    3  s 2 3 e t  x     e t  x  y  q  y    ( y )dy
0


 s  4  s 2  4  3  s 2 3 e
t  x  

 e
t  x y
q  y  Y0 s e
2
t  y  
dy
0


 3 t  x  
1
1
1
2 t  x  
   4  3  2  4  3 3  s e
s e
Y0  q  y  dy


s
s
s
0




 3 t x 
Y
1
1
1
   4  3  2  4  3 3  0  q  y  dy  s e  
r0
r0
r0
r0 0


 Y Y r  3 t x 
 0  0 0  s e  
 2 r0 2 
ifadesinden
 ( x)  Y0 s e t  x  
3
eşitsizliği elde edilir. Buradan ise

 ( x)  O s e t  x  
3

yazılır ve (5.5.23) eşitliği ispatlanmış olur.  4  0 durumu için, (5.5.24) ve (5.5.25)
eşitlikleri de benzer şekilde ispatlanır.
5.5.7. Teorem: 1  0, 2  0, i  0, i  0 (i  1, 4)
kabul edelim ve
  s 2 , s    it ile gösterelim. O halde öyle s0  0 vardır ki s  s0 için aşağıdaki
asimptotik eşitlikler sağlanır.
1)  2  0 ise

  x   s 2 2 cos sx  O s e t x

  x   s3 2 sin sx  O s e t x
53
2


(5.5.32)
(5.5.33)
2)  2  0 ise
 
   x   s  cos sx  O  s e 
  x   s1 sin sx  O e t x
tx
2

(5.5.34)
(5.5.35)
1
İspat:  2  0 olsun. (5.5.21) ifadesini, Sonuç 5.5.2. deki
 ( x) çözüm
fonksiyonunun integral kısmında dikkate alırsak, yeteri kadar büyük s ’ler için
x
x
 sin s  x  y q  y    y  dy   sin s  x  y  q  y    y  dy  M 0 s
0
x
2
e
0
t  x y
q  y  e dy
ty
0

 M0 s e
2
tx
 q  y
0
eşitliğini elde ederiz. Buna göre
 sin s  x  y q  y   y  dy  O  s
x
2
e
tx

0
asimptotik eşitliği sağlanır. Bunu Sonuç 5.5.2. deki  ( x) ifadesinde dikkate alırsak,
(5.5.32) ifadesini elde ederiz. (5.5.33) ifadesi (5.5.32)’ye benzer şekilde ispatlanır.
 2  0 için, (5.5.34) ve
(5.5.35) eşitlikleri,  4  0 durumuna benzer şekilde
ispatlanır.
5.5.8. Teorem: 1  0, 2  0, i  0, i  0 (i  1, 4) kabul edelim ve
  s 2 , s    it ile gösterelim. O halde öyle s0  0 vardır ki s  s0 için aşağıdaki
asimptotik eşitlikler sağlanır.
1)  4  0 ise

 ( x)  s 2 4 cos s  x     O s e t  x 


 ( x)  s3 4 sin s  x     O s e t  x 
2
(5.5.36)

(5.5.37)
2)  4  0 ise

 ( x)  s3 sin s  x     O e t  x 


 ( x)  s 2 3 cos s  x     O e t  x 
54
(5.5.38)

(5.5.39)
 ( x) çözüm
İspat:  4  0 olsun. (5.5.31) ifadesini, Sonuç 5.5.4. deki
fonksiyonunun integral kısmında dikkate alırsak, yeteri kadar büyük s ’ler için

 sin s  x  y q  y  


( y )dy   sin s  x  y  q  y    ( y ) dy  Y0 s
x
x
2
x
e
t  x y
q  y e
t  y  
dy
0
 Y0 s e
2
t  x  

 q  y
0
eşitliğini elde ederiz. Buna göre
 sin s  x  y q  y   y  dy  O  s
x
2
e
t  x  

0
eşitliği sağlanır. Bunu Sonuç 5.5.4. deki  ( x) ifadesinde dikkate alırsak, (5.5.36)
ifadesini elde ederiz. (5.5.37) ifadesi (5.5.36)’ye benzer şekilde ispatlanır.  4  0
için, (5.5.38) ve (5.5.39) eşitlikleri,  4  0 durumuna benzer şekilde ispatlanır.
5.6.   x  ve    x  Fonksiyonlarının Wronskianının Asimptotiği
5.6.1. Teorem: W    için aşağıdaki asimptotik formüller geçerlidir.
1) 2  0 , 4  0 ise

W     s5 2 4 sin s  O s e

t
4
2) 2  0 , 4  0 ise

W     s 4 14 cos s  O s e
3
t

3) 2  0 , 4  0 ise

3

2
t

t

W     s 4 2 3 cos s  O s e
4) 2  0 , 4  0 ise
W     s3 13 sin s  O s e
İspat:
W        3     4     3     4
olduğunu daha önceden biliyoruz.
55
(5.6.1)
1) 2  0 , 4  0 olduğu durumunu araştıralım.   s 2 olduğunu dikkate
alarak (5.5.32) ve (5.5.33) asimptotik eşitliklerini (5.6.1) eşitliğinde yerine yazarsak


W     s 2  s 2  2 cos s  O s e


  s 2  2 cos s  O s e
t
 
3

    s  sin sx  O  s
t

 s 2 s 3  2 sin sx  O s e
3
3
2
2
2
e
tx
tx
 
 
4
4
eşitliği elde edilir. Buradan
   s   sin s  O  s
 s   cos s  O  s e   s   sin s  O  s
W      s 4  2 3 cos s  O s 3 e
t
5
2
t
2
2
3
3
2

  s 5  2  4 sin s  O s e
4
4
4
2
4
e
e
t
t

t


bulunur.
2) 2  0 , 4  0 durumunu araştıralım.   s 2 olduğunu dikkate alarak
(5.5.34) ve (5.5.35) asimptotik eşitliklerini (5.6.1) eşitliğinde yerine yazarsak


W     s 2  s1 sin s  O s e


1
1
  s1 sin s  O s e
   s  s  cos s  O  s e  
    s  cos s  O  s e  
t
2
t
t
2
3
1
4
t
2
3
1
4
eşitliği elde edilir. Buradan

W      s 3 13 sin s  O s e

 s   cos s  O  s
1
t
1
4
3
e
4
1
 s13 sin s  O s e
4
s  
t
t

cos s  O s e
3
t

  s   cos s  O  s e 
t
2
1

4
4
bulunur.
3) 2  0 , 4  0 durumunu araştıralım. Bu durumda  4  0 olduğu için
W    fonksiyonu
W        3     3      4
şeklinde ifade edilir. Buradan
56


W     s 2  s 2  2 cos s  O s e


 s 3  2 sin sx  O s e
2


  s   cos s  O  s
2
3
2
3
2
3
e
2

cos s  O s e
t
 
3
4
  s   cos s  O  s e 
t
 s 3  2  4 sin s  O s e
4
     s 
 
tx
=  s 4  2 3 cos s  O s 3 e
t
t
2
2
t
t
3


eşitliği elde edilir.
4) 2  0 , 4  0 durumunu araştıralım. Bu durumda W    fonksiyonu
   s  sin s  O  s
 s   cos s  O  s e 
W      s 3 13 sin s  O s e
t
1
3
1
e
t

t
2
1
4

  s 3 13 sin s  O s e
2
t

şeklinde ifade edilir.
5.7. Green Fonksiyonunun Kurulması
Öncelikle ele aldığımız problemdeki sınır şartlarını
     u  0   
1

3
1

2
 2 u  0 

(5.7.1)

(5.7.2)

 3 u    4  4 u  
şeklinde yazalım. Özdeğerlerden farklı her  
kompleks sayısı için (5.5.3)
diferansiyel denkleminin  ( x) ve  ( x) çözümleri lineer bağımsız olduklarından
bu denklemin genel çözümünü
u  x,    C1     ( x)  C2     ( x)
şeklinde yazabiliriz. Sabitin değişimi yöntemini kullanarak
u  x   q  x  u  x   u  f  x 
(5.7.3)
denkleminin genel çözümünü
u  x,    C1  x,    ( x)  C2  x,    ( x)
şeklinde arayalım. Sabitin değişimi yöntemi gereği
C1  x,    ( x)  C2  x,    ( x)  0
57
(5.7.4)
C1  x,    ( x)  C2  x,    ( x)  f  x 
denklem sistemini sağlasınlar. Bu sistemden
   ( x) f  x 
C1  x,   
W  
C2  x,   
 ( x) f  x 
W  
elde edilir. Bu ifadelerden bulduğumuz
C1  x,    
C2  x,   

1
W    x
1
x
W    0
  ( y ) f  y  dy C1   
 ( y) f  y  dy  C2   
ifadelerini (5.7.4)’de yerlerine koyarsak,
 1 

u  x,     ( x) 
  ( y ) f  y  dy  C1    

W    x

 1 x

  ( x) 
 ( y ) f  y  dy  C2    

W    0

 ( x) 
  ( x) x
u  x,   
  ( y ) f  y  dy 
 ( y ) f  y  dy
W    x
W    0
(5.7.5)
 C1     ( x)  C2      ( x)
u   x,   





(
x
)
     ( y ) f  y  dy   ( x)   ( x) f  x  
W   
x

1
x




(
x
)
    ( y) f  y  dy   ( x)   ( x) f  x  
W   
0

 C1     ( x)  C2      ( x)


1
 ( x) 
  ( x) x

(
y
)
f
y
dy

 ( y ) f  y  dy
 

W    x
W    0
(5.7.6)
 C1     ( x)  C2      ( x)
elde edilir. Bulunan (5.7.5) ve (5.7.6) ifadeleri (5.7.1) sınır şartında yerlerine
yazılırsa
58

  (0) 

1  1 

(
y
)
f
y
dy

C


(0)

C


(0)








1

2


W    0


   (0) 

  2   2  
  ( y ) f  y  dy  C1     (0)  C2      (0) 

W    0



olur. (5.4.4) eşitlikleri kullanılırsa


  2   2
1  1 
 W  






0


  ( y) f  y  dy  C1      2   2   C2      (0)
 1  1
  2   2 
 W  






0  ( y) f  y  dy  C1    1  1  C2      (0) 




yazılır. Buradan
         C           (0)C   
          C            (0)C   
      (0)         (0)  C     0


1
1
2
2
2
1
2
1

1
1
1
1
1
2

1
2

2
2
2

2
2
bulunur. Burada
      (0)   
1
1

2

 2  (0)  W     0
olduğundan
C2     0
elde edilir. Benzer şekilde (5.7.5) ve (5.7.6) ifadeleri (5.7.2) sınır şartında yazılırsa

   ( ) 

3  3 

(
y
)
f
y
dy

C


(

)

C


(

)








1

2


 W    0


   ( ) 

  4   4  
 ( y ) f  y  dy  C1     ( )  C2      ( ) 

 W    0



olur. (5.4.5) eşitlikleri kullanılırsa

  4   4 



 ( y ) f  y  dy  C1     ( )  C2     4   4 
3
3 


 W    0



   3 
  4   4  3
  ( y) f  y  dy  C1    ( )  C2    3  3
 W    0



yazılır. Buradan
59



     ( )C              C   
        ( )C              C   
      ( )         ( )  C     0


3

3
4
1

4
3
3
3
3
1
4

4


4
4
4
4

3
2
3
2
1
bulunur. Burada

3

 3  ( )  4  4  ( )  W     0
olduğundan
C1     0
elde edilir. O halde (5.7.3) denkleminin (5.7.1), (5.7.2) sınır şartlarını sağlayan
çözümü için
u  x,   
 ( x) 
  ( x) x

(
y
)
f
y
dy

 ( y ) f  y  dy
 

W    x
W    0
(5.7.7)
formülü bulunur. Burada
   ( x) ( y )
, 0 y  x 
 W  

G  x, y ,    
 ( x)   ( y ) , 0  x  y  
 W   
(5.7.8)
olarak alırsak, (5.7.7) eşitliği

u  x,     G  x, y,   f  y  dy
0
şeklinde yazılır. Bu şekilde (5.1.1)-(5.1.3) sınır değer probleminin Green fonksiyonu
(5.7.8) şeklinde olur.
5.8. Özdeğerler İçin Asimptotik Formlar
Bu bölümde özdeğerlerin asimptotik açılımının ilk iki terimini bulacağız.
Bunun için ilk olarak W    fonksiyonunun sıfır yerlerinin asimptotik davranışlarını
inceleyeceğiz. Daha sonra Teorem 5.6.1 de olduğu gibi dört durum için ayrı ayrı
araştıracağız.
60
Teorem 5.8.1.
(5.1.1)-(5.1.3) sınır değer probleminin özdeğerleri için
aşağıdaki asimptotik formüller geçerlidir.
1) 2  0, 4  0 durumu için
1
sn   n  2   O  
n
2) 2  0, 4  0 durumu için
3

1
sn   n    O  
2

n
3) 2  0, 4  0 durumu için
3

1
sn   n    O  
2

n
4) 2  0, 4  0 durumu için
1
sn   n  1  O  
n
İspat:
1) 2  0, 4  0 ise

W     s5 2 4 sin s  O s e
4
t

asimptotik ifadesini

W1     s5 2 4 sin s ve W2     O s e
4
t

olmak üzere
W     W1     W2   
şeklinde gösterebiliriz. Kompleks s -düzleminde s    it olmak üzere


1
1


 s    n   , t   n   , n  0,1, 2,...
2
2




bölgesinin sınırını  n ile gösterelim.
W1    
1
5
2 4 s e t  , t  
2

W2     O s e
4
61
t
 , s 
olduğundan, yeteri kadar büyük n
sayıları için  n üzerinde W1     W2   
olduğu görülür. O halde Rouche Teoremi gereği  n eğrisi içinde W   
fonksiyonunun sıfır yerlerinin sayısı n  2 olmak üzere, 2  n  1  6 olduğu açıktır
 0,0,0,0,0,0, 1,1, 2, 2,...,   n  2 ,  n  2 ,... .
W1     W1  s 2  fonksiyonu çift fonksiyon olduğu için sadece pozitif reel
eksen üzerindeki sıfır yerlerini incelemek yeterli olacaktır. Bu sıfır yerlerini
s0  s1  s2  0, s3  1, s4  2, ... , sn  n  2, ...
n  2,3, 4,...
şeklinde sıralayabiliriz.  n1 eğrisi ile  n eğrisi arasında kalan bölgede 2 tane sıfır
yeri mevcuttur. Rouche Teoremini uygulayarak, n  n0 için pozitif reel eksenin bu
bölgede kalan
n
3
1
 s  n
2
2
aralığında tek bir tane sn sıfır yeri bulunur. Buradan
sn   n  2  
1
2
elde edilir.
 n  sn   n  2 
şeklinde ifade edersek
n 
1
2
(5.8.1)
olur. Böylece
sn   n  2    n
eşitliğini elde etmiş oluruz. sn sayılarının W1    fonksiyonunun sıfır yerleri
olduğunu dikkate alarak W     0 eşitliğinde s yerine sn yazarsak,
  n  2    n  2 4 sin  n  2     n   O  n4 
5
asimptotik eşitliği bulunur. Buradan
1
sin  n  2     n   O  
n
62
1
sin  n  O  
n
eşitliğini elde ederiz. Bu eşitlikten ve (5.8.1) gereği,
1
n  O  
n
bulunur. Buradan
1
sn   n  2   O  
n
asimptotik eşitliğini elde ederiz. Benzer ispat diğer durumlar için de yapılabilir.
Lemma 5.8.2. (5.1.1) diferansiyel denkleminin (5.3.5) ve (5.3.6) şartlarını
sağlayan   x  çözümü için
1)  2  0 ise
x
s
2
  x   s 2  2 cos sx  s1 sin sx   2 sin sx  q  y  dy  O 1
 '  x   s3  2 sin sx  s 2 1 cos sx 
0
x
s2
 2 cos sx  q  y  dy  O  s 
2
0
2)  2  0 ise
1
1
  x   s1 sin sx   2 cos sx  1 cos sx  q  y  dy  O  
2
s
0
x
x
s
   x   s 1 cos sx  s 2 sin sx  1 sin sx  q  y  dy  O 1
2
0
'
2
asimptotik ifadeleri sağlanır.
İspat:
1)  2  0 ise
(5.1.1)-(5.1.3) sınır değer probleminin özdeğerleri reel sayı olduğundan lms  t  0
olur. Böylece (5.5.32) asimptotik formülünden
  x   s 2 2 cos sx  O  s 
yazılır. 5.7.2 asimptotik ifadesini Lemma 5.5.1 de yerine yazarsak
63
(5.8.2)
  x     2  s 2  2  cos sx 


x

x
1
1
1  s 2 1 sin sx    s 2  2 cos sy sin  sx  sy  q  y  dy
s
s0
x
1
  sin  sx  sy  q  y  O  s  dy
s0



1
1
  2  s  2 cos sx  1  s 2 1 sin sx   s 2  2 cos sy sin sx cos syq  y  dy
s
s0
2
x
x
1
1
  s 2  2 cos sy sin sy cos sxq  y  dy   sin sx cos syq  y  O  s  dy
s0
s0
x
1
  sin sy cos sxq  y  O  s  dy
s0



x

1
  2  s  2 cos sx  1  s 2 1 sin sx  s 2 sin sx  cos sy cos syq  y  dy
s
0
2
1
 s 2 cos sx  cos sy sin syq  y   O  
s
0
x
x
  2 cos sx  s  2 cos sx  s1 sin sx  s 2 sin sx  cos sy cos syq  y  dy
2
0
1
 s 2 cos sx  cos sy sin syq  y  dy  O  
s
0
x
buluruz.
1
1
0 sin sy cos syq  y  dy  2 0 sin 2syq  y  dy  O  s 
x
x
1
1
1
0 cos syq  y  dy  2 0 1  cos 2sy  q  y  dy  2 0 q  y  dy  O  s 
x
x
x
2
ifadelerini son bulduğumuz   x  ifadesinde yerine yazarsak
2
s
2
  x   s 2  2 cos sx  s1 sin sx   2 sin sx  q  y  dy  O 1
0
asimptotiğini elde ederiz. (5.8.2) ifadesini Sonuç 5.5.2 deki  '  x  de yerine
yazarsak
x
 '  x   s   2  s 2  2  sin sx   1  s 2 1  cos sx   cos s  x  y  q  y    y  dy
0
64



x

  s  2  s 2  2 sin sx  1  s 2 1 cos sx    s 2  2 cos sy cos  sx  sy  q  y  dy
0
x
  cos  sx  sy  q  y  O  s  dy
0



x

  s  2  s 2  2 sin sx  1  s 2 1 cos sx   s 2  2 cos sy cos sx cos syq  y  dy
0
x
x
0
0
  s 2  2 cos sy sin sx sin syq  y  dy   cos sx cos syq  y  O  s  dy
x
  sin sx sin syq  y  O  s  dy
0



x

  s  2  s  2 sin sx  1  s 1 cos sx  s  2 cos sx  cos sy cos syq  y  dy
2
2
2
0
x
x
0
0
 s  2 sin sx  cos sy sin syq  y  dy  cos sx  cos syq  y  O  s  dy
2
x
 sin sx  sin syq  y  O  s  dy
0
x
s2
 s  2 sin sx  s 1 cos sx   2 cos sx  q  y  dy  O  s 
2
0
3
2
asimptotiğini elde ederiz.
2)  2  0 durumu için aynı yöntem takip edilerek
1
 
x
1
  x   s1 sin sx   2 cos sx  1 cos sx  q  y  dy  O  
2
s
0
s
2
x
 '   x   s 2 1 cos sx  s 2 sin sx  1 sin sx  q  y  dy  O 1
0
asimptotik ifadelerini elde ederiz.
Teorem 5.8.3. (5.1.1)-(5.1.3) sınır değer probleminin özdeğerleri için
aşağıdaki asimptotik formüller geçerlidir.
1) 2  0, 4  0 ise

 
C
1  1 1
 1 
sn   n  2  
 O  2  , C     q  y  dy  3 
  2 2 0
4 
 n  2  n 
65
2- 2  0, 4  0 ise

 
3
D
1  3 1

 1 
sn   n   
 O  2  , D     q  y  dy  2 
3
2 
  4 2 0
1 

n 
n 
2

3) 2  0, 4  0 durumu için

 
3
E
1 1

 1 
sn   n   
 O  2  , E   1   q  y  dy  4 
3
2 
  2 2 0
3 

n 
n 
2

4) 2  0, 4  0 durumu için
sn   n  1 

 
F
1 1
 1 
 O  2  , F   2   q  y  dy  4 
  1 2 0
3 
 n  1  n 
İspat:
1) 2  0, 4  0 ise
W        3   '   4     3   '   4
eşitliğinde

s
2
    s 2  2 cos s  s1 sin s   2 sin s  q  y  dy  O 1
0

2
s
     s  2 sin s  s 1 cos s   2 cos s  q  y  dy  O  s 
2
0
'
3
2
ifadeleri yerlerine yazılırsa

 
s3
2
W     s 3  2 cos s  s 13 sin s   2 3 sin s  q  y  dy  O s
2
0
4
3

 
s4
s  2  4 sin s  s 1 4 cos s   2  4 cos s  q  y  dy  O s 3
2
0
5
4

s
s 2  2 3 cos s  s13 sin s   2 3 sin s  q  y  dy  O 1
2
0
s3  2  4 sin s  s 2 1 4 cos s 

s2
 2  4 cos s  q  y  dy  O  s 
2
0
s 4  2 3 cos s  s5  2  4 sin s  s 4 1 4 cos s 
elde edilir. Bu ifadeyi s5  2  4 ye bölersek
66

 
s4
3
 2  4 cos s  q  y  dy  O s
2
0


1 3
1 1
1
 1 
cos s  sin s 
cos s  cos s  q  y  dy  O  2   0  W   
s 4
s 2
2s
s 
0
  1

1
1
sin s  cos s  1  3   q  y  dy   O  2 
s
s 
 2 4 2 0

bulunur.
S  Sn ,
1
Sn   n  2   O   ,
n
1
n  O  
n
olduğundan


1
 1  
 1  
0  sin   n  2   O      
cos   n  2   O     
 n   n  2  O  1 
 n  


   
n
 1 3 1 

 1 
    q  y  dy   O  2 
n 
 2 4 2 0

1
1
 sin  n  2   cos O     cos  n  2   sin O   
n
n

1 
1
1 
cos  n  2   cos O     sin  n  2   sin O    

 n  2 
n
n 
 1 3 1 

 1 
    q  y  dy   O  2 
n 
 2 4 2 0



1 
1
 1    1 3 1
1
sin O    
cos
O



q  y  dy   O  2 

  

n2 
n
 n    2 4 2 0
n 

sin  n 
  1

1
1
cos  n  1  3   q  y  dy   O  2 
n2
s 
 2 4 2 0

cos  n 1 cos  n 3 cos  n 
1
sin  n 


q  y  dy O  2 

n  2 2
n  2 4 2  n  2 0
s 
1
1
1
1 O  2 
1 O  2 
1 O  2  
1
1
 n  1
 n  3
n 
 n  O  3  


qdy O  2 

n2
n2
2  n  2 0
2
4
n 
s 

1 1
1 3
1
1
1
 n  O  3  


qdy O  2 

 n  n  2 2 n  2 4 2  n  2 0
s 
67
 n 


1  1 3 1
1


qdy   O  2 


n  2  2 4 2 0
n 

şeklinde bulunur.  n  sn   n  2  olduğundan
Sn 


1
1  1 3 1
 1 
n

2




qdy   O  2  





 
n  2  2 4 2 0
 n  

C
 1
Sn   n  2  
 O 2 ,
 n  2  n 


1  1 3 1
C      qdy 
  2 4 2 0

elde edilir. Teoremin 2., 3., ve 4. durumları için de aynı yöntem takip edilerek ispat
yapılabilir.
68
6. SONUÇLAR ve ÖNERİLER
Yüksek lisans tez çalışmamızda
 u : u  q  x  u  u
Sturm-Liouville denkleminden ve
 1u  0   2u  0     1u  0   2u  0 
  3u( )  4u( )    3u( )   4u( ) 
sınır şartlarından oluşan sınır değer problemine ait Hilbert uzayı oluşturulmuş,
probleme uygun operatörün simetrikliği gösterilmiş, çözüm fonksiyonlarının
asimptotiği ve bunlardan yararlanarak karakteristik fonksiyonun asimptotiği
bulunmuştur. Ayrıca Green fonksiyonu elde edilmiş ve son bölümde özdeğerlerin
asimptotik açılımı incelenmiştir. Burada q  x  ,
0,  
aralığında sürekli bir
fonksiyondur.
Bu çalışmada dikkat çeken özellik ise hem denklemde hem de sınır
şartlarında  özdeğer parametresinin bulunmasıdır. Ayrıca tezde bulunan sonuçlar
orijinal olup, giriş bölümünde de belirttiğimiz gibi fiziğin birçok somut
problemlerinin analitik ve yaklaşık çözümlerinin bulunmasında da uygulanabilir.
İleriye dönük çalışmalar olarak bu tip problemlerin çalışıldığı aralıkta bir ya
da daha fazla noktada süreksiz olması durumuna göre yeni çalışmalar yapılabilir.
69
KAYNAKLAR
1. Bayraktar, M. Analiz, Nobel Yayın No: 1601, 1. Basım, Ankara, 2010.
2. Binding, P. A.; Browne P. J.; Watson, B. A. Sturm-Liouville Problems with
Boundary Conditions Rationally Dependent on The Eigenparameter II, Journal of
Computational and Applied Matematics, 148, 2002, 147-169.
3. Birkhoff, G. D. On The Asymptotic Character of The Solution of The
Certain Linear Differential Equations Containing Parameter, Trans. Amer. Math.
Soc., Vol.9 1908, pp. 219 – 231.
4. Birkhoff, G. D. Boundary Value and Expantion Problems of Ordinary
Linear Differential Equations, Trans. Amer. Math. Soc., Vol. 9 1908, pp. 373 – 395.
5. Boyce, W. E.; Diprima, R. C. Elementary Differential Equations and
Boundary Value Problems, John Willey and Sons, New York, 1977, pp. 544-554.
6. Çağlıyan M.; Çelik N.; Doğan S. Adi Diferansiyel Denklemler, Dora
Yayın No:6, 2. Baskı, Bursa. 2008.
7.
Dunford, N.; Schwartz, J. T. Linear Operators II, Spectral Theory,
Interscience, New York, 1963.
8. Fulton, C. T. Two-point Poundary Value Problems with Eigenvalue
Parameter Contained in The Boundary Condition, Proceedings of the Royal Society
of Edinburgh. Section A 77, 1977, p. 293-308.
9. Gohberg, I. C.; Krein, M. G. Introduction to The Theory of Linear NonSelfadjoint Operator, Amer, Math. Soc., Providence, 1969.
10. Hinton, D. B. An Expansion Theorem for Eigenvalue Problem with
Eigenvalue Parameter in The Boundary Condition, Quart. J. Math. Oxford, vol. 30,
No: 2, 1979, 33-42.
70
11. Kapustin, N. YU.; Moiseev E. I. On Spectral Problem in The Theory of
Parabolohyoperbolic Heat-transfer Equation, Doklady Akademi Nauk SSSR 352,
no. 4 1997, 451-454 (in Russian).
12. Kerimov, N. B.; Mamedov, Kh. K. On a Boundary Value Problem with a
Spectral Parameter in The Boundary Conditions, Sibirsk. Math. J. 40, No:2, 1999,
281-290.
13. Kreyszing, E. Introductory Functional Analysis with Applications, New
York, 1978.
14. Levitan, B. M.; Sarqsyan, I.S. Sturm-Liouville ve Direkt Operatörler,
Moskova, Nauka, (Rusca), 1988.
15. Marçenko, V. A. Sturm-Liouville Operatörünün Spektral Teorisi, Kiev,
Naukova Dumka, (Rusca), 1972.
16. Markushevich, A. I. Introduction to Analytic Functions Theory I, II,
Moskow, 1977.
17. Naimark, M. A. Linear Differantial Operators, Ungar, New York, 1967.
18. Rasulov, M. L. Methods of Contour Integration, Amsterdam: North
Holland Publishing Company, 1967.
19. Russakovskiy, E. M. Sınır Şartları Polinom Biçiminde Özdeğer
Parametresi İçeren Sınr Değer Probleminin Operatör Yorumu, Funk. Analizi eko
priloj. 9 No:4, 1975, 91-92 (Rusca).
20. Schneider, A. A Note Eigenvalue Problems with Eigenvalue Parameter in
The Boundary Conditions, Math. Z. 136, 1974, 163-167.
21. Shkalikov, A. A. Boundary Value Problems for Ordinary Differential
Equations with a Parameter in Boundary Conditions, Trudy., Sem., Imeny,
I.G.Petrovsgo, 9, 1983, 190-229
71
22. Smirnov, V. I. A Course of Higher Mathematics, Part 5, Pergaman Pres,
Oxford, 1964.
23. Tamarkin, J. D. Some General Problems of The Theory of Ordinary
Linear Differantial Equations and Expansions of an Arbitrary Function in Series of
Fundamental Functions, Math. Z. 27, 1928, 1 – 54.
24. Uluçay, C. Fonksiyonlar Teorisi ve Riemann Yüzeyleri, A.Ü. Fen
Fakültesi, Ankara, 1971.
25. Titchmarsh, E. C. Eigenfunction Expansions Associated with Second
Order Differential Equations, 2nd end, Oxford Univ. Pres, London, 1962.
26. Triebel, H. Interpolation Theory ve Riemann Yüzeyleri, A.Ü., Fen
Fakültesi, Ankara, 1978.
27. Walter, J. Regular Eigenvalue Problems with Eigenvalue Parameter in
The Boundary Conditions, Math. Z., 133, 1973, 301-312.
28. Yakubov, S. Completeness of Root Functions of Regular Differential
Operators, Longman, Scientific, Technical, 1994.
29. Yakubov, S.; Yakubov, Y. Abel Basis of Root Functions of Regular
Boundary Value Problems, Math. Nachr. 197, 1999, 157-187
30. Yakubov, S.; Yakubov, Y. Differential Operator Equations (Ordinary
and Partial Differantial Equations), Chapman and Hall/CRC, Boca Raton, 2000.
31. Yosida, K. Functional Analisis, Springer-Varlag. Berlin, 1965.
72
ÖZGEÇMİŞ
1987 yılında Kahramanmaraş’ta doğan Yasemin KUZU, ilk ve orta öğrenimini
sırasıyla Kadirli İlköğretim Okulu’nda ve Kadirli Gülten-Ali Ziyan Anadolu Lisesi’nde
tamamladı. 2004 yılında kazandığı Atatürk Üniversitesi Kazım Karabekir Eğitim Fakültesi
Matematik Anabilim Dalı’nı 2009 yılında başarıyla bitirdi. Lisansla Birleştirilmiş Tezsiz
yüksek lisans öğreniminin ardından 2009 yılında tezli yüksek lisans öğrenimine Ahi Evran
Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalında başladı. Tezli yüksek
lisans eğitimi sırasında matematik öğretmeni olarak Gaziantep’in Nizip ilçesi Hüseyin
Yalçın Çapan Lisesi’ne atandı. Daha sonra Kırşehir Ticaret Meslek Lisesi’nde göreve
başladı. Halen bu görevine devam etmektedir.
73