Örnek. 6 defa Regula Falsi Yöntemini kullanarak f x 2 x 2 x 5 0 denkleminin yaklaşık
kökünü bulunuz.
Çözüm:
Denklemin kök aralığını bulmak için 2 yol kullanılır.
1. Garfiksel Metod
2. Analitik Metod
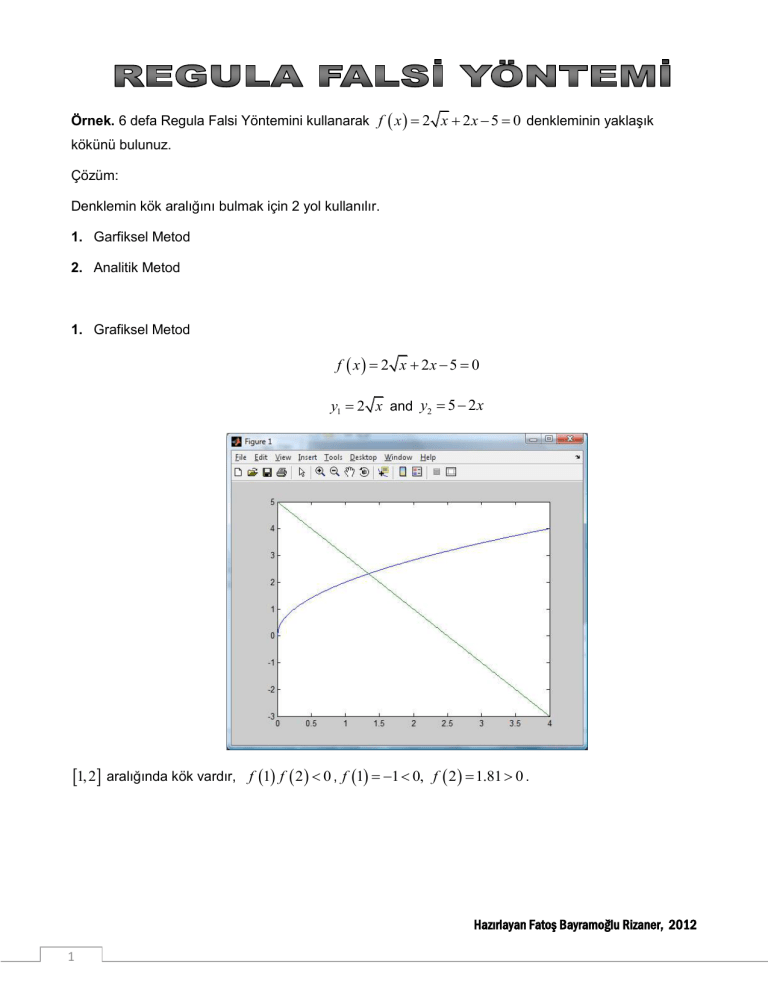
1. Grafiksel Metod
f x 2 x 2x 5 0
y1 2 x and y2 5 2 x
1, 2 aralığında kök vardır,
f 1 f 2 0 , f 1 1 0, f 2 1.81 0 .
Hazırlayan Fatoş Bayramoğlu Rizaner, 2012
1
2. Analitik Metod
f x 2 x 2x 5 0 f x
1
1
2 0, x .
4
x
x
0
1
8
1
4
1
3
2
2
Sign of f x
-
-
-
-
+
+
1, 2 veya
3
1, 2 aralıklarında kök vardır.
Regula Falsi Yöntemiyle f x 2 x 2 x 5 0 fonksiyonunun 1, 2 aralığında yaklaşık kökünü
bulalım. Regula Falsi Yöntemi,
xi b f b
ba
, i 1, 2,3, 4,...
f b f a
1. a 1, b 2, f 1 1, f 2 1.828427
2 1
x1 2 1.828427
1.353553
1.828427 1
x
1
1.353553
2
Sign of f x
-
+
+
2 a 1, b 1.353553, f 1 1, f 1.353553 0.033952
x2 1.353553 0.033952
1.353553 1
1.341943
0.033952 1
x
Sign of f x
1 1.341943 1.353553
-
+
+
Hazırlayan Fatoş Bayramoğlu Rizaner, 2012
2
3. a 1, b 1.341943, f 1 1, f 1.341943 0.000731
x3 1.341943 0.000731
1.341943 1
1.341693
0.000731 1
x
1
Sign of f x
-
1.341693 1.341943
+
+
4. a 1, b 1.341693, f 1 1, f 1.341943 0.000015
1.341693 1
x4 1.341693 0.000015
1.3416879
0.000015 1
x
1
Sign of f x
-
1.3416879 1.341693
+
+
5. a 1, b 1.3416879, f 1 1, f 1.3416879 0.00000845
1.3416879 1
x5 1.3416879 0.000000845
0.000000845 1
1.3416876
x
1
1.3416876
1.3416879
Sign of f x
-
-
+
6. a 1.3416876, b 1.3416879, f 1.3416876 0.0000000138, f 1.3416879 0.00000845
x6 1.3416879 1.38 108
1.341687905
1.3416879 1.3416876
8.45 107 1.38 108
x
Sign of
f x
1.3416876 1.341687905 1.3416879
-
+
+
Hazırlayan Fatoş Bayramoğlu Rizaner, 2012
3
Regula Falsi Yönteminin f x 2 x 2 x 5 0 fonksiyonu için 6 defa uygulanıp yaklaşık kök bulma
tablosu aşağıda gösterilmiştir.
Regula Falsi Yöntemi
xk b f b
ba
f b f a
f xk
xk 1 xk
1.353553
0.033952
1
1.353553
1.341943
0.000731
0.353553
1
1.341943
1.341693
0.000015
0.341943
3
1
1.341693
1.3416879
0.000000845
0.341693
4
1
1.3416879
1.3416876
-0.0000000138
0.3416879
1.341687905
0.0000008595
0.0000003
n
xk
xk 1
0
1
2
1
1
2
5
1.3416876 1.3416879
Hazırlayan Fatoş Bayramoğlu Rizaner, 2012
4
