BÖLÜM 3
DOĞRULTUCULAR
Amaç: Yarım dalga ve tam dalga doğrultucuların incelenmesi.
BİLGİ
3.1 Yarım Dalga Doğrultucu: Bir yöndeki akıma çok küçük bir direnç, zıt yöndekine ise
büyük bir direnç gösteren elektriksel düzen doğrultucu olarak adlandırılabilir. Pratikte
doğrultucu alternatif, yani şebeke geriliminden (AC) doğru gerilim (DC) elde edilmesi
amacıyla kullanılır. Yarı iletken bir diyotla gerçekleştirilebilen ve yarım dalga doğrultucu
(“half-wave rectifier”) olarak isimlendirilen en basit doğrultucu Şekil 3.1’deki gibi
gerçekleştirilebilir.
Doğrultucu girişine uygulanan, başka bir
deyişle
transformatörün
sekonder
çıkışındaki Vi Vm sin t gerilimi ile R L
yük direncinden geçen i akımı, t
ise,
0 için i I m sin d
2 için i 0
(3.1-a)
(3.1-b)
dir. Vi ve i’nin değişimleri Şekil 3.2’deki gibidir.
Devrede kullanılan diyotun ideal diyot olarak kabul edilmesiyle, R L yük direncindeki akımın
I m genliği
Im
Vm
R f RL
şeklindedir. Bu bağıntıdaki R f ideal diyotun geçirme yönündeki sabit direncidir.
(3.2)
Devrenin i akımının ortalama değeri, (1.2) ile
I dc
1
2
2
I m sin d
0
Im
(3.3)
olarak verilir. Akımın efektif veya rms değeri ise, (1.1) bağıntısına göre
I rm s
1 2
I m sin 2 d
2 0
1/ 2
Im
2
(3.4)
şeklindedir.
Doğrultucu çıkışında elde edilen gerilimin yüke bağlı olarak değişeceği aşikardır. Yük
olmadığı durumda Vdc çıkış geriliminin, teorik olarak
Vdc Vm / 0,318Vm
(3.5)
olacağı kolayca anlaşılabilir. Gerçekte çıkış gerilimi, transformatörün sekonder çıkış
geriliminden diyot üzerinde düşen miktar (örneğin Si diyotta VD 0,7V ) kadar daha azdır.
3.2 Tam Dalga Doğrultucu: Bir tür tam
dalga doğrultucu devresi Şekil 3.3’deki
gibi gerçekleştirilebilir. Böyle bir devre
tam-dalga köprü doğrultucu olarak anılır.
Köprü düzeninde bağlanmış dört diyottan
ikisi, örneğin D2 ve D3 diyotları iletimde
ise diğer ikisinin kesimde olacağı kolayca
anlaşılabilir. Vi
geriliminin negatif
alternansında ise D1 ve D4 diyotları
iletimde, diğerleri kesimdedir.
Vi giriş gerilimine bağlı olarak R L yük direncinden geçen i akımının değişimi Şekil 3.4’deki
gibidir. Bu takdirde tam dalga doğrultucu için (3.3) ve (3.4) ifadelerinin benzerleri
I dc
2I m
(3.6)
Im
(3.7)
I rm s
2
şeklindedir. Dolayısıyla doğrultucu çıkışında yük olmadığı durumda elde dilebilecek Vdc
gerilimi teorik olarak
Vdc 2Vm / 0,637Vm
(3.8)
olmalıdır. Gerçekte ise bu gerilim giriş gerilimine göre 2VD kadar daha azdır.
3.3 Dalgacık Katsayısı: Bir doğrultucuda amaç alternatif gerilimden sabit bir doğru gerilim
elde etmektir. Ancak yukarıda değinilen diyotlu doğrultucularla bu amaç istenildiği gibi
gerçekleşmemekte ve çıkışta Şekil 3.2-b) ve Şekil 3.4-b)’dekiler gibi dalgalı bir gerilim elde
edilmektedir. Bunun nedeni çıkış geriliminin alternatif bileşenidir.
Doğrultucu çıkışındaki gerilimin dalgalanmasının ölçüsü
factor”) ile verilir. Bu katsayı
r
r
dalgacık katsayısı (“ripple
ac bileşenin rms değeri
dalganın ortalama değeri
şeklinde tanımlanır. Dolayısıyla
r
s I rm
s
Vrm
Vdc
I dc
(3.10)
s , gerilim ve akımın ac bileşenlerinin rms değerleri, Vdc ve
s ve I rm
dir: Bu bağıntıdaki Vrm
I dc ise ortalama değerlerdir.
Çıkış akımının ac bileşeninin i ani değeri, i giriş akımının ani değeri ise,
i i I dc
dir. Bu takdirde (3.4)’den
s
I rm
1
2
2
i I dc
2
0
olacak ve bu ifadenin çözümü de,
s I rm s2 I dc 2
I rm
d
şeklindedir. Dolayısıyla doğrultucu çıkışındaki dalganın r dalgacık katsayısı (3.10)’dan
I rms I dc
2
r
I dc
2
2
I
rms 1
I dc
(3.11)
dir. Elde edilen bu sonuç doğrultucunun cinsine, yani yarım dalga veya tam dalga olmasına
bağlı değildir. Yarım dalga doğrultucu için, (3.3) ve (3.4)’den
I rms I m / 2
1.57
I dc
Im / 2
olduğundan; yarım dalga doğrultucunun dalgacık katsayısı
r 1.57 2 1 1.21
(3.12)
dir. Benzer şekilde, tam dalga doğrultucu için de, (3.6) ve (3.7) bağıntılarıyla
I rm s I m / 2
1.11
I dc
2I m /
olduğundan,
r 1.112 1 0.482
(3.13)
dir. (3.12) ve (3.13) bağıntılarının sonuçlarından kolayca anlaşılacağı üzere tam dalga
doğrultucu çıkışındaki dalgalanma, yarım dalga doğrultucuya göre daha küçüktür. Bu ise tam
dalga doğrultucunun doğru gerilim elde etmek için daha elverişli olduğunu kanıtlar.
3.4 Filtre: Doğrultucu çıkışında elde
edilen DC gerilimin değişimlerini azaltmak
amacıyla filtre devrelerinden yararlanılır.
Çeşitli filtre devrelerine karşılık en basit
filtre bir kondansatörle gerçekleştirilebilir
(Şekil 3.5).
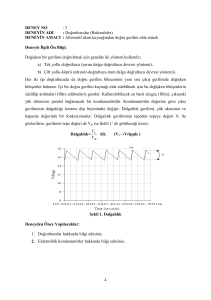
Yük olmadığı zaman filtre çıkışındaki Vc gerilimi, teorik olarak doğrultucudan elde edilen
gerilimin Vm tepe değerine eşit olup sabit kalacaktır. Yükün bulunması halinde ise Vc
kondansatör gerilimi Şekil 3.6’daki gibidir. Burada iki zaman aralığı vardır. T1 diyotun
iletimde olduğu süre, aynı zamanda kondansatörün şarj süresi olmasına karşılık, T2 diyotun
iletimde olmadığı ve kondansatörün yük üzerinden boşaldığı süredir.Kondansatörün çok az
boşalması halinde ortalama gerilim Vm değerine çok yakın olacaktır. Bu ise küçük bir yükle
sağlanır.
Kondansatör filtreli tam dalga doğrultucu çıkışındaki gerilimin, çıkış akımına bağlı
değişimleri hesaplamak için, Şekil 3.7’deki gibi çıkışı kırık düz çizgilerle düşünmek yararlı
olur.
Böyle bir yaklaşımla kondansatörün boşalması esnasındaki gerilim değişimi Vr ise Şekil 3.7a’dan Vdc ortalama değerinin,
Vdc Vm
Vr
2
(3.14)
olduğu kolayca anlaşılabilir. Ani dalgalanma veya dalgacık gerilimi ise çıkış geriliminin ani
değerinden Vdc ’nin çıkarılması ile elde edilebilir. Şekil 3.7-b’de bu gerilimin değişimi
görülmektedir. Dalgacık gerilimi üçgen dalga olduğuna göre efektif değeri (1.1) ’den kolayca
hesaplanabileceği gibi
s
Vrm
Vr
2 3
(3.15)
dür. Ancak T2 , diyotunun iletimde olmadığı ve kondansatörün deşarj süresini belirlediğine
göre, I dc sabit deşarj akımı ile kondansatördeki yük azalımı I dc T2 olacaktır. O halde
Vr
I dc T2
C
(3.16)
olmalıdır. Diğer taraftan iyi bir filtreleme için T1 süresinin mümkün olduğu kadar kısa, buna
karşılık T2 süresinin büyük olmalarının gerektiği kolayca anlaşılabilir. Bu takdirde T ve f
sırasıyla periyot ve frekans ise
T2
T
1
2 2f
Vr
I dc
2f C
olacaktır. Dolayısıyla
(3.17)
dir. Kondansatör filtreli tam dalga doğrultucunun r dalgacık katsayısı ise (3.10), (3.15) ve
(3.17) bağıntıları yardımıyla
r
s
Vrm
I dc
1
Vdc
4 3 f CVdc 4 3 f CRL
(3.18)
dir. Çıkış geriliminin I dc çıkış akımına bağlı değişimi de, (3.14) ve (3.17) bağıntılarından
Vdc Vm
I dc
4f C
(3.19)
şeklinde bulunur. Bu son bağıntılardan kolayca anlaşılacağı üzere dalgalanma ya da başka bir
deyişle dalgacık katsayısı yük direnci ve filtre kondansatörünün kapasitesi ile ters orantılı
olarak değişmektedir. Dalgalanmayı azaltmak için büyük kapasitelerin ( F mertebesinde)
kullanımı daha uygundur. Filtre devrelerine genellikle elektrolit kondansatörler kullanılır.
Aynı yaklaşımla kondansatör filtreli yarım dalga doğrultucu için r dalgacık katsayısı ile Vdc
çıkış geriliminin I dc yük akımına bağlı değişimini veren bağıntılar kolayca elde dilebilir. Tam
dalga doğrultucu için yukarıda verilen bağıntıların bir çoğu kondansatör filtreli yarım dalga
doğrultucu için de geçerlidir. Yegane fark T2 T / 2 olmayıp T2 T ’dir. Bu takdirde yarım
dalga doğrultucu için (3.17), (3.18) ve (3.19) bağıntıları
Vr
r
Vdc
I dc
fC
1
2 3 f CRL
I
Vm dc
2f C
( 3.17 )
( 3.18 )
( 3.19 )
şeklindedir. Bu son iki bağıntıdan da anlaşılacağı üzere yarım dalga doğrultucuda dalgacık
katsayısı ve yük direnci nedeniyle çıkış gerilimindeki azalma tam dalga doğrultucuya göre iki
misli daha büyüktür.
Diğer taraftan (3.19) bağıntısıyla
V
I dc
I dc
Vm Vdc veya m 1
Vdc
4 fCVdc
4 fC
ve (3.18) ifadesinden de
I dc 4 3 f CVdc r
olduğundan
4 3 f CVdc r
Vm
1
1 3 r
Vdc
4 f CVdc
veya
Vm 1 3 r Vdc
(3.20)
dir. Bu bağıntı doğrultucu çıkış geriliminin dalgacık katsayısı ile yük direncine bağımlılığının
yaklaşık ifadesidir.
Ancak bu son bağıntının kondansatör filtreli yarım dalga doğrultucu için de geçerli olduğu
(3. 19 ) ve (3. 18 ) ifadelerini kullanarak benzer şekilde kanıtlanabileceği kolayca anlaşılabilir.
DENEY
A)Yarım Dalga Doğrultucu Devresi:
1)Digiac
3000-2.1
Semiconductors-1
modülünün 2 nolu düzeni yardımıyla Şekil
3.8’deki devre gerçekleştirilir.
2)Devreye SG yardımıyla şehir şebekesininkine yakın bir frekansta ( 50Hz ) sinüs
gerilimi uygulanır. AC voltmetre olarak
kullanılan DM ile sinüs geriliminin rms
değeri 5V olacak şekilde ile genliği
ayarlanır.
3)Osiloskop yardımıyla SG çıkışındaki VSG ve 10K’lık
gerilimleri p-p ölçülerek, Tablo 3.1’e geçirilir.
R3 direnci
ucundaki VR 3
4)Bu değerlerden diyot uçları arasındaki VD3 gerilim düşmesi hesaplanarak; Tablo 3.1’e
geçirilir.
5)Osiloskopta görüntülenen giriş ve çıkış gerilim şekilleri çizilir. Bu eğride diyot
üzerinde düşen gerilim belirtilir.
6)DC voltmetre olarak kullanılan DM ile R3 direncinde düşen VR 3 gerilimi ölçülür. Bu
değer ayarlanan sinüs gerilim değeri ile kıyaslanır; sonuçlar Tablo 3.2’ye geçirilir.
Tablo 3.1
VSG V
VR 3 V
p p
p p
VD 3 V
p p
Tablo 3.2
VSG V
VR3 V
5
B) Kondansatör Filtresinin Etkisi:
1)Yük direncinin bulunmadığı Şekil 3.8’deki devreye kondansatör eklenerek Şekil 3.9’daki
devre gerçekleştirilir.
2)Devreye SG ile yukarıdaki gibi bir frekansta sinüs gerilimi uygulanır. DM yardımıyla sinüs
geriliminin rms değeri 5V olacak şekilde genliği ayarlanır.
3)Kondansatör uçları arasındaki VC 1
gerilimi DC voltmetre olarak kullanılan
DM ile ölçülür; sonuç Tablo 3.3’e geçirilir.
Bu ölçüm Tablo 3.2’deki VR 3 gerilimi ile
karşılaştırılır.
Tablo 3.3
VSG V
VC1 V
5
4)Şekil 3.9’daki devre değiştirilerek Şekil
3.10’daki devre oluşturulur. SG’nin çıkış
gerilimi, yukarıdaki gibi yine 5V’a
ayarlanır.
5)Osiloskopla gözlenen kondansatör uçları
arasındaki gerilim çizilir.
6)Çizilen bu eğriden kondansatör uçları
arasındaki gerilimin Vm maksimum değeri
belirlenir, sonuç Tablo 3.4’e işlenir.
7)Bu eğriden Vr tepeden tepeye dalgalanma gerilimi yaklaşık belirlenir. Bu değerden
Vort Vdc ortalama gerilimi (3.14) bağıntısı yardımıyla hesaplanır. Sonuçlar Tablo 3.4’e
geçirilir.
8)DC voltmetre olarak kullanılan DM ile yük direncindeki VR 3 gerilim düşmesi ölçülür, sonuç
Tablo 3.4’e işlenir.
9)Bu değerlerden (3.20) bağıntısı yardımıyla r dalgacık katsayısı belirlenerek Tablo 3.4’e
yazılır.
Tablo 3.4
Vm V
Vr V
p p
Vort V
VR3 V
r
10)Ölçülen VR gerilimi ile 10K yük direncinden geçen I ort I dc ortalama akımı Ohm kanunu
yardımıyla hesaplanır. SG ile devreye uygulanan f frekansı bilindiğine göre ( 3.17 )
bağıntısından Vr dalgalanma gerilimi, ( 3.18 )’den r dalgacık katsayıcı ve ( 3.19 )’dan
Vort Vdc gerilimi hesaplanır. Sonuçlar Tablo 3.5’e geçirilir.
11)Bu tablodaki değerler Tablo 3.4’dekilerle karşılaştırılır.
Tablo 3.5
f Hz
I dc mA
Vr V
Vort V
r
C) Negatif Güç Kaynağı:
1)Yarım dalga doğrultucu negatif gerilim
kaynağı Şekil 3.11’deki devre ile
gerçekleştirilir.
2)Devreye SG ile yukarıdaki gibi bir
frekansta sinüs gerilimi uygulanır ve
genliği DM ile yukarıdaki gibi 5V’a
ayarlanır.
3)Osiloskopta görüntülenen giriş ve çıkış
gerilimleri çizilir.
4)DC voltmetre olarak kullanılan DM ile R3 yük direnci üzerindeki VR 3 gerilim düşmesi
ölçülerek Tablo 3.6’ya geçirilir. Sonuç Tablo 3.2’deki değerle karşılaştırılır.
Tablo 3.6
VR3 V
D) Köprü Tipi Tam Dalga Doğrultucu:
1)Digiac
3000-2.1
Semiconductors-1
modülünün
3
nolu
düzeninden
yararlanılarak Şekil 3.12 ‘deki devre
gerçekleştirilir. Devrenin topraklanması
için 2 nolu düzenden faydalanılır.
2)Osiloskopla 10K’lık R4 yük direnci
üzerindeki
gerilim
düşmesi,
yani
doğrultucu
çıkışındaki
gerilim,
görüntülenir.
3)Bu devre çıkışını diyot gerilimi ile
karşılaştırmak için, Digiac 3000-2.1
Semiconductors-1
modülünün 2 nolu
düzeninden yararlanılarak Şekil 3.13’deki devre de gerçekleştirilir. İki devre için müşterek
topraklama yapılır.
4)SG’nin frekansı ayarlanarak osiloskopta gözlenen şekillerin ekranda mümkün olduğu kadar
sabit kalmaları sağlanır.
5)Osiloskopta görüntülenen tam dalga doğrultucu ile diyot çıkış gerilimleri çizilir.
6)Kondansatör
filtresinin
etkisinin
gözlenmesi için devreye 10 F ’lık C1
kondansatörü eklenir. Bunun için Şekil
3.12 ve Şekil 3.13’deki devreler beraberce
Şekil 3.14’deki gibi gerçekleştirilir.
7)C1 kondansatörü devreye bağlanmadan,
SG’nin frekansı ayarlanarak osiloskopta
gözlenen şekillerin mümkün olduğu kadar
sabit kalmaları sağlanır.
8)C1 kondansatörü şekilde gösterildiği gibi
devreye bağlanır. Osiloskobun CH1 ’inde
görüntülenen şekil çizilir.
9)Kondansatörün (+) ucu ile diyodun katot
ucu birleştirilir. Osiloskobun CH2 ’si ile
gözlenen kondansatör gerilimi aynı eğri
üzerine çizilir.
SORULAR
1)Yük direncine uygulanan sinüs geriliminin maksimum değeri 12V ve dalgacık geriliminin
tepeden tepeye 2V ise Vout çıkış gerilimi ne kadardır?
2) Yarım dalga doğrultucu devresine uygulanan sinüs geriliminin genliği 20V ise Vrms çıkış
gerilimi nedir?
3)Tam dalga doğrultucu devresi nasıl gerçekleştirilir?
4)Tam dalga doğrultucunun yarım dalga doğrultucuya göre en önemli özelliği nedir?