1
By Gökhan Bilhan
Calculus 2
(Week 1)-Denite Integrals
Example:The number of liters of blood your heart pumps in a xed time interval is called your
cardiac output.
For a person at rest, the rate might be 5 or 6 liters per minute.
During heavy exercise, the rate might be as high as 30 liters per minute.
How can a physician measure a patient's cardiac output without interrupting the ow of blood?
One technique is to inject a dye into a main vein near the heart.
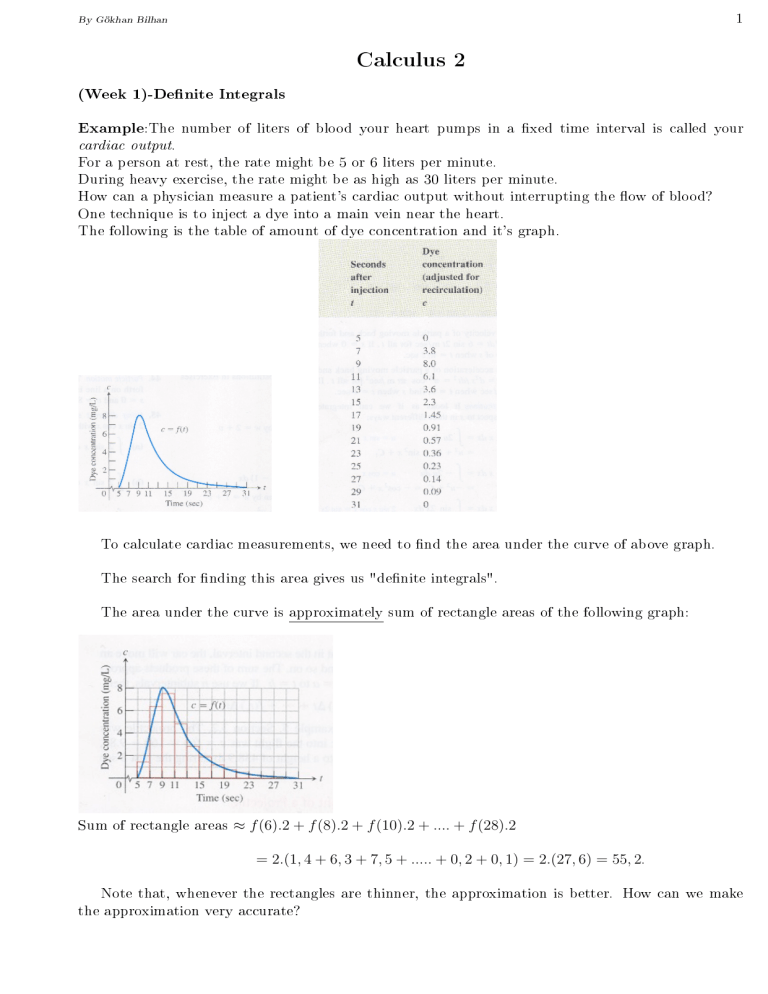
The following is the table of amount of dye concentration and it's graph.
To calculate cardiac measurements, we need to nd the area under the curve of above graph.
The search for nding this area gives us "denite integrals".
The area under the curve is approximately sum of rectangle areas of the following graph:
Sum of rectangle areas ≈ f (6).2 + f (8).2 + f (10).2 + .... + f (28).2
= 2.(1, 4 + 6, 3 + 7, 5 + ..... + 0, 2 + 0, 1) = 2.(27, 6) = 55, 2.
Note that, whenever the rectangles are thinner, the approximation is better. How can we make
the approximation very accurate?
By Gökhan Bilhan
Riemann Sums
Here is a typical continuous function:
We choose n − 1 points {x1 , x2 , ....., xn−1 } between a and b satisfying
2
By Gökhan Bilhan
3
So the sum of areas of rectangles is
The sum SP is called a Riemann Sum for f on the interval [a, b].
There are many such sums depending on the partition P we choose and the choices of the points
ck in the subintervals.
Which choice is better?
4
By Gökhan Bilhan
Denition:(The Denite Integral as a Limit of Riemann Sums) Let
f be a function dened on a
closed interval [a, b]. For any partition P of [a, b], let the numbers ck be choosen arbitrarily in the
subintervals [xk−1 , xk ].
If there exists a number I such that
lim||P ||→0
n
∑
(||P || is the longest subinterval length).
f (ck )△xk = I
i=1
No matter how P and the c′k s are choosen, then f is integrable on [a, b] and I is the denite integral
of f over [a, b].
The problem is calculation of integrals are not easy.
Theorem All continuous functions are integrable. That is, if a function f is continuous on an interval
[a, b], then it's denite integral over [a, b] exists.
We represent
lim||P ||→0
n
∑
i=1
∫
f (ck )△xk = I =
b
f (x)dx
a
5
By Gökhan Bilhan
Denition:(Antiderivative of a Function) A function F is an antiderivative of a function f , if
F ′ (x) = f (x)
Example: (1) Let's nd three antiderivatives of 2x.
(2) How many anti-derivatives of 2x exists and how are they related?
Theorem: If F and G are dierentiable functions and F ′ (x) = G′ (x) for all x, then F (x) = G(x) + k
for some constant k.
That is,..
Theorem(Fundamental Theorem of Calculus) If f is continuous over the interval [a, b], then
∫
b
f (x)dx = F (b) − F (a)
where F (x) is antiderivative of f (x).
a
Now, let's do some work about antiderivatives.
We represent the antiderivative of a function f (x) by F (x) =
∫
f (x)dx.
Antiderivative of a function is called the indenite integral of the function.
That is,
∫
f (x)dx = F (x) + C ,
∫
Note that the symbol
if F ′ (x) = f (x).
is called the integral sign.
The function f (x) is called the integrand.
The symbol dx indicates that the anti-dierentiation is performed with respect to the variable x.
The arbitrary constant C is called the constant of integration.
By Gökhan Bilhan
Example:
∫
x2 dx
∫
s2 ds
∫
t2 dt
Basic Properties.
1-)
2-)
3-)
4-)
5-)
6-)
7-)
∫
xn+1
x dx =
+ C , where n ̸= −1.
n+1
n
∫
∫
ex dx = ex + C .
1
dx = ln|x| + C , where x ̸= 0.
x
∫
∫
∫
(f (x) ± g(x))dx = f (x)dx ± g(x)dx.
∫
∫
For k, a constant, kf (x)dx = k f (x)dx.
∫
sinxdx = −cosx + C .
∫
cosxdx = sinx + C .
Examples
1-)
2-)
3-)
4-)
∫
5dx
∫
9ex dx
∫
5t7 dt
∫
(4x3 + 2x − 1)dx
6
7
By Gökhan Bilhan
5-)
6-)
7-)
8-)
∫
∫
∫
∫
3
(2ex + )dx
x
√
3
5 u2 du
x3 − 3
dx
x2
√
2
(4sinx + √
x)dx
−
6
3
x
Remark. Note that in general,
9-)
∫
x(x2 + 2)dx
∫
∫
f (x)g(x)dx ̸=
∫
f (x)dx
g(x)dx
8
By Gökhan Bilhan
1.
2.
3.
4.
5.
Exercises
∫
exdx
∫
(10x4 −
∫
12 + 5z − 3z 3
dz
z4
∫
(
∫
8
− 2)dx
x5
2
5
−
)dx
3x2 4x3
1 + t2
dt
t
∫ √
4
6. ( 3 x2 − 3 )dx
x
By Gökhan Bilhan
7.
8.
9.
10.
11.
∫
∫
√
2
(3 x + √ )dx
x
ex − 3x
(
)dx
4
∫
(
x5 − 2x
)dx
x4
∫
(1 + x)(1 − x)dx
∫
(2ex + cosx)dx
9
10
By Gökhan Bilhan
Integration By Substitution
Example: Let's evaluate the integral I =
Example: Let's evaluate the integral I =
Example: Let's evaluate the integral I =
∫
(x2 + 2x + 5)(2x + 2)dx
∫
2
e(t ) 2tdt
∫
1
2xdx
4 + x2
11
By Gökhan Bilhan
Example: Let's evaluate the integral I =
Example:Let's evaluate the integral I =
Example:Let's evaluate the integral I =
Example:Let's evaluate the integral
∫
∫
∫
1
dx
4x + 7
√
4x2 x3 + 5dx
x
√
dx
x+2
∫
cosπtdt
By Gökhan Bilhan
Exercises
1.
2.
3.
∫
(3x + 5)2 3dx
∫
(x6 + 1)4 (6x5 )dx
∫
x
dx
1 + x2
∫ √
4.
1 + x4 (4x3 )dx
5.
∫
(x + 3)10 dx
12
By Gökhan Bilhan
6.
7.
8.
9.
10.
∫
3
dt
2−t
∫
√
x
dx
x+5
∫
x(x + 6)8 dx
∫
∫
e−x (1 − e−x )4 dx
(lnx)3
dx
x
13
By Gökhan Bilhan
(Week 1)-Area Problem and Indenite Integral
Exercises
1.
2.
3.
4.
5.
∫
∫
√
1
( x + √ )dx
x
√
√
t t+ t
(
)dt
t2
∫
(−2cost)dt
∫
√
2x2 + x2 x − 1
(
)dx
x2
∫
(1 − t)(2 + t2 )dt
14
By Gökhan Bilhan
6.
7.
8.
9.
10.
∫
∫
√
2x + 1dx
lnx
dx
x
∫
esinx cosxdx
∫
∫
√
sin x
√ dx
x
ex + 1
dx
ex
15
16
By Gökhan Bilhan
11. I =
∫
√
x x + 1dx
12. For a real number k, evaluate the integrals I =
∫
sinkxdx and I =
∫
coskxdx.
