LYS1 / 7.DENEME
MATEMATİK TESTİ ÇÖZÜMLERİ
1.
a
-
b
c
5
a = b.c + 5
a
-
c
5.
b
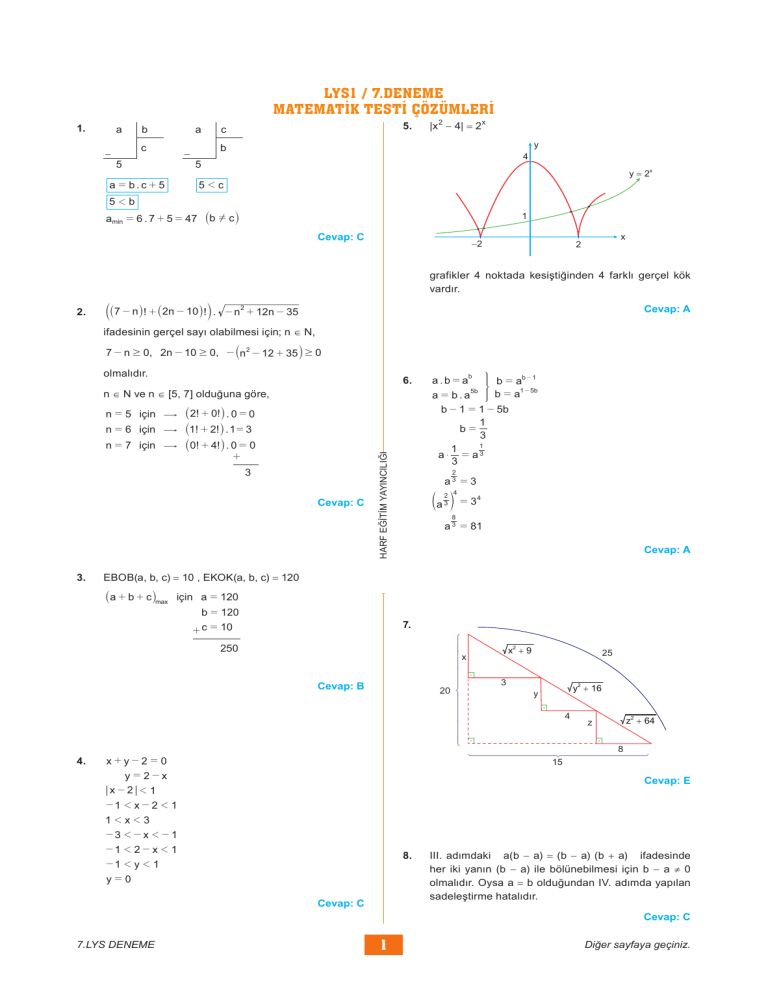
|x 2 - 4| = 2x
y
4
5
y = 2x
5<c
5<b
Y cj
amin = 6 . 7 + 5 = 47 `b =
1
Cevap: C
−2
2.
b`7 - n j ! + `2n - 10 j ! l . - n 2 + 12n - 35
ifadesinin gerçel sayı olabilmesi için; n ∈ N,
7 - n $ 0, 2n - 10 $ 0, - `n 2 - 12 + 35 j $ 0
olmalıdır.
n ∈ N ve n ∈ [5, 7] olduğuna göre,
n = 5 için $ `2! + 0! j . 0 = 0
6.
n = 7 için $ `0! + 4! j . 0 = 0
+
3
Cevap: C
EBOB(a, b, c) = 10 , EKOK(a, b, c) = 120
`a + b + c jmax için a = 120
HARF EĞİTİM YAYINCILIĞI
n = 6 için $ `1! + 2! j . 1 = 3
3.
grafikler 4 noktada kesiştiğinden 4 farklı gerçel kök
vardır.
b = 120
Cevap: A
b-1
a . b = ab
4 b = a1 - 5b
5b
=
b
a
a = b.a
b - 1 = 1 - 5b
1
b=
3
1
1
3
a$ = a
3
2
a3 = 3
ca 3 m = 34
2
8
a 3 = 81
Cevap: A
7.LYS DENEME
x2 + 9
x
Cevap: B
20
x+y-2 = 0
y = 2-x
x-2 < 1
-1 < x - 2 < 1
1<x<3
-3 < - x < - 1
-1 < 2 - x < 1
-1 < y < 1
y=0
250
4.
4
7.
+ c = 10
x
2
8.
Cevap: C
y2 + 16
y
4
z
z2 + 64
8
15
Cevap: E
III. adımdaki a(b - a) = (b - a) (b + a) ifadesinde
her iki yanın (b - a) ile bölünebilmesi için b - a ≠ 0
olmalıdır. Oysa a = b olduğundan IV. adımda yapılan
sadeleştirme hatalıdır.
1
3
25
Cevap: C
Diğer sayfaya geçiniz.
9.
` x 2 - 5x j - 2 ` x 2 - 5x j - 24
13. Veri grubunda iki tane 2 olduğundan, 5ʼin tepe değer
olması için en az üç tane 5 bulunması gerekir.
2
2
x - 5x = a olsun.
a 2 - 2a - 24 = `a - 6 j`a + 4 j
= ` x - 5x - 6 j` x - 5x + 4 j
2
2
= ` x - 6 j` x + 1 j` x - 4 j` x - 1 j
O halde, a - 2 = 5
ve
b+3=5
a=7
ve
b=2
a . b = 14
5
(x - 2) çarpan değildir.
-
Cevap: E
4
10. A = {1, 2, 3, 4} kümesinin; 24 = 16 tane alt kümesi vardır.
16 elemanlı kuvvet kümesinin en çok 2 elemanlı alt
kümeleri:
16
16
16
f p + f p + f p = 120 + 16 + 1 = 137
2
1
0
Cevap: A
i1 = i
i2 = - 1
i3 = - i
i4 = 1
14.
Cevap: YÜZOTUZYEDİ
11.
f p+f
f
n
r
n
n+1
p=f
p olduğundan;
r+1
r+1
32
32
32
32
p+f p+f p+ g +f p
0
2
4
32
644444474444448 644444474444448
644444474444448
31
31
31
31
31
31
31
f p+f p+f p+f p+f p+ g +f p+f p
0
1
2
3
4
30
31
= 231
HARF EĞİTİM YAYINCILIĞI
Cevap: B
_b
bb
bb
bb
b`b
bb
bb
b
a
olduğundan i2n biçimindeki ifadeler reel
sayıdır.
2 basamaklı çift sayılar:
10, 12, 14, g, 98
144444444424444444443
98 - 10
+ 1 = 45 tanedir.
2
Cevap: A
15. Bölünen ve bölen polinomları yer değiştirdiğinde kalanlar birbirinin ters işaretlisi olacağından;
ax - 12 = - `3x + b j
ax - 12 = - 3x - b
a =- 3
b = 12
a+b = 9
12.
Cevap: A
16.
P _ x i = ` x 2 - 2 j . B _ x i + `2x - 1 j
2
2
P _ x i = ` x 2 - 2 j . B _ x i + 2 ` x 2 - 2 j . B _ x i . `2x - 1 j + `2x - 1 j
14444444444444444444444444244444444444444444444444443 1444442444443
2
1
f p=1
1
kalan 0
f p+f p+f p = 7
kalanı bulmak için x 2 - 2 = 0
5
5
5
5
5
f p + f p + f p + f p + f p = 31
1
2
3
4
5
1 . 7 . 31 = 217
4x 2 - 4x + 1 $ 4 . 2 - 4x + 1
$ 8 - 4x + 1
$ 9 - 4x
3
1
3
2
7.LYS DENEME
2
3
3
Cevap: D
2
4x 2 - 4x + 1
x 2 = 2 olmalıdır.
Cevap: C
Diğer sayfaya geçiniz.
x 2 + `m + 1 j x + n 2 + 8 = 0
17.
denkleminin kökleri x1 = p x 2 = p + 1 olmalıdır.
D
Kökler farkı
= 1 olmalıdır.
a
y # 6x - x 2
21.
y $ x-6
y
`m + 1 j - 4n 2 - 32 = 1
2
0
y
6
x
2
m = - 18
veya
m - 2n + 1 = 1
veya
m - 2n + 1 = - 3
m + 2n + 1 = - 11
y
m =- 8
veya
O
m - 2n + 1 = 3
m + 2n + 1 = 11
m + 2n + 1 = 33
m = 16
Ç.K. = {-18, -8, 6, 16} sağlayan değerler D şıkkında
{-18, 16}
Cevap: D
x 2 - 2px + p - 1 = 0
x1 + x 2 = 2p
x + x = 2 ` x1 x 2 + 1 k
4 1 2
x1 $ x 2 = p - 1
x1 + x 2 = 2x1 x 2 + 2
18.
Cevap: A
x + 1 $ x - 3 `x - 2j
7
19.
`x - 6j
11
x
f(x)
Tanımsız
+
−
−
y
y = x2 − ax + b
y = x2 − cx + d
x1
−2
5
x
- 2 + x1 = a
x1 + 5 = c
- 2 . x1 = b
x1 . 5 = d
- 35
d
5
`c - a j $ = 7 $
=
b
-2
2
6
3
Cevap: E
22.
<0
−1
x
6
−6
m=6
HARF EĞİTİM YAYINCILIĞI
x
−6
`m - 2n + 1 j`m + 2n + 1 j = 33
m - 2n + 1 = - 1
m + 2n + 1 = - 33
6
0
`m + 1 j - _2n i = 33
2
+
Cevap: B
4 ve 5
2 tane
Cevap: B
23.
f _ x i tek ise f `- x j = - f _ x i
g _ x i çift ise g `- x j = g _ x i
a gof k`- x j = g b f `- x jl = g b- f _ x il = g b f _ x il = a gof k_ x i
çift
20.
x 2 + mx + n = 0,
x1 + x 2 = - m
x1 $ x 2 = n
I
m.n < 0
x
- ` 1 + x 2 k` x1 x 2 j < 0
0 < a < b ya da
` x1 + x 2 k` x1 x 2 j > 0
7.LYS DENEME
7
7
f `- x j = b - f _ x i l = - f _ x i
7
tek
II a < 0 < b ve a > b
a f . g k`- x j = f `- x j $ g `- x j = - f _ x i $ g _ x i = - a f . g k_ x i
tek
ne tek a f + g k`- x j = f `- x j + g `- x j = - f _ x i + g _ x i
ne çift
` fof j`- x j = f b f `- x jl = f b- f _ x il = - f b f _ x il = - ` fof j_ x i
tek
Cevap: E
3
Cevap: C
Diğer sayfaya geçiniz.
24.
y
y=x
y = f(x)
27.
y = f−1(x)
1
−1
x
`an j = f
2
3n - 3n + 8
p
n+1
n+1
3n - 6
3n 2 - 3n + 8
- 3n 2 + 3n
- 6n + 8
- - 6n - 6
14
`an j = f 3n - 6 +
y
y = f−1(x)
1
0
x
1
14
p
n+1
a1, a6, a13 tam sayıdır.
3 tane
Cevap: D
28. `an j aritmetik dizi,
a5 = 3
Cevap: A
y
y = f(x)
2
a1 + a15
p
2
= 15 $ f
a5 + a11
p
2
= 15 $ f
3 + 11
p
2
= 105
2
x
0
S15 = 15 $ f
y
y = f(−x)
x
0
y
x
0
HARF EĞİTİM YAYINCILIĞI
25.
29.
Cevap: D
a3 = b 45
a = b15
1
log a b = logdb15 n `b j2
1
= 2 $ logb b
15
1
=
30
−2
y = −f(−x)
y
30.
x
0
a11 = 11
−1
Cevap: D
3x = 2
ve
3x = 3
x = log3 2
x=1
log3 2 + 1 = log3 2 + log3 3
= log3 `2 $ 3 j
= log3 6
y = 1 − f(−x)
Cevap: B
x
26.
f(x) =
xʼten küçük en
büyük tam sayı
f `- 2, 3 j + f _1 i
f ` e j - f `r j
=
,
x∈Z
,
x ! Z
31.
`- 3 j + 1
7.LYS DENEME
2 - 1l a
-2
-1
=2
2 + 1 k + log 2 8
f
= logb
2 - 1l
= logb
2 - 1l a
=- 1 +
2-3
=
logb
Cevap: B
=5
3
1
2
1
p + log 2 8
2-1
3
2 - 1 k + log 2 2
-1
1
2
Cevap: C
Cevap: A
4
Diğer sayfaya geçiniz.
32.
1
1
+
=4
1 - cos x 1 + cos x
1444442444443 1444442444443
a1 + cos x k
36.
f_xi =
Tanımsız olduğu noktalar;
sin x = 0
x = 0, x = r
a1 - cos x k
1 + cos x + 1 - cos x
=4
1 - cos 2 x
2
=4
sin 2 x
1
sin 2 x =
2
-1
1
sin x =
sin x =
2
2
r , 3r
4
`0, r j 'de Ç. K. = *
4 4
cot x
sin x + cos x
cos x
=
sin x `sin x + cos x j
sin x + cos x = 0
sin x = - cos x
tan x = - 1
3r
x=
4
3 tane
Cevap: B
Cevap: E
y
37.
33.
26a = r
r
13a =
2
−7
cos 12a - cos 2a
=
sin 15a - sin a
sin `13a + 2a j - sin a
r
- a p - cos 2a
2
sin f
r
+ 2a p - sin a
2
sin a - cos 2a
=
cos 2a - sin a
=- 1
Cevap: D
a
b
c
34.
=
=
sin Ac sin Bc sin Cc
a+b
c
=
sin Ac + sin Bc sin Cc
12
c
=
W
W
6 $ sin C sin C
c=2
Çevre ` ABC j = a + b + c = 14 br
Z U
12
3
x
Z]
]]- 2 , f _ x i < 0
]]
g _ x i = [] 0 , f _ x i = 0
]]
] 2 , f_x i > 0
]
\
fonksiyonun kritik noktaları olan f(x) = 0 denkleminin
köklerinde limitsiz yani süreksiz olduğu görülür.
O halde, grafiğin Ox eksenini kestiği noktalar (kökler)
x = -7, -2, 1, 6
(-7) + (-2) + 1 + 6 = -2
38.
2
0 1
−1
y = f(x)
HARF EĞİTİM YAYINCILIĞI
=
cos f
6
−4 −2
cos `13a - a j - cos 2a
Cevap: B
lim a f + g k_ x i = lim a f + g k_ x i = a f + g k_2 i olmalıdır.
x " 2-
x " 2+
f `2 j + g `2 j = f `2+ j + g `2+ j = f _2 i + g _2 i
-
-
1 + g `2- j = - 1 + f `2+ j = 0 + g _2 i = A
ise g _2 i = A
Cevap: E
g `2- j = A - 1
35.
lim
x"3
3x + x
= lim
x " 3 1 - 2x
3x + x
= lim
x " 3 1 - 2x
= lim
x"3
3x 2 - 2x + 2 + 3 x3 + 1
g `2+ j = A + 1
koşulunu sağlayan grafik
1 - 2x
y
3
2
1
4 x
0
-2 x + 1
x
Cevap: D
7.LYS DENEME
4
−1
=- 2
2
5
Cevap: E
Diğer sayfaya geçiniz.
39.
y
x br
42.
a br
(x − a) br
y = f(x)
a
O
b
c
x
d
a
3
x = b ve x = d noktalarında fonksiyon süreksiz olduğu
için türevsizdir.
x = a ve x = c noktalarında grafik kırılma yaptığından
sağdan ve soldan türevleri eşit olmayacağından türevsizdir.
I. a 3 x x k ' = c x m ' =
40.
x−a
4
x−a
4
2
a
f p $ 3
2
3
x-a
p
+f
S1 + S 2 =
4
4
d `S1 + S 2 k
da
=
x - a -1
a 1
1
p$
=0
$ 2 $ $ $ 3 + 2 $f
4
4
3 3
4
a 3 1 x-a
p
= $f
4
18
2
4a 3
= x-a
9
a
a
3 =
3
= 3
x-a
4a 3
4
9
4
1
2 x
II. f _ x i = g _ x i - x $ g' _ x i
f' _ x i = g' _ x i - :1 $ g' _ x i + x.g" _ x iD
= - x . g" _ x i
2
'
III. f :sin _ x iD = f' `sin 2 x j $ 2 sin x cos x
'
2
IV. ;f ` x 2 jE = 2f ` x 2 j $ f' ` x 2 j $ 2x
V. ;x 2 $ f ` x 4 jE ' = 2x $ f ` x 4 j + x 2 $ f' ` x 4 j $ 4x3
HARF EĞİTİM YAYINCILIĞI
= f' `sin 2 x j . sin 2x
= 4x $ f ` x 2 j $ f' ` x 2 j
= 2x $ f ` x 4 j + 4x5 $ f' ` x 4 j
Cevap: B
y = x 2 - 5x - 6 = ` x - 6 j` x + 1 j
x = 6 ve x = - 1
f' _ x i = 2x - 5
43.
m1 = f' `6 j = 7, m 2 = f' `- 1 j = - 7
-7 - 7
- 14
m 2 - m1
7
=
=
=
tan a =
1 + m1 .m 2 1 + 7 `- 7 j - 48 24
Cevap: A
y
41.
S2
a
3
Cevap: D
1
2
a
3
S1
cos a =
25
7
24
25
α
24
−1
2
3
x
Cevap: A
y = f'(x)
6
y
x
f"(x)
−∞
−
+
2
3x + 5 = a
3.dx = da
−
−1
f'(x)
azalan artan
# f`3x + 5j.dx = A
44.
3
−1
azalan
0
3
23
x
#
11
23
#
Cevap: C
11
7.LYS DENEME
6
f `a j $
da 1
=
3
3
23
#
11
f `a j $ da = A
f `a j $ da = 3A
Cevap: B
Diğer sayfaya geçiniz.
#
45.
49.
4
x-x
$ dx
x
12
x=m
dx = 12m11 $ dm
y
4
#
12
12
m -m
3
m12
3
$ 12m11 $ dm =
3
12
# m m- m
= 12 $
4
# `m
10
11
$ 12m $ dm
- m19 j $ dm
0
eğrilerinin kesim noktaları
x2 + f
r
2
0
2
=-
2
#
-2
= - f `u j
x2
f 8 - x - p $ dx
2
Cevap: B
# sin x $ cos 2x $ dx
5
3
sin5x.cos32x fonksiyonu tek fonksiyon olduğuna göre,
f(x) çift fonksiyondur.
-r
r
r
3r
p
ff p - ff p = ff p - ff
2
2
2
2
r
r
= ff p - ff p
2
2
=0
JK 1
NO
KK
O
KK `2a + b j $ daOOO $ db =
KK
OO
0
0
L
P
1
# #
48.
0
1
#
=
1
Cevap: A
50. f(x) = x3 - 3x 2 + 5x - 1 fonksiyonunun simetri merkezi
dönüm noktasıdır.
2
f' _ x i = 3x - 6x + 5
f" _ x i = 6x - 6 = 0
x=1
f _1 i = 1 - 3 + 5 - 1 = 2 S.M `1, 2 j
Cevap: C
1
0
= - f `0 j + f _1 i
= 3+0
=3
2
f_x i =
# f'`uj . du
1
çember ile parabol arasındaki alanı
47.
cos x = u
- sin x . dx = du
HARF EĞİTİM YAYINCILIĞI
# sin x . f'`cos xj . dx
0
x
p =8
2
x =! 2
2
JK
1 N
OO
KK 2
O
`
j
KKK a + ab OOO $ db
0
L
P
g_x i =
mx + 2
fonksiyonunun simetri merkezi asimpnx - 4
totlarının kesim noktasıdır.
# :`1 + bj - 0D $ db
yatay asimptot
1
# `b + 1j $ db
düşey asimptot
4 m
S.M f , p
n n
4
=1
n
n=4
0
=
b2
+b
2
1
0
1
= f + 1p - 0
2
3
=
2
7.LYS DENEME
y = lim g _ x i =
x "!3
y=
0
=
x
−3
x 2 + y 2 = 8 ise y = 8 - x 2
2
x
2
2
y=
ve
x +y = 8
2
1
2
Cevap: C
46.
y = f(x)
3
Cevap: B
7
ve
m
n
m
n
nx - 4 = 0
4
x=
n
b_b
m
bb
=2
`b m.n = 32
n
b
m = 2n = 8 bb
a
Cevap: OTUZİKİ
Diğer sayfaya geçiniz.
54.
4
$ r $ 33 = 36r br3
3
V2 = Vprizma = 10 $ 5 $ 3 = 150 br3
51.
V1 = Vküre =
2
V3 = Vsilindir = r $ 3 $ 10 = 90r br
V3 > V2 > V1
A
α
a
3
3k
B
Cevap: E
a
β
D
3k
E
a
120° a
α
C
&
&
ABF ve ECD üçgenlerinde sinüs teoremi yazılırsa;
a
3k
=
sin b sin a
3
= 3
(
2. sin b
a
3k
=
sin 120c sin a
1
sin b =
2
b = 150c
52.
D
16
C
7
24
H
7
E
32
HARF EĞİTİM YAYINCILIĞI
25
A
Cevap: A
B
16 + 32
p $ DA = 336 br 2
A ` ABCD j = f
2
DA = 14 br
&
AHE üçgeninde `7 - 24 - 25 j üçgeninden
AE = 25 br dir.
Cevap: C
55.
D
F
C
5
4
L
K
h
E
P
A
B
&
DEC ikizkenar üçgen
FK + FL = hc = DP
DP = 9 br
DE = EC olduğundan;
53.
A
x
F
D
Cevap: A
56.
21
A
84
2α
B
4k
E
3k
C
ADEF deltoit olup [AE] açıortaydır.
İç açıortay teoreminden;
42°
B
x
21
=
4k 3k
x = 28 br
7.LYS DENEME
E
F
2β
α
D
18°
C
a + b = 48
- a - b = 18
a = 33c
Cevap: A
8
Cevap: D
Diğer sayfaya geçiniz.
57.
A
α
2α
2α
E
θ γ
α
2θ
60.
d
β
F
C
11
C
10
F
10
B
A
K
D
D
α
169 − x2
x
α
2γ
β
E
2β
Q=c
&
&
ABD + ADF
AD
20
=
10
AD
AD = 10 2 br
13
B
` x + 11 j + a 169 - x k = 20 2
2
2
2
2
x + 22x + 121 + 169 - x = 400
22x = 110
x = 5 br
Cevap: C
Cevap: C
61.
A
2a
58.
2 10
D
C
a
2a
2 10
E
4
45°
45°
2
2
4
45°
45°
β
A α
2
2
F
HARF EĞİTİM YAYINCILIĞI
4 2
α
4
B
2
E
3a
D
sinx
cosx
B
ABC üçgeninde |BF| = 3a olup, BDE üçgeninde kenarortay teoreminden;
2 . `3a j +
2
`2a j
2
2
= sin 2 x + cos 2 x
20a 2 = 1
1
a=
2 5
5 . AC = 5 . 6a = 5 $
Cevap: D
6
= 3 br
2 5
Cevap: C
Şekil açılırsa;
62.
A
59.
6
E
2
D
4
α
B
a
C
Çevre ` ABCD j = 8 10 br
F
2α α
α
4
Şekil IV
H
4
C
&
ABC ikizkenar üçgen olduğundan, BH = CE
AE = AH
BE = HC
BDC üçgeni ikizkenar üçgen olduğundan |HC| = 4 brʼ dir.
7.LYS DENEME
Cevap: B
9
Cevap: C
Diğer sayfaya geçiniz.
63.
67.
d1 = x - 2y + 4 = 0
d 2 = 2x + my + 8 = 0
1 -2
Y
I.m = 4 için
olduğundan d1 // d2 değildir.
=
2
4
E
D
-2,
1
II.m = 1 için m1 = , m 2 =
m1 $ m 2 = - 1 olur.
2
1
d1 ⊥ d2ʼdir.
III.m = 2 için
C 2
3
5 2
L
4
x - 2y + 4 = 0
+ 2x + 2y + 8 = 0
3
5 2
A
15° 15°
20
Kosinüs Teoreminden;
13 = 29 + 50 - 2 . 5 2 . 29 . cos a
- 66
33
= cos a =
- 2 . 5 2 . 29
5 2 . 29
2S
D
2k
EB $ ET = EB $ ET $ cos a
33
= 5 2 $ 29 $
5 2 $ 29
= 33
C
1
$ 10 $ 20 $ sin 30c
2
1
= 100 $
2
= 50 br 2
100
2
Alan ` ADC j =
br
3
Alan ` ABC j =
Cevap: D
65.
Şekilde sadece 6 . 4 = 24 kare
alanı açıktadır.
Diğer yapılarda açıkta kalan
kare yüzey sayısının daha fazla olduğu görülür.
HARF EĞİTİM YAYINCILIĞI
Cevap: A
68.
Cevap: C
D
36° 30°
66.
A'
E
D'
D
13
C
5
5
α
ZEMİN A
12
B
10
B'"
β 5α
C'
12
β
13
12
A'"
36°
5
D'"
A
90c
90c
+ 2r $ 13 $
360c
360c
13r
= 6r +
2
25r
=
br
2
2 $ r $ 12 $
7.LYS DENEME
C
5 3
7
13
B
10
K
29
Cevap: E
k
13
T
B
3
B
x =- 4
4 `- 4, 0 j
y=0
S
2
4
E
3x + 12 = 0
64.
T
41
5
A
F
29
60°
12°
F
5
B
|AD| = |EC| = 10 br
Cevap: A
Cevap: D
10
Diğer sayfaya geçiniz.
A
69.
A
6 3
12
60°
30°
4
6
60°
E
2
60° 60°
30°
3
D
B
m
B
m
10 S
S
3
H
3
9D
E
n
9
C
E
n
C
A
A
3
30°
D
10
30°
B
S m
=
9
n
A
72.
D
S
10
C
B
|AD| = 12 br
Cevap: D
m
E
10
10
m
= m
n
SB+ 9
10
S
=
9 S+9
S `S + 9 j = 90
S
9D
n
9
C
n
C
E
2
S = 6 br
&
2
Alan` ABC j = 25 br
70.
Cevap: C
A S
S
S
S
C
E
Alan _DEF i
Alan ` ABC j
S
B
S
S
D
HARF EĞİTİM YAYINCILIĞI
F
=7
Cevap: B
A
73.
D
71.
B
A
6
H
F
6
4 P
2α
2β
α y
x z β
β
α
E
C
D
6
α
α
B
C
&
ADH dik üçgeninde hipotenüs dik kenarlardan daha
büyük olacağından;
|AD| > 6
|AD|min = 7
7.LYS DENEME
&
&
BDP + CEP
4 y
=
x z
Cevap: D
11
ve
,
& &
BEP + BFP
x y
=
6 z
4 x
=
x 6
2
x = 24
x = 2 6 br
Cevap: C
Diğer sayfaya geçiniz.
74.
77.
E
D
C
M(1, 2)
B
A
A
L
M
K
E, diklik merkezidir.
Cevap: E
3x − 4y = 0
1
r
3
H 3
B
noktanın doğruya uzaklığından;
3 .1 - 4 . 2
MH =
32 + 42
2
2
2
r = 3 + 1 = 10
r = 10 br
=
5
= 1 br
5
78.
Cevap: B
2a = 20 , a5, 4 3 k
a = 10
2
2
y
x
+
=1
100 b 2
x=5
25
48
4
+
=1
y = 4 3 100 b 2
48 3
=
2
4
b
2
b = 64
2
2
y
x
+
=1
100 64
y
7
7
D
17
B a
(17, 31)
31 − a
C
A
24
a
7 O 31 − a
B
25 D
C
x
17 + a = 31 − a
a=7
7
7
HARF EĞİTİM YAYINCILIĞI
75.
79.
CD
7
=
25
24
175
CD =
24
17
24
Cevap: A
2a = 12 ,
2b = 10
a=6
b=5
2
2
y
x
=1
36 25
Cevap: C
Cevap: A
80.
4
76.
x 2 + y 2 - 2x + 8y - 1 = 0
M `1, - 4 j olup A `3, - 6 j 'dan geçen çember,
r = MA =
3
2 + `- 2 j = 2 2
2
2
3
`x - 1j + ay + 4 k = 8
2
2
Yan yüzlerde 2ʼşer tane, tabanlarda 1ʼer tane olmak
üzere;
4 . 2 + 2 . 1 = 10
x 2 + y 2 - 2x + 8y + 9 = 0
Cevap: B
7.LYS DENEME
12
Cevap: ON
Diğer sayfaya geçiniz.
