6. BÖLÜM
MERCEKLER
ALIŞTIRMALAR 1
MERCEKLER
ÇÖZÜMLER
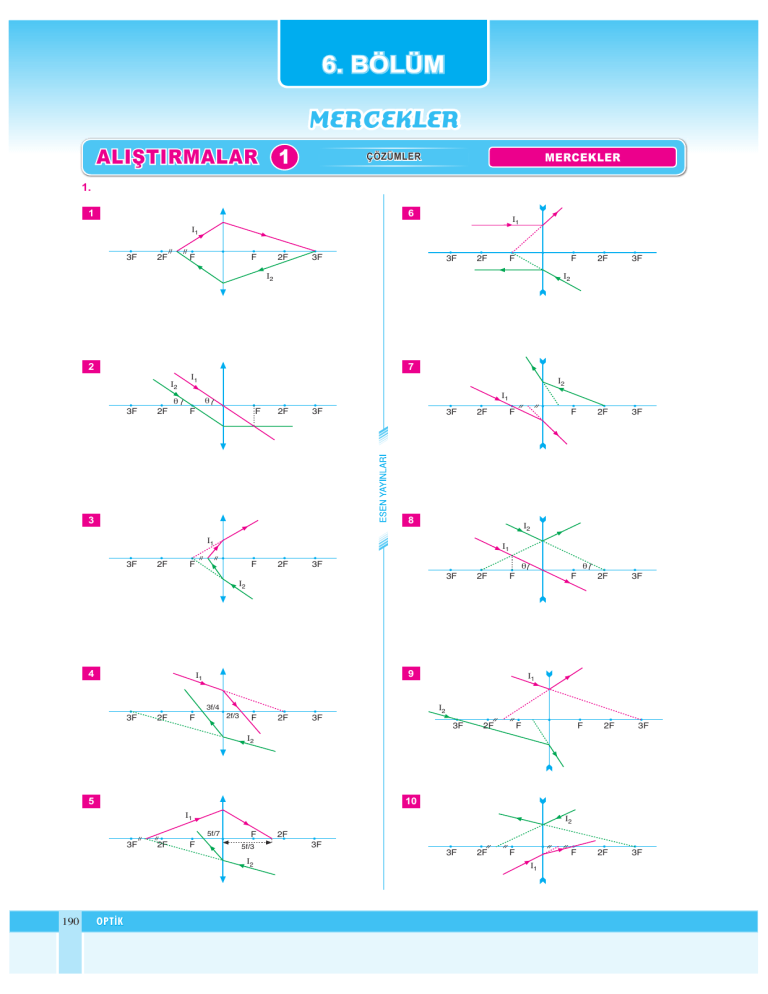
1.
1
6
I1
I1
3F
2F
F
F
2F
3F
3F
2F
F
F
2F
3F
F
2F
3F
2F
3F
I2
I2
2
7
I2
3F
2F
θ
I1
I2
I1
θ
F
F
2F
3F
3
3F
2F
F
8
I2
I1
3F
2F
I1
F
F
2F
3F
3F
I2
4
3f/4
2F
θ
F
9
I1
3F
2F
2f/3
F
F
2F
F
θ
I1
I2
3F
3F
2F
F
F
2F
3F
I2
5
10
I1
I2
5f/7
3F
2F
F
F
5f/3
I2
190
OPTİK
2F
3F
3F
2F
F
F
I1
2F
3F
2.
1
6
I
asal
eksen
I
•
•
•O
•
•
f1=4
•
asal
eksen
•
•
•
•
f2=2
O1
•
•
f1=4
•
O2
•
f2=1
7
2
I
•
•
•
•
•
O
T
•
asal
eksen •
•
asal
eksen
•
•
f2=2
f1=3/2
O1
•
•
•
•
f1=1
•
O2
•
•
f2=2
8
3
I
•
asal
eksen
•
•
•
O
•
•
•
•
•
asal
eksen
•
• T
f1=4
f2=2
f2=2
f1=1/2
9
4
.
I
asal
eksen
•
•
.
I
•O
•
•
asal
eksen
T
•
•
•O
1
f2=4/3
f1=2
f1=2
•
•O
•
2
•
T
•
•
f3=2
f2=2
10
5
I
•
•
•O
f1=1
•
•
T
•
f2=4
•
asal
eksen
asal
eksen
•
•
•
•O
1
•
•O
2
•
•
T
I
f1=3/2
f2=1/2
f3=2
OPTİK
191
3.
1
4
I
• x • x • xO • x • x • x • x • x • x •
asal
eksen
x
x
O1
I
f2
f1
x
x
x
O2
f1
Her aralığa x diyelim.
3f1
= 3x
2
f1 = 2x olur.
x
asal
eksen
f2
Her aralığa x dersek,
3
4x
f = 2x & f1 =
2 1
3
olur.
f2 = 2x
Çukur aynanın odak uzaklığı,
Buna göre, f2 > f1 dir.
f2 = 2x olur.
Buna göre, f1 = f2 dir.
5
2
•
asal
eksen
x
•
•
x
O
x
•
x
•
x
•
x
I
• T
x
x
1
2
•O •O •
f1
x
x
•
•
x
•
asal
eksen
f2
Her aralığa x diyelim.
f1
f2
f1 = 2x
1
1
1
=
+
f2 2x 4x
Her aralığa x dersek
f1 = x ,
f2 = 2x olur.
1
3
4x
=
& f2 =
f2 4x
3
Buna göre, f2 > f1 dir.
Buna göre, f1 > f2 dir.
3
I
•
•
d
•
d
f1
2d
1
1
1
=– –
f2
d 2d
1
3
2d
=
& f2 =
f2 2d
3
Aynanın odak uzaklığı;
1
1
1
– =
–
f1 3d d
–
1
2
3d
=–
& f1 =
f1
3d
2
Buna göre; f1 > f2 dir.
192
OPTİK
asal
eksen
6
•
f2
Merceğin odak uzaklığı;
–
•
x
•
x
•O
1
I
x
•
f1
x
•
•O
x
2
asal
eksen
f2
Her aralığa x diyelim. İnce kenarlı merceğin odak
uzaklığı,
2x
3f1 = 2x ⇒ f1 =
olur.
3
Kalın kenarlı merceğin odak uzaklığı,
f2 = 2x olur.
Buna göre, f2 > f1 dir.
7
10
.
•
•
x
I
•O
x
1
x
•
•O
x
2
x
•
x
asal
eksen
•
asal
eksen
•
x
•
f2
f1
x
•
O1
x
f1
Her aralığa x diyelim. İnce kenarlı merceğin odak
uzaklığı,
3
4x
f = 2x ⇒ f1 =
olur.
2 1
3
Kalın kenarlı merceğin odak uzaklığı,
•
x
•
O2
x
•
f2
x
•
O3
x
•
x
•
x
•
f3
Her aralığa x diyelim.
f1 = 2x
f2 = 4x
3
f3 = 3x ⇒ f3 = 2x olur.
2
f2 = 2x olur.
Buna göre, f2 > f1 = f3 olur.
Buna göre, f2 > f1 dir.
8
•
I
x
•
x
•
x
•
x
•
x
•
x T•
f2
f1
asal
eksen
x•
f3
Her aralığa x diyelim.
f1 = 2x
2f2 = 3x ⇒ f2 =
f3 = 2x
3
x
2
Buna göre, f1 = f3 > f2 olur.
9
asal
eksen
x
I
O1
f1
x
O2
f2
T
x
f3
Her aralığa x diyelim.
f1 = x
f2 = 2x
2f3 = 3x
3x
f3 =
olur.
2
Buna göre; f2 > f3 > f1 olur.
OPTİK
193
4.
1
6
L
K
2h
2h
3F
2F
F
F
K
K›
L
L›
2h
2h
h 2F
3f/4 2f/3
3F
3F
4h
2F
F
F
2F
3F
›
K
›
L
2
7
K
K
L
2f
3
K›
3f
4
2h
3F
2F
L
F
F
2F
›
3F
3F
2F
F
›
L
2h
2F
›
L
F
F
K
2F
›
K
2h
2h
3F
3F
2F
h
F
F
2h
9
2F
F
2F
3F
L›
K›
F
2h
2F
3F
3F
2F
F
L›
F
4h
L
5
3F
K
K
2h
3F
2F
4h
K›
4h
L
L›
L
K
2h
2h
10
K
K›
2h
L
L›
2h
2F
3F
2F
h F
L›
F h
2h
K›
194
OPTİK
3F
K›
L
4
2F
L
8
3F
F
f
›
2 L
K
3
K
3f
4
3F
3F
2F
F
F
2F
3F
ALIŞTIRMALAR 2
1.
a)
MERCEKLER
ÇÖZÜMLER
2.
K
a)
K
10cm
60cm
30cm
L
K ışınının uzantısı asal ekseni kestiğinden,
Dc= – 30cm alınarak, Dg bulunur.
1
1
1
=
+
f Dc Dg
1
1
1
=–
+
30 Dg
60
20cm
K ışınının kestiği noktada cisim, uzantısının kestiği noktada görüntüsünün olduğu düşünülerek,
Dc = 20 cm, Dg = – 30 cm alındığında,
1
1
1
=
+
f Dc Dg
1
1
1
=
+
Dg 60 30
1
1
1
–
=
f 20 30
1
1
=
D g 20
D g = 20 cm
1
1
=
f 60
olur .
f = 60 cm
Dg (+) çıktığından ışın
kı rıl dık tan
son ra,
kendisi asal ekseni
keser.
bulunur.
K
b)
Dg=20cm
L
Dg=240cm
b) L ışınının kendisi asal ekseni kestiğinden,
Dc = 90 cm alınarak, Dg bulunur.
1
1
1
=
+
f Dc Dg
1
1
1
=
+
60 90 Dg
Dg=180cm
Dc=80cm
L ışınının kestiği noktada cisim, uzantısının kestiği noktada görüntünün olduğu düşünülerek,
Dc = 80 cm, f = 60 cm alındığında,
1
1
1
=
+
f Dc Dg
1
1
1
=
–
D g 60 90
1
1
=
D g 180
1
1
1
=
+
60 80 Dg
D g = 180 cm olur.
1
1
1
=
–
D g 60 80
Dc=90cm
L
1
1
=
D g 240
D g = 240 cm
olur. Dg (+) çıktığından ışın kırıldıktan sonra, kendisi asal ekseni keser.
Dg (+) çıktığından ışın kırıldıktan sonra, kendisi
asal ekseni keser.
OPTİK
195
3.
5.
K
Dc=60cm
Hc= 6cm
2F
F
20cm
Hg
Dg=40cm
K
K›
a) Işının asal ekseni kestiği noktada cisim varmış
gibi düşünürsek, K ışını için Dc = 50 cm olur. Işın
mercekte kırıldıktan sonra uzantısının asal ekseni
kestiği noktada görüntü varmış gibi düşünürsek,
a) Görüntüsü ters olduğuna göre, ince kenarlı
mercektir. Merceğin odak uzaklığı,
1
1
1
=
+
f Dc Dg
1
1
1
=
+
f 60 40
–
1
5
=
& f = 24 cm bulunur.
f 120
–
1
1
1
=
+
f Dc Dg
1
1
1
=
+
20 50 Dg
Hc Dc
=
Hg Dg
Dg = –
6
60
=
H g 40
100
cm olur.
7
b) L ışını için,
H g = 4 cm bulunur.
–
–
4.
1
1
1
=
+
f Dc Dg
1
1
1
=
+
20 30 Dg
A
›
B
F
Sc
1
1
1
=–
–
20 30
Dg
5
1
=–
60
Dg
Dc
h
B
1
1
1
=–
–
Dg
20 50
7
1
=–
100
Dg
b) Görüntünün boyu,
2F
30cm
L
D g = –12 cm bulunur.
f
Dg=80cm
4h
A›
6.
a)
K
a) Cismin aynaya olan uzaklığı,
Hc Dc
=
Hg Dg
D
h
= c
4h 80
D c = 20 cm bulunur.
Merceğin odak uzaklığı,
1
1
1
=
+
f Dc Dg
1
1
1
=
+
f 20 80
1
5
=
f 80
f = 16 cm olur.
b) Cismin odağa olan uzaklığı,
Sc = Dc – f
Dc=5cm
Dg=10cm
K ışınının uzantısının aynaya olan uzaklığı 5 cm
olduğundan Dc = –5 cm olur. Kırılan ışının asal
ekseni kestiği nokta,
–
–
1
1
1
=
+
f Dc Dg
1 1
1
=– +
5 Dg
10
1 1
1
+
=–
10 5
Dg
1
1
=
Dg 10
Dg = 10 cm
= 20 – 16
= 4 cm bulunur.
196
OPTİK
olur. Dg (+) çıktığından ışının kendisi asal ekseni keser.
b)
8.
K
K›
L
3h
h
Dg
Dc=–30cm
Dg=–15 cm
asal
eksen
Dc=60cm
L ışınının uzantısı aynayı kestiğinden, Dc= –30 cm
alınır. Dg uzaklığı,
–
–
Hg
Hc
=
Dg
Dc
1 Dg
=
3 60
1
1
1
=
+
f Dc Dg
D g = 20 cm
1
1
1
=–
+
10
30 D g
1
1
1
=
–
f
Dc Dg
1
1
1
=
–
f
60 20
1 –2
=
f
60
f = –30 cm olur.
1
1
1
=–
+
Dg
10 30
9.
1
1
=–
Dg
15
Şekil-I de merceğin odak uzaklığı,
1 nm
1 1
=(
– 1).( + )
r r
no
f
1 nm
2
=(
– 1).
no
r
f
D g = – 15 cm
olur. Dg (–) çıktığından kırılan ışının uzantısı asal
ekseni keser.
Şekil-II de merceğin odak uzaklığı,
n
1
1 1
= ( m – 1).( + )
›
r
no
f
n
1
1
= ( m – 1).
no
r
f›
7.
' ve ( eşitlikleri taraf tarafa oranlanırsa,
n
1 d m – 1n. 2
r
f = no
1
nm
1
– 1n.
d
›
r
no
f
M
K
K›
6cm
Hg
Dg=20cm
Dc=30cm
a) Merceğin odak uzaklığı,
–
1
1
1
=
+
f Dc Dg
–
1
1
1
=
–
f 30 20
–
1
1
=–
f
60
f = 60 cm olur.
b) Görüntünün boyu,
asal
eksen
›
›
f
= 2 & f = 2f olur.
f
10. G1 gözlemcisi çukur
yüzey
gö re ce ğin den
r1 = – 20 cm, G2 gözlemcisi düz yüzey göreceğinden r2 = ∞ alınarak
işlem yapılır.
r=20cm
Gf
G2
a) n1 = 1 iken odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f1
no
r1 r2
3
1 f2
1
1
– 1 p. c –
=
+ m
f1
1
20 3
Hc Dc
=
Hg Dg
1 1
1
= .c–
+ 0m
f1 2
20
6
30
=
H g 20
1
1
=–
& f1 = – 40 cm olur.
f1
40
H g = 4 cm bulunur.
3
nm= ––
2
f1 (–) çıktığından kalın kenarlı mercek özelliği gösterir.
OPTİK
197
b) n2 = 4/3 iken merceğin odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f2
no
r1 r2
J3
N
O
1 K2
1
1
= K – 1 O. c –
+ m
20 3
f2 K 4
O
K
O
L3
P
1
9
1
= c – 1m.c–
m
f2
8
20
1 1
1
= .c–
m
f2 8
20
1
1
=–
f2
160
f2 = –160 cm olur.
f2 (–) çıktığından kalın kenarlı mercek özelliği gösterir.
11.
cm
30
r 2=
nm=4
r1 =
20
cm
O2
O1
çukur
asal
eksen
çukur
a) n1 = 3 iken merceğin odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f1
no
r1 r2
1
4
1
1
–
= c – 1m.c–
m
f1
3
20 30
1 1
1
= .c–
m
f1 3
12
1
1
=–
36
f1
f1 = – 36 cm olur.
f1 (–) çıktığından kalın kenarlı mercek özelliği gösterir.
c) n3 = 2 iken merceğin odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f3
no
r1 r2
3
1 f2
1
1
– 1 p. c –
=
+ m
2
20 3
f3
1
3
1
= c – 1m.c–
m
4
20
f3
1
1
1
= c– m.c–
m
4
20
f3
f3 = 80 cm olur.
f3 (+) çıktığından ince kenarlı mercek özelliği gösterir.
b) n2 = 4 iken merceğin odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f2
no
r1 r2
1
4
1
1
–
= c – 1m.c–
m
f2
4
20 30
f2 = 0 olur.
olur. Mercek özelliği göstermez.
c) n3 = 5 iken merceğin odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f2
no
r1 r2
1
4
1
1
–
= c – 1m.c–
m
5
20 30
f2
1
1
1
= c– m.c–
m
5
12
f3
1
1
=
f3 60
f3 = 60 cm
olur.
f3 (+) çıktığından ince kenarlı mercek özelliği gösterir.
198
OPTİK
12. a) Gözlüğün numarası (+) ise ince kenarlı, (–) ise
kalın kenarlı mercek özelliği gösterir. Gözlüğün
numarası +4 olduğundan ince kenarlı mercektir.
b) Yakınsama, bir merceğin odak uzaklığının metre cinsinden tersine denir. Doğrudan gözlük
1
numarasıdır. Birim
= diyoptridir.
m
Odak uzaklığı,
Y=
4=
1
f
1
& f = 0, 25 m = 25 cm olur.
f
14. Merceğin hava ortamında odak uzaklığı 20 cm
olduğuna göre,
n
1
1 1
= d m – 1 nd + n
f
no
r1 r2
3
1 f2
1 1
=
– 1 p. d + n
r1 r2
20
1
1
1 1 1
1 1
1
= .
+
& + =
olur.
20 2 d r1 r2 n r1 r2 10
a) n 1 =
4
ortamında odak uzaklığı,
3
n
1
1 1
= d m – 1n.d + n
f1
no
r1 r2
13.
X
Y
fX=20cm
Z
fY=30cm
fiekil-I
fsis
fiekil-II
N
J3
O 1
1 K2
= K – 1 O.
f1 K 4
OO 10
K
P
L3
1
9
1
= c – 1m.
f1
8
10
1 1 1
= .
f1 8 10
f1 = 80 cm olur.
a) X merceğinin yakınsaması,
1
1
=
= 5 diyoptri
YX =
fX 0, 2m
Y merceğinin yakınsaması,
YY =
1
1
10
=–
=–
diyoptri olur.
fY
0, 3
3
Z merceğinin yakınsaması
b) n2 = 2 ortamında odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f2
no
r1 r2
3
1 f2
1
=
– 1 p.
f2
2
10
1
1 1
= c– m.
f2
4 10
f2 = – 40 cm olur.
YZ = YX + YY
=5–
=
10
3
5
diyoptri olur.
3
b) Z merceğinin odak uzaklığı,
1
Y=
f
1
1 3
f= =
= m
Y 5 5
3
300
=
cm
5
= 60 cm
15. Merceğin odak uzaklığı, kırmızı ışınlar için 20 cm
ise,
n
1
1 1
= d m – 1 nd + n
f
no
r1 r2
1
2
1 1
= c – 1m.d + n
20
1
r1 r2
1
1 1
1 1
1
= 1. d + n & + =
olur.
20
r1 r2
r1 r2 20
bulunur.
OPTİK
199
a) Yeşil ışınlar için odak uzaklığı,
b)
n
1 1
1
= d m – 1n.d + n
r1 r2
f
no
R›
1
1
3
= c – 1m.
20
1
f
1
1
= 2.
20
f
1
1
=
f 10
f = 10 cm bulunur.
Her bir yağmur tanesinin yarıçapı R ise 8 tane
yağmur tanesinin birleştirilip yeni bir yağmur
tanesi oluşturulursa bu yağmur tanesinin yarıçapı,
8.V = V
b) Mavi ışınlar için odak uzaklığı,
n
1
1 1
= d m – 1n.d + n
f
no
r1 r2
1
4
1
= c – 1m.
f
1
20
1
1
= 3.
f
20
20
f=
cm bulunur.
3
›
›3
3
4
4
8. rR = rR
3
3
3
›3
Bu yağmur tanesi mercek gibi davrandığında
odak uzaklığı,
n
1
1
1
= d m – 1n.d
+
f
no
R1 R2 n
4
1 f3
1
1
– 1 p. c
=
+
m
1
2R 2R
f
1 1 1
= .
f 3 R
f = 3R
f = 3.2
f = 6 mm olur.
16. a) Yağmur yağarken, gök kuşağının oluşması,
ışığın, su damlalarında kırılmasının bir sonucudur. Yağmur damlasını, eğrilik yarıçapı birbirine eşit ince kenarlı mercek olarak düşenebiliriz. Yağmur damlasının kırılma indi4
si
olduğundan merceğin odak uzaklığı,
3
n
1
1
1
= d m – 1 nd
+
f
no
R1 R2 n
4
1 f3
1 1
– 1 p. c + m
=
3
1
R R
1 1 2
= .
3 3 R
1=
200
OPTİK
2
& R = 2 mm olur.
R
›
8R = R & R = 2R olur.
TEST
1
MERCEKLER
ÇÖZÜMLER
4.
1.
I
A
•
x
x
•
O
X
•
Y
x
x
•
Z
asal B •.
eksen K
asal
eksen
•
T
A›››
•
•
L B›››
•
P
B›
•
O
R
T
S
•
•
A›
B››
A››
Şekilde görüldüğü gibi, AB cisminin sistemdeki
son görüntüsü L-P arasında oluşur.
Her aralığa x diyelim. Gelen ışının uzantısı asal
ekseni kestiğinden Dc = – 4x alınır. Bu durumda,
CEVAP C
Dc = – 4x, Dg = x
olduğundan odak uzaklığı,
1
1
1
=
+
1 Dc Dg
1
1 1
=–
+
4x x
f
5.
1
3
=
f 4x
f=
I
4x
olur.
3
asal
eksen
•
•
x
x
•
•O
x
Buna göre, ince kenarlı merceğin odak noktası
X-Y arasındadır.
CEVAP A
x
•
x
f1
•
x
• T
f2
Her aralığa x diyelim.
2.
I2
asal
eksen
f1 = 3x
›
I1
X
3
f = 3x
2 2
I1
I3
F
•
•O
•
›
f2 = 2x
›
f1 3x 3
=
=
olur.
f2 2x 2
I2
F
I3
CEVAP C
Y
f
Ι1 ve Ι2 ışık ışınları Y düzlem aynasından yansır.
CEVAP B
3.
6.
A
asal B •
eksen
2F
•
F
•
O
•
F
K
X
•
•›››
2F
•
K
f
›
•
Y
f
•
Z
f
•
O
U
f
K
f
››
K
• T
•
f
4
AB cisminin ince kenarlı mercekteki görüntüsü 4
numaralı görüntüdür.
CEVAP D
Şekilde görüldüğü gibi, K ışık kaynağının
sistemdeki son görüntüsü X noktasında oluşur.
CEVAP A
OPTİK
201
7.
10.
•
•
•O
•
I
•
•
T
d
asal
eksen
•
2f2
3f1
f1
f2
CEVAP D
8.
F
•
•
•
I
.
•
F
•O •
•
•
2F
•
•
asal
3F eksen
f
İnce kenarlı merceğe 1,5f den gelen ışın kırıldıktan
sonra 3f den geçerek kırılır. Işın düzlem aynadan
yansıdıktan sonra merceğe uzantısı –f den geçef
cek şekilde geldiğinden kırıldıktan sonra
den
2
geçerek kırılır.
CEVAP E
9.
I
asal
eksen
•
•
• T
•
O
2f1
d
f1
2f2
f2
Şekilde görüldüğü gibi, mercekler arasındaki d
uzaklığı,
d = 2f2 – 2f1
d = 2(f2 – f1) olur.
CEVAP E
202
OPTİK
•O
f
•
T•
f
f
f
d = 3f1 – 2f2 olur.
2F
•
I
Şekilde görüldüğü gibi, ince kenarlı mercek ile
tümsek ayna arasındaki d uzaklığı,
•
asal
eksen
•
f
f
Mercek ve tümsek aynanın odak uzaklıkları eşit
olduğundan ışın şekildeki yolu izleyerek sistemi
terk eder.
CEVAP B
TEST
2
MERCEKLER
ÇÖZÜMLER
1.
4.
I
K
•O
ı
K
•O
1
ıı
K
2
asal
eksen
•
•
O1
O2
•
f/2
f2
2f
2f
f
2f
f
f
5f
asal
eksen
•
f2
Kalın kenarlı merceğin odak uzaklığının büyüklüğü,
Şekilde görüldüğü gibi, noktasal K ışıklı cisminin
düzenekteki son görüntüsü kendisinden 5f kadar
uzakta oluşur.
f2 = 2f –
f 3
= f olur.
2 2
CEVAP B
CEVAP D
5.
2.
A
A
I
B.
•
K F
•O1
•O2
n1
no
n2
asal
•
L eksen
•
O
B.
•
K
asal
•
L eksen
•O
asal
eksen
fiekil-I
.
fiekil-II
Şekil-I de:
K noktası, merceğin odak noktasıdır.
İnce kenarlı, kalın kenarlı merceklerin ve saydam ortamın ışığı kırma indisleri n1, n2, no arasında n1 > no > n2
ilişkisi vardır.
Şekil-II de:
1
1 1
= +
fsis f f
CEVAP A
1
2
f
=
& fsis =
olur.
fsis f
2
3.
K
K›
•
•
10 cm 20 cm
•
K noktası, sistemin 2F noktasıdır.
.
•
30cm
f1 = 20 cm
f2 = 30 cm
X
60cm
Buna göre, AB ışıklı cisminin görüntüsü L noktasında oluşur.
asal
• eksen
CEVAP A
K››
6.
ı
A
ı
K cisminin tümsek aynadaki görüntüsü K olur.
ı
K nün ince kenarlı mercekteki görüntüsü ise;
A
asal
3F
ı
eksen B •
1
1
1
=
+
30 60 D g
f
1
1
1
–
=
30 60 D g
D g = 60 cm
•
B
olur.
.
2F
•O
•
ıı
X B
F
•
Y
•Z
•
T
ıı
A
Y noktası çukur aynanın odak noktasıdır.
ı
ı
K cisminin görüntüsü X noktasında olur. K nin X
noktasındaki görüntüye olan uzaklığı ise;
30 + 60 = 90 cm olur.
CEVAP E
ı
A B çukur ayna için cisim olacağından görüntüsü
1,5 f de olur.
Şekilde görüldüğü gibi, AB ışıklı cisminin çukur
aynadaki görüntüsü X noktasında oluşur.
CEVAP A
OPTİK
203
7.
9.
I1 ışık ışının izlediği yol yanlış çizilmiştir.
K
I1
K
M
Dc
2F h
2F
F
F
asal
eksen
Dg=4Dc
4h
100cm
ı
K
Hg
1br
Hc
Şekil-I deki sistemin odak uzaklığı,
1
fsis
=
Dg
=
Dc
4 100 – D c
=
1
Dc
1 1
+
f1 f2
4Dc = 100 – Dc
1
1 1
1
= + & fsis = br olur.
fsis 1 1
2
5Dc = 100
I1 ışık ışınının izlediği yol şekildeki gibidir.
Dc = 20 cm
I2 ve I3 ışık ışınlarının izledikleri yollar doğru çizilmiştir.
CEVAP D
Dg = 80 cm
8.
Merceğin odak uzaklığı,
1
1
1
=
+
f Dc Dg
A
A
Hc
Hg
ı
B .
F•sis
Dg
.
B
Dc
1
1
1
=
+
f 20 80
ı
•O
Y1
F•sis
asal
eksen
1
5
=
& f = 16 cm olur.
f 80
CEVAP E
Y2
L
K
10.
Sistemin yakınsaması,
I1
Y = Y1 + Y2
asal
eksen
Y = –5 + 3
Y = –2 diyoptri
Sistemin odak uzaklığı,
Y=
fiekil-I
1
fsis
1
–2=
fsis
L
I2
2
K
asal
eksen
fsis = –0,5 m = –50 cm olur.
Görüntünün sisteme olan uzaklığı,
Hg
Hc
=
Dg
fiekil-II
Dc
Dg
K merceğinin odak uzaklığı, fK = 2 br,
1
=
3 Dc
D
D g = c olur.
3
L merceğinin odak uzaklığı, fL = 1 br olur.
Sistemin odak uzaklığı,
1
1
1
=
–
fsis fK fL
1
1 1
= –
fsis 2 1
1
1
=–
fsis
2
fsis = –2 br olur.
Cismin sisteme olan uzaklığı,
1
1
1
– =
–
f Dc Dg
1
1
3
=
–
–
50 D c D c
1
–2
=
–
50 D c
D c = 100 cm olur.
Buna göre, I2 ışık ışını 2 yolunu izler.
CEVAP B
204
OPTİK
CEVAP B
11. Y = –2,5 diyoptri
f=?
Gözlük camının odak uzaklığı,
1
Y=
f
1
f
f = –0,4 m
–2,5 =
f = – 40 cm olur.
CEVAP C
12.
A
Dc=60cm
A
›
Dg
F
asal
eksen
B
•
B
f
Hg
Hc
=
F
•
•O
›
f
Dg
Dc
1 Dg
=
4 60
Dg = 15 cm olur. Merceğin odak uzaklığı;
1
1
1
=
–
f Dc Dg
1
1
1
=
–
f 60 15
1
3
=–
f
60
f = – 20 cm olur.
CEVAP C
OPTİK
205
