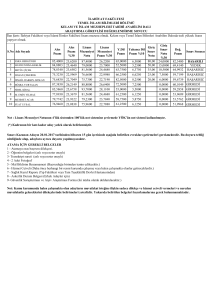
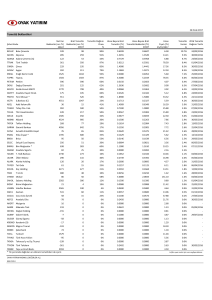
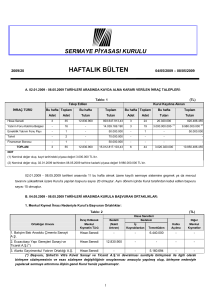
1. Ders
Ön Bilgiler
>> veri=[1 2 3
456
642
1 0 1]
veri =
1 2 3
4 5 6
6 4 2
1 0 1
>> mean(veri)
ans =
3.0000 2.7500
3.0000
>> kron(ones(4,1),mean(veri))
ans =
3.0000 2.7500 3.0000
3.0000 2.7500 3.0000
3.0000 2.7500 3.0000
3.0000 2.7500 3.0000
>> ortsapveri=(eye(4)-1/4*ones(4,4))*veri
ortsapveri =
-2.0000 -0.7500
0
1.0000 2.2500 3.0000
3.0000 1.2500 -1.0000
-2.0000 -2.7500 -2.0000
>> veri-kron(ones(4,1),mean(veri))
ans =
-2.0000
1.0000
3.0000
-2.0000
-0.7500
0
2.2500 3.0000
1.2500 -1.0000
-2.7500 -2.0000
>> std(veri)
ans =
2.4495 2.2174
2.1602
>> stveri=ortsapveri./kron(ones(4,1),std(veri))
stveri =
-0.8165 -0.3382
0
0.4082 1.0147 1.3887
1.2247 0.5637 -0.4629
-0.8165 -1.2402 -0.9258
>> cov(veri)
ans =
6.0000 4.3333
4.3333 4.9167
1.3333 3.6667
1.3333
3.6667
4.6667
>> cov(ortsapveri)
ans =
6.0000 4.3333
4.3333 4.9167
1.3333 3.6667
1.3333
3.6667
4.6667
>> cov(stveri)
ans =
1.0000 0.7978
0.7978 1.0000
0.2520 0.7655
0.2520
0.7655
1.0000
>> corr(stveri)
ans =
1.0000 0.7978
0.7978 1.0000
0.2520 0.7655
0.2520
0.7655
1.0000
>> corr(veri)
ans =
1.0000 0.7978
0.7978 1.0000
0.2520 0.7655
0.2520
0.7655
1.0000
>> cov(veri)
ans =
6.0000 4.3333
4.3333 4.9167
1.3333 3.6667
1.3333
3.6667
4.6667
Ön Bilgiler
( R, +,.) reel sayılar cismi olsun. Kısaca R ile gösterilsin.
R n = {(a1 , a 2 ,..., a n ) : ai ∈ R , i = 1,2,..., n}
reel sayıların sıralı n-lilerinin kümesi olsun. R n kümesi,
⊕ : Rn × Rn → Rn
(a1 , a 2 ,..., a n ) ⊕ (b1 , b2 ,..., bn ) = ((a1 + b1 , a 2 + b2 ,..., a n + bn )
ve
• : R × R n → Rn
c • ( a1 , a2 ,..., an ) = ( ca1 , ca2 ,..., can )
işlemleri altında R cismi üzerinde bir vektör uzayıdır, yani:
a) ( R n , ⊕) bir Abel grubu,
b) c1, c2 ∈ R ve a = (a1, a2 ,..., an ) , b = (b1, b2 ,..., bn ) ∈ R n için
i) ( c1.c2 ) • a = c1 • ( c2 • a )
ii) ( c1 + c2 ) • a = (c1 • a) ⊕ ( c2 • a )
iii) c1 • (a ⊕ b) = (c1 • a) ⊕ ( c1 • b )
iv) 1 • a = a
özellikleri sağlanmaktadır. Bu uzayı ( Rn , R , ⊕ , • ) veya R1×n ile gösterelim. R1×n
vektör uzayının elemanlarına n-bileşenli satır vektörleri denir.
Rn×1 kümesi,
a1
n×1 a2
R =
: a1, a2 ,..., an ∈ R
⋮
an
olmak üzere,
⊕ : Rn×1 × Rn×1 → Rn ×1
a1 b1 a1 + b1
a2 ⊕ b2 = a2 + b2
⋮ ⋮ ⋮
an bn an + bn
ve
• : R × Rn×1 → Rn×1
a1 ca1
a
ca
c • 2= 2
⋮ ⋮
an can
işlemleri altında Rn×1 bir vektör uzayıdır. Bu uzayın elemanlarına n-bileşenli sütun
vektörleri denir.
Rn×1 ‘in elemanlarını, altına bir çizgi atılmış küçük veya büyük harflerle
göstereceğiz.
a1
X1k
a2
X 2k
∈ R n×1
a=
, Xk =
⋮
⋮
an
X nk
R1×n ‘in elemanlarını
a ' = ( a1 , a 2 ,..., a n )
X 'k = ( X k 1 , X k 2 ,..., X kn )
biçiminde göstereceğiz.
R1×n ile Rn×1 uzayları farklı iki vektör uzayıdır. Rn , R1×n veya Rn×1 söz knusu
olduğunda hangisinden bahsedildiği açık olarak anlaşılıyorsa üçü de Rn ile
gösterilecektir. Özel olarak Rn standart vektör uzayı dendiğinde, Rn×1 söz konusu
olacağını belirtelim.
Rn×m kümesi n × m boyutlu reel elemanlı matrislerin kümesi olmak üzere
matris toplamı ve matrislerin skalar ile çarpımı işlemleri altında Rn×m kümesi R
üzerinde bir vektör uzayıdır.
Tanım V bir vektör uzayı olmak üzere ,
. :V→R
v→ v
fonksiyonu:
i ) ∀v ∈V için v ≥ 0
ii )
v =0⇔v=0
iii ) ∀a ∈ R ve ∀v ∈V için
av = a . v
iv ) ∀u , v ∈V için
u+v ≤ u + v
özelliklerini sağladığında, . fonksiyonuna norm , v sayısına v vektörünün normu,
(V , . ) ikilisine de normlu vektör uzayı denir.
Norm, bir vektör uzayındaki vektörlere pozitif bir reel sayı karşılık getiren bir
fonksiyondur. Bir vektörün normu, geometrik olarak, vektörün uzunluğu olarak
yorumlanmaktadır.
Örnek Rn standart vektör uzayında, a ∈ R n için,
1)
m
a = max a1 , a2 ,..., an
n
r
p
2)
a = ( ∑ ai )1/ p
3)
a = ( ∑ ai2 )1/ 2
, p ≥ 1 ( l p normu)
i =1
n
i =1
,
( Euclide normu)
olarak tanımlı . : R n → R fonksiyonları birer normdur.
Örnek Rn×m vektör uzayında A = ( aij ) ∈ Rn × m için,
n
a)
A 1 = max( ∑ aij )
i =1
n
j
b)
A ∞ = max( ∑ aij )
i
j =1
c)
A 2 = ( A′ A nýn en büyük özdeðeri)1/ 2
d)
A E = ( ∑ ∑ aij2 )1/ 2
n
n
i =1 j = 1
n
A = ∑ ∑ aij
i =1 j =1
n
e)
{
}
f ) A = max aij : i = 1, 2 ,..., n , j = 1, 2 ,..., m
olarak tanımlı fonksiyonlar birer normdur.
Tanım V bir vektör uzayı olmak üzere,
< .,. > : V × V → R
(u, v) →< u , v >
fonksiyonu :
i ) < u , v >=< v , u >
ii ) a , b ∈ R için,
< au + bv , z >= a < u , z > + b < v , z >
iii ) v ≠ 0 için < v, v >
>
0 , v = 0 için < v, v >= 0
özelliklerini sağladığında, < u, v > sayısına u ile v ‘nin iç çarpımı ve (V , <.,. > )
ikilisine de iç çarpım uzayı denir.
Örnek Rn standart vektör uzayında a , b ∈ R n için ,
n
< a, b >= ∑ a i bi = a ' b
i =1
olarak tanımlı <.,. > fonksiyonu bir iç çarpımdır. Bu iç çarpıma Öklid (Euclide) iç
çarpımı denir. Bu iç çarpım ile birlikte Rn standart vektör uzayına Öklid uzayı
denir.
Rn×m de A , B ∈ Rn × m için
n
m
< A , B >= ∑ ∑ aijbij
i = 1 j =1
olarak tanımlı <.,. > fonksiyonu bir iç çarpımdır.
Teorem (V , <.,. > ) bir iç çarpım uzayı olmak üzere,
( < u , v > )2 ≤< u , u >< v , v >
dır (Cauchy-Schwartz Eşitsizliği).
Đspat: http://en.wikipedia.org/wiki/Cauchy-Schwarz_inequality
Sonuç: Cauchy-Schwarz Eşitsizliği
(< u , v >) 2 ≤< u , u >< v, v >
2
< u, v >
≤1
< u , u >< v, v >
< u, v >
≤1
< u , u >< v, v >
olmak üzere, R n +1 Euclide uzayında x, y ∈ R n+1 için,
n
< x, y >= ∑ xi yi = x ' y
i =1
olup,
n
∑x y
i
i =1
n
i
∑x ∑y
i =1
≤1
n
2
i
i =1
2
i
dır. Ortalamadan sapmalar şekline getirilen (merkezileştirilmiş) vektörler,
x1 − x
y1 − y
x − x
, y* = y2 − y ∈ R n×1
x* = 2
⋮
⋮
xn − x
yn − y
olmak üzere, bunlar için Cauchy-Schwartz Eşitsizliği
n
∑ ( xi − x )( yi − y )
i =1
n
n
i =1
i =1
≤1
∑ ( xi − x )2 ∑ ( yi − x )2
biçimindedir. Buna göre, örneklem korelasyon katsayısı olarak bildiğimiz,
n
∑ ( xi − x )( yi − y )
i =1
r=
n
n
i =1
i =1
∑ ( xi − x )2 ∑ ( yi − x )2
değeri,
r ≤1
−1 ≤ r ≤ 1
dır.
Teorem (V , <.,. > ) bir iç çarpım uzayı olmak üzere <.,. > iç çarpım yardımıyla
tanımlı,
. < , > :V → R
1
u → u < ,> = ( < u, u > ) 2
fonksiyonu V de bir normdur.
Bir iç çarpım uzayında ayrıca bir norm verilmemişse norm olarak bu iç çarpıma
dayalı . < , > normu söz konusu olacaktır ve gösterim olarak sadece . yazılacaktır.
Tanım: (V , <.,. > ) bir iç çarpım uzayı olmak üzere,
cos( u , v ) =
< u, v >
u v
sayısına u ile v vektörleri arasındaki "açının kosinüsü" denir.
Normları sıfırdan farklı iki u ile v vektörleri için < u , v >= 0 ise bu vektörlere
dik (ortogonal) vektörler denir ve u⊥ v biçiminde gösterilir. V ‘nin V1,V2
altkümelerinde ∀u ∈ V1 ve ∀v ∈ V2 vektörleri için u⊥ v ise V1 kümesine V2 ye diktir
denir ve V1 ⊥ V2 biçiminde gösterilir.
R n×1 Euclide uzayında a, b ∈ R n için,
n
< a, b >= ∑ ai bi = a ' b
i =1
olmak üzere, bu uzayda iç çarpıma dayalı norm,
a = (< a , a > )
1
n
2
= (∑ a i2 )
1
2
= (a' a )
1
2
i =1
ve a , b vektörleri arasındaki açının kosinüsü,
n
cos( a , b) =
∑ aibi
i =1
n
1
( ∑ ai2 ∑ bi2 ) 2
i =1 i =1
n
dır.
R3×1 Euclide uzayında,
2
0
a = 2 , b = 0 ∈ R3×1
0
3
için
dır.
Tanım M boş olmayan bir küme olmak üzere,
d: M × M → R
fonksiyonu,
i) d ( x, y) ≥ 0
ii ) d ( x , y ) = 0 ⇔ x = y
iii ) d ( x , y ) = d ( y , x )
iv ) d ( x , z ) ≤ d ( x , y ) + d ( y , z )
özelliklerini sağladığında, d fonksiyonuna M kümesinde metrik, ( Μ , d ) ikilisine
metrik uzay ve d ( x , y ) sayısına x ile y elemanları arasındaki uzaklık denir.
Örnek R reel sayılar kümesinde,
d ( x, y) = x − y
olarak tanımlı d fonksiyonu bir metriktir.
Örnek (V , . ) bir normlu vektör uzayı olmak üzere,
d (u, v ) = u − v
olarak tanımlı d fonksiyonu V de bir metriktir.
Örnek R3×1 Euclide uzayında a , b ∈ R3×1vektörleri için,
3
d ( a , b) = b − a = ( ∑ (bi − ai )2 )1 2
i =1
olsun. d ( a , b) sayısı, a ile b vektörleri arasındaki uzaklık yerine, a ile b vektörlerine
karşılık gelen A ile B noktaları arasındaki uzaklık olarak yorumlanmaktadır (örnek
olarak yukarıdaki şekle bakınız).
Matrisler
Elemanları reel sayı olan matrisler,
a11 a12 ⋯ a1m
a
a22 ⋯ a2 m
A = 21
⋮
⋮
⋮
an1 an 2 … anm
biçiminde olup, kısaca A = ( aij )n×m olarak da ifade edilmektedirler. Bir A matrisinin
boyutları ile birlikte A n×m , A : n × m biçiminde de gösterilmektedir.
vektör uzayının bir bazı v1 , v2 ,..., vm olsun. Bir A : V → W lineer
dönüşümünün bilinmesi demek v1 , v2 ,..., v m baz vektörlerinin dönüşümleri olan
V
m
r
A ( v1 ), A ( v2 ),..., A ( vm ) ∈W
vektörlerinin bilinmesi demektedir. j = 1, 2 ,..., m için
A ( v j ) ∈W olmak üzere, W ‘deki baz vektörlerinin lineer bileşimi olarak,
A ( v j ) = a1 j w1 + a2 j w2 + ... + anj wn
biçiminde yazılsın.
a11 a12 ⋯ a1m
a
a22 … a2 m
21
A=
⋮
⋮
⋮
an1 an 2 ⋯ anm
matrisine A lineer dönüşümüne karşılık gelen matris denir.
Rm×1 ‘den Rn ×1 'e tanımlı bir A lineer dönüşümüne standart bazlara göre
karşılık gelen matris n × m boyutlu A matrisi ise, bir v ∈ Rm ×1 vektörünün görüntüsü
A matrisi ile v vektörünün çarpımı olan,
A(v) = Av
vektörüdür. A lineer dönüşümünün değer kümesi, bu lineer dönüşüme karşılık
gelen A matrisinin sütun vektörlerinin gerdiği alt uzaydır.
Bir A matrisinin sütun vektörlerinin gerdiği uzayı R( A) veya [ A ] biçiminde
göstereceğiz.
Mstrislerin Genelleştirilmiş Đnversleri
1955 yılında Penrose ∀A : n × m matrisi için ( A reel sayı elemanlı) aşağıdaki
denklemleri sağlayan bir tek G matrisinin var olduğunu ispatlamıştır.
1) AGA = A
3) ( AG ) ′ = AG
2) GAG = G
4) ( GA) ′ = GA
Bu dört koşulu sağlayan G matrisi Moore tarafından da incelenmiş olup bu matrise
Moore-Penrose genelleştirilmiş inversi denir ve A + ile gösterilir.
Yukarıdaki koşullardan sadece birinci koşulu sağlayan matrislere 1 -koşullu
lq
inversler denir. Bir A matrisinin 1 -koşullu inversi
gösterilir.
lq
−
A
c
g
veya A , A biçiminde
Teorem Ax = g denklem sistemini göz önüne alalım.
a) Denklem sisteminin tutarlı olması için gerek ve yeter şart
AA − g = g
olmasıdır.
b) Denklem sistemi tutarlı olsun. x 0 = G g nin bir çözüm olması için gerek ve
yeter şart G matrisinin A nın bir 1 -koşullu inversi olmasıdır.
c) Denklem sistemi tutarlı olsun. z isteksel bir vektör olmak üzere,
lq
x = A − g + ( I − A − A) z
denklem sisteminin bir çözümüdür.
Moore-Penrose Tipi Đnverslerin Bazı Özellikleri
Moore-Penrose tipi genelleştirilmiş inversleri ile ilgili bazı özellikler aşağıda
özetlenmiştir.
1) Eğer A karesel ve singüler olmayan bir matris ise
A + = A −1
dır.
2) A: n × m ve rank(A) = m , yani A nın sütun vektörleri lineer bağımsız ( A tam sütun
ranklı) ise,
A + = ( A ′ A ) −1 A ′
dır. A + matrisi A nın sol inversidir.
3) A: n × m ve rank(A) = n , yani A tam satır ranklı ise,
A + = A ′ ( A ′ A ) −1
dır. A + matrisi A nın sağ inversidir.
4) A:1 × 1 tipinde bir matris, yani A = a , a ∈ R ise,
[ 0] , a = 0
A = 1
a , a ≠ 0
+
dır. a ∈ R reel sayısı için,
a
+
R|0
= S1
|T a
,a = 0
,a ≠ 0
olarak tanımlansın.
5) A köşegen matris yani,
d1
0
A=
⋮
0
0
d2
⋮
0
0
⋯ 0
⋮
⋯ dn
⋯
ise,
d1+
0
+
A =
⋮
0
dır.
0 ⋯ 0
d 2+ ⋯ 0
⋮
⋮
0 ⋯ d n+
6) A: n × 1 tipinde bir vektör, yani A = a ∈ R n ×1 ise,
a + = (a' a)+ a'
dır.
7) A simetrik ve idempotent, yani A′ = A ve A2 = A ise A + = A dır.
8) ( A + ) + = A
( A′ ) + = ( A + ) ′
dır. Eğer
A ′ = A ise ( A + ) ′ = A + dır.
9)
A
simetrik
ise
A+
de
simetriktir,
10) A + = ( A ′ A ) + A ′ = A ′ ( AA ′ ) +
R| A′ = A′ AA + = A + AA′
|
11) S R ( A ) = R ( AA ′ ) = R ( AA + )
|| R ( A + ) = R ( A′ ) = R ( A + A) = R ( A′ A)
T
12) a , b ∈ R n için ( ab ' ) + = ( a a ' ) + ( b ' b ) + ba ' dır.
13) Herhangi bir A: n × m, rank( A) = r matrisi için,
A = BC
( B: n × r , C: r × m, rank( B ) = rank( C ) = r ) biçiminde yapılan ayrışım altında,
A + = C + B + = C ′ ( CC ′ ) −1 ( B ′ B ) −1 B ′ = C ′ ( B ′ A C ′ ) −1 B ′
dır.
14) A: n × m ve P: n × n , Q: m × m ortogonal matrisler olmak üzere,
( PAQ ) + = Q′A + P ′
dır.
15) A: n × n , A′ = A ve A nın spektral ayrışımı,
A = PDP ′
olmak üzere,
A + = PD+ P ′
dır.
A
16) A = 11
0
0
A11+
+
ise A =
A22
0
0
dır.
A22+
yani
17) ( A ⊗ B ) + = A + ⊗ B +
Elemanları 1 olan
J n× m
1
1
=
⋮
1
n×m
tipinde matris,
1 ⋯ 1
1 ⋯ 1
⋮
⋮
1 ⋯ 1
1
1
= ⊗ [1 1 ⋯ 1]1×m
⋮
1 n×1
olmak üzere,
+
J n+×m
1
1
1
+
= ⊗ [1 1 ⋯ 1]1×m = 1 1 L
⋮
n
1 n×1
LM1OP
1 1
1
1 1× n ⊗ M P
=
Jm× n
m M MP
n. m
MN1PQ
m ×1
dır.
18) (V , < , > ) bir iç çarpım uzayı, M , V ‘nin bir alt uzayı,
V =M ⊕M⊥
( M + alt uzayı M 'nin dik tümleyenidir)
ve v ∈V için,
v = vˆ + eˆ , vˆ ∈ M , eˆ ∈ M ⊥
olmak üzere M üzerine dik izdüşüm dönüşümü olan
PM : V → M
v → PM (v) = vˆ
dönüşümü bir lineer dönüşümdür. PM ye karşılık gelen matris
simetrik bir matristir, yani PM2 = PM = PM' dır.
X ⊂ R n alt uzayı üzerine dik izdüşüm matrisi,
P X = XX +
[X ]⊥ ⊂ R n alt uzayı üzerine dik izdüşüm matrisi,
P[ X ]⊥ = I − XX +
dır.
19) ( AB) + = ( PR ( A′) B)+ ( APR ( B ) )+ = ( A+ AB)+ ( ABB + ) +
20) A: n × m , B: m × k , rank ( A ) = rank ( B ) = m ise,
( AB ) + = B + A +
dır.
idempotent ve
21) y ∈ R n , X : n × p , rank ( X ) = p , (n > p) olmak üzere,
y−Xβ
2
= ( y − X β ) '( y − X β )
ifadesini en küçük yapan β vektörü,
βˆ = X + y = ( X ' X ) −1 X ' y
dır.
22)
y ∈ R n , X : n × p , rank ( X ) < p (n > p ) olmak üzere,
min y − X β = y − X β
*
β
⇔ β = X + y + (I − X + X )z , z ∈ R p
*
{
}
min β * : β * = X + y + ( I − X + X ) z , z ∈ R p = X + y
β
dır.
23) A x = b denkleminin çözümünün var olması için gerek ve yeter şart,
AA + b = b
olmasıdır. Varsa, çözümler,
x 0 = A+b + ( I − A+ A ) z , z ∈ R p isteksel vektör
biçimindedir. x = A+b çözümü, çözümler arasında minimum normludur.
Özdeğerler, Özvektörler ve Spektral Ayrışım
A: n × n tipinde reel sayıların bir matrisi olmak üzere, λ ‘ya göre bir polinom
denklemi olan, det A − λI = 0 denklemine A ‘nın karakteristik denklemi ve
b
g
köklerine A ‘nın özdeğerleri denir.
v ≠ 0 için Av = λ v oluyorsa v vektörüne λ özdeğerine karşılık gelen özvektör
denir. Bir özdeğere birden çok özvektör karşılık gelebilir.
A: n × n matrisi simetrik olduğunda:
a) Özdeğerleri reel sayılardır. Rank ( A ) = r ise 0 sayısı n - r katlı özdeğerdir.
λ 1 ≠ λ 2 özdeğerlerine karşılık gelen Av = λ1 v , Aw = λ 2 w özvektörleri için v⊥ w dır.
b) A matrisinin rankı sıfırdan farklı özdeğerlerin sayısına (katlı özdeğerler katı
kadar sayılmak şartıyla ) eşittir.
c) A nın özdeğerleri λ1 , λ 2 ,..., λ n ve
λ1 0 ...... 0
0 λ ....... 0
2
D=
.
0 0 ....... λn
b
g
olsun. P: n × n ortogonal matrisi
P′P = I A ‘nın normlanmış özvektörlerinin
matrisi (eşit özdeğerler için karşılık gelen özdeğer uzayının ortonormal baz
vektörleri) olmak üzere,
AP = DP
A = PDP′
dır.
n
A = PDP′ = ∑ λ i v i v i'
i =1
gösterimine A matrisinin spektral ayrışımı (spectral decomposition) denir.
n
A 2 = ∑ λ2i v i v i'
i =1
olmak üzere, biçimsel olarak, c ∈ R için,
n
A c = ∑ λci v i v i'
i =1
veya
n
f ( A ) = ∑ f ( λ i ) v i v i'
i =1
gibi gösterimler operatör hesabında kullanılmaktadır.
Bir komut sayfası üzerinde komutlar yazılarak kullanacağımız yazılımlar:
Scilab (Matlab’ın ücretsiz türevlerinden bir tanesi)
Veri giriş panelli ve menülü bazı yazılımlar:
Minitab
Selçuk STAT
SelçukStat (Selçuk Üniversitesi tarafından geliştirilen istatistik paket programı )
Matlab: MATLAB® (MATrix LABoratory – Matris Laboratuarı) temel olarak teknik ve
bilimsel hesaplamalar için 1970 ‘lerin sonunda Cleve Moler tarafından yazılmaya başlanmış
yüksek performansa sahip bir yazılımdır.
Matlab Masaüstü Ortamı
Menü Çubuğu
Defoult Matlab Masaüstü Görüntüsü: Workspace, Command Window, Comand History
Yukarıdaki çalışma alanı (Workspace) boş.
Aşağıdaki komut penceresi, çalışma alanı ve komut tarihçesine göz atın.
Çalışma alanı’ndaki B nesnesine tık’landıktan sonra Array Editor karşımıza çıkmaktadır.
Array Editor’de düzeltme, giriş, düzenleme yapabiliriz.
Yardım:
Statistics Toolbox
Yukarıda mean fonksiyonunu tıklayıp yardım alalım.
Aynı yardım bilgisine Komut Penceresinde
>> help mean
yazılarak da ulaşılabilir.
Matlab’ da istatistik Toolbox içerisinde bulunan fonksiyonların listesi
addedvarplot
aoctool
betalike
binoinv
boxplot
caseread
chi2gof
cluster
corr
dcovary
ecdfhist
evpdf
expinv
fcdf
frnd
gaminv
geoinv
gevfit
gline
gpcdf
gprnd
hist
hmmtrain
hygernd
iwishrnd
kstest2
linkage
lognrnd
manovacluster
moment
nanmax
nanvar
nbinstat
nctcdf
ncx2inv
nlparci
normpdf
pareto
perms
poisstat
princomp
random
raylfit
refcurve
robustfit
schart
statget
tabulate
tinv
treeval
unidcdf
unifinv
vartest
wbllike
x2fx
andrewsplot
barttest
betapdf
binopdf
candexch
casewrite
chi2inv
clusterdata
corrcoef
dendrogram
errorbar
evrnd
explike
ff2n
fstat
gamlike
geomean
gevinv
glmdemo
gpfit
gpstat
hist3
hmmviterbi
hygestat
jbtest
kurtosis
logncdf
lognstat
mdscale
multcompare
nanmean
nbincdf
ncfcdf
nctinv
ncx2pdf
nlpredci
normplot
partialcorr
poisscdf
polyconf
probplot
randsample
raylinv
refline
rotatefactors
signrank
statset
tblread
tpdf
trimmean
unidinv
unifit
vartest2
wblpdf
xbarplot
anova1
bbdesign
betarnd
binornd
candgen
ccdesign
chi2pdf
cmdscale
cov
dfittool
evcdf
evstat
exppdf
finv
fsurfht
gampdf
geopdf
gevlike
glmfit
gpinv
grp2idx
histfit
hougen
icdf
kmeans
leverage
lognfit
lsline
mean
mvnpdf
nanmedian
nbinfit
ncfinv
nctpdf
ncx2rnd
normcdf
normrnd
pcacov
poissfit
polyfit
procrustes
randtool
raylpdf
regress
rowexch
signtest
std
tblwrite
treedisp
trnd
unidpdf
unifpdf
vartestn
wblplot
zscore
anova2
betacdf
betastat
binostat
canoncorr
cdf
chi2rnd
combnk
coxphfit
disttool
evfit
ewmaplot
exprnd
fpdf
fullfact
gamrnd
geornd
gevpdf
glmval
gplike
grpstats
hmmdecode
hygecdf
inconsistent
kruskalwallis
lhsdesign
logninv
mad
median
mvnrnd
nanmin
nbininv
ncfpdf
nctrnd
ncx2stat
normfit
normspec
pcares
poissinv
polytool
qqplot
range
raylrnd
regstats
rsmdemo
silhouette
stepwise
tcdf
treefit
tstat
unidrnd
unifrnd
wblcdf
wblrnd
ztest
anovan
betafit
binocdf
biplot
capable
cdfplot
chi2stat
cophenet
crosstab
dummyvar
evinv
expcdf
expstat
fracfact
gamcdf
gamstat
geostat
gevrnd
glyphplot
gplotmatrix
gscatter
hmmestimate
hygeinv
invpred
ksdensity
lhsnorm
lognlike
mahal
mle
mvtrnd
nanstd
nbinpdf
ncfrnd
nctstat
nlinfit
norminv
normstat
pdf
poisspdf
polyval
quantile
ranksum
raylstat
ridge
rstool
skewness
stepwisefit
tdfread
treeprune
ttest
unidstat
unifstat
wblfit
wblstat
ansaribradley
betainv
binofit
bootstrp
capaplot
chi2cdf
classify
cordexch
daugment
ecdf
evlike
expfit
factoran
friedman
gamfit
geocdf
gevcdf
gevstat
gname
gppdf
harmmean
hmmgenerate
hygepdf
iqr
kstest
lillietest
lognpdf
manova1
mlecov
nancov
nansum
nbinrnd
ncfstat
ncx2cdf
nlintool
normlike
parallelcoords
pdist
poissrnd
prctile
randg
raylcdf
rcoplot
robustdemo
runstest
squareform
surfht
tiedrank
treetest
ttest2
unifcdf
var
wblinv
wishrnd
C:\Program Files\MATLAB\R2007a\toolbox
Stats dosyasını açalım.
Şimdi, corr (corr.m) dosyasını açalım.
Oldukça uzun bir Matlab programı. Ne yapıp yapmadığı konusunda yardım isteyelim:
Komut penceresinde: >> help corr
Bir uygulama yapalım.
Eğer yapmak istediğiniz analizler veya hesaplamalar ile ilgili bir fonksiyon Matlab içerisinde
hazır olarak bulunmuyor ise Matlabın gelişmiş kod yazma özelliğini kullanarak yapmak
istediğiniz analiz için kendi fonksiyon veya programınızı yazabilirsiniz.
Matlab’da programlama en genel olarak iki yolla yapılır:
- komut satırında (in-line) programlama
- m-dosyalarıyla (m-files) programlama
m-dosyalarının da iki türü vardır:
- Düzyazı (script) m-dosyaları
- Fonksiyon (function) m-dosyaları
m dosyaları oluşturabilmek için bir metin editörüne ihtiyaç vardır. Bu editör Matlab’da
Editor/Debugger ortamıdır
- Programlar (M-file → *.m)
- Grafik (Figure → *.fig)
GRAFĐKLER
Matlab, 2D ve 3D başta olmak üzere çok gelişmiş grafik araçları sunar:
Çizgi (line) grafikler (plot, plot3, polar)
Yüzey (surface) grafikler (surf, surfc)
Ağ (mesh) grafikler (mesh, meshc, meshgrid)
Contour grafikler (contour, contourc, contourf)
Çubuk (bar), pasta (pie) vb özel grafikler (bar, bar3, hist, rose, pie, pie3)
2D Veri Grafikleri
Standart normal dağılımın olasılık yoğunluk fonksiyonunun grafiğ.
x=-4:0.01:4;
plot(x,normpdf(x,0,1),'k')
% veya
fplot('normpdf(x,0,1)',[ -4,
% biçiminde de çizdirilebilir.
4])
Birden fazla grafiği (aynı x-ekseni baz olmak üzere) üst üste çizmek için
1.yol: plot(x,y1,x,y2,..x,yn)
2.yol: plot(x,y1), hold on, plot(x,y2,..x,yn).
>> t = 0:0.01:20;plot(t,sin(t),t,cos(t),t,sin(t)+cos(t))
1.5
1
0.5
0
-0.5
-1
-1.5
0
2
4
6
8
10
Çok Sayıda Grafik (Subplot)
Örnek: y=et,z=esint,w=yz grafiklerini alt alta çizelim.
subplot(3,1,1)
t = 0:0.01:50;
y = exp(t);
plot(t,y)
legend('e^{t+1}')
subplot(3,1,2)
z = sin(t);
plot(t,z)
legend('sin(t)')
subplot(3,1,3)
w = y.*z;
plot(t,w)
legend('e^{t+1}sin(t)')
12
14
16
18
20
ÜÇ BOYUTLU GRAFĐKLER
Matlab üç boyutlu (3D) grafik konusunda çok gelişmiş imkanlar sunar.
*3D çizgi grafikler - Üç boyutlu uzayda çizgi grafikleri çizer (plot3),
*3D ağ grafikler - Üç boyutlu uzayda tel çerçeveli yüzeyler çizer (mesh, meshc, meshz,
waterfall).
*3D yüzey grafikler (surf, shading, surfc, surfl, surfnorm).
*3D halka grafikler (contour3, contourf, shading, clabel).
*3D hacim grafikler (slice, isosurface, smooth3, isocaps, isonormals).
*3D özelleştirilmiş grafikler (ribbon, quiver, quiver3, fill3, stem3, sphere, cylinder).
*Serpilme grafiği (scatter3)
Örnekler:
% 3D Çizgi Grafiği:
X = [10 20 30 40];Y = [10 20 30 40];Z = [0 230 75 600];
plot3(X,Y,Z);
grid on;
xlabel('x-ekseni');
ylabel('y- ekseni');
zlabel('z- ekseni');
title('Üc boyutlu bir dogru');
% z=x2+y2 ile tanımlı 3D parabol grafiği:
figure
x = [-10 : 1 : 10];y = [-10 : 5 : 10];
[X, Y] = meshgrid(x,y);
Z = X.^2 + Y.^2; %üç boyutlu parabol
mesh(X,Y,Z);
xlabel('x-ekseni');ylabel('y- ekseni');zlabel('z- ekseni');
t = -2*pi:pi/100:2*pi;
[x,y,z] = cylinder(cos(t),20);
mesh(x,y,z)
axis off
Serpilme Grafiği
t = 0:pi/10:2*pi;
[X,Y,Z] = cylinder(2+cos(t));
surf(X,Y,Z)
ĐŞLEÇLER: Đşlem yapmayı sağlayan sembollerdir.
Aritmetik Đşleçler:
+
*
/
\
b
^ (üs alma, a ) : 2^3
‘ ‘(Tek tırnak arası) : ‘istatistik‘ (Metin girişlerinde kullanılır)
‘ : Transpoze
( ) : 2*(3-4) (Đşlem sırasını belirler)
( ) : sin(x)
[ ] : Dizi gösteriminde kullanılır.
= : x=3
==: x==K
<
Küçüktür
<=
Küçük eşittir
>
Büyüktür
>=
Büyük eşittir
==
Eşittir
~=
Eşit değildir
Mantıksal Đşleçler:
~
NOT (değil)
&
AND (ve)
|
OR (veya)
Sembolik Đşlemler
Matlab’de sembolik işlemler yapmak için sembolik değişkenler
>> syms a b x
komutu ile atanır.
Örnek:
∫ ( −2 x
5
− 4 x + 20)dx
» syms x
» int(-2*x^5-4*x+20)
ans =
-1/3*x^6-2*x^2+20*x
Örnek: x2-x-6=0
>> solve('x^2-x-6')
veya
>> syms x, solve(x^2-x-6)
ans =
[ -2]
[ 3]
Örnek: f(x)=5x3+ax2+bx -14
>> syms a b c x
>> f=5*x^3+a*x^2+b*x-14;
>> diff(f)
ans =
15*x^2+2*a*x+b
>> diff(f,x)
ans =
15*x^2+2*a*x+b
Örnek: Denklem sistemi.
>> [x,y] = solve('x^2 + x*y + y = 3','x^2 - 4*x + 3 = 0')
x=
[ 1]
[ 3]
y=
[ 1]
[ -3/2]
Çözüm kümesi={ (1,1) , (3,-3/2) }
Bazı Kullanım Alanları:
Matematiksel (nümerik ve sembolik) hesaplama işlemleri
Algoritma geliştirme ve kod yazma (programlama)
Lineer cebir, Fourier analizi,filtreleme,optimizasyon,sayısal integrasyon vb. konular.
2D ve 3D grafik çizimi
Modelleme ve simülasyon (benzetim)
Grafiksel arayüz oluşturma
Veri analizi