ρ ϕ ρ ϕ ρ ϕ ρ ϕ ρ ρ ϕ ρ ρ ρ ϕ ρ ϕ ρ ϕ ρ ϕ ρ ϕ ρ ρ ϕ ρ ϕ ρ ϕ ρ (ρ0
advertisement

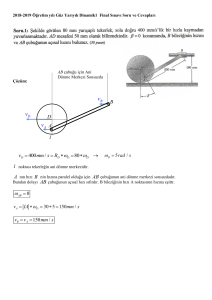
22.08.2011 MEKANİK FİNAL Soru 1. Bir parçacık F = a ρ sin ϕ ρˆ + b ρ cos ϕ φˆ (1.1) kuvveti altında hareket etmektedir. Bu kuvvetin korunumlu olması için a ve b katsayıları arasındaki ilişki ne olmalıdır. Buradan potansiyeli z bulunuz. Aşağıdaki şekli kullanabilirsiniz. Orijinden başlayarak (ρ0, ϕ0, z0) kadar integrasyonu alınır. (ρ0,ϕ0,z0) r C3 0 ρ0 (ρ0,0,0) C1 y ϕ0 ρ0 (ρ0,ϕ0,0) x C2 Cevap 1. Kuvvet silindirik koordinatlarda verilmiş ve bundan dolayı silindirik koordinatlarda çalışmamız daha pratik ve hızlı olacaktır. O halde silindirik koordinatlarda kuvvet bileşenleri Fρ = a ρ sin ϕ , Fϕ = bρ cos ϕ , Fz = 0 (1.2) ile verilir. Bu korunumlu kuvvet ise silindirik koordinatlarda kuvvetin rotasyonu sıfır olmalıdır. O halde (1.2) ile verilen kuvvetin rotasyonunu ⎛ 1 ∂Fz ∂Fϕ ∇×F = ⎜ − ⎝ ρ ∂ϕ ∂z ⎞ ⎛ ∂Fρ ∂Fz − ⎟ ρˆ + ⎜ ⎠ ⎝ ∂z ∂ρ ⎞ 1 ⎛ ∂ ( ρ Fϕ ) ∂Fρ − ⎟ φˆ + ⎜⎜ ρ ⎝ ∂ρ ∂ϕ ⎠ ⎞ ⎟ zˆ ⎟ ⎠ 2 ⎛ ∂ (bρ cos ϕ ) ⎞ ˆ ⎛ ∂ (a ρ sin ϕ ) ⎞ ˆ 1 ⎜⎛ ∂ ( bρ cos ϕ ) ∂ (a ρ sin ϕ ) ⎟⎞ = ⎜− − zˆ (1.3) ⎟ρ + ⎜ ⎟φ + ⎜ ⎟ ρ ∂z ∂z ∂ρ ∂ϕ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ = 0ρˆ + 0φˆ + 1 ρ ( 2bρ cos ϕ − a ρ cos ϕ ) zˆ = 0 ⇒ a = 2b ancak a = 2b koşuluyla bütün bileşenleri sıfır olur. Bu koşul altında korunumlu olduğundan dolayı o halde potansiyel enerjiyi bulalım. Bunun için şekilde verilen C1, C2 ve C3 ile isimlendirilmiş kesikli çizgili yolu orijinden başlayarak herhangi bir (ρ0, ϕ0, z0) noktasındaki potansiyel enerjiyi hesaplayalım: r r V (r ) = − ∫ F ⋅ dr = − ∫ ( Fρ ρˆ + Fϕ φˆ + Fz zˆ ) ⋅ ( d ρ ρˆ + ρ dϕ φˆ + dzzˆ ) rs rs ρ ϕ (1.4) z = − ∫ Fρ d ρ − ∫ Fϕ ρ dϕ − ∫ Fz dz ρs zs s ϕ C1 i. C2 C3 C1 yolu boyunca ϕ = 0 and z = 0 olduğundan Fρ = 0 olacak ve C1 integrasyonundan C1 = ρ0 ∫ Fρ d ρ = 0 (1.5) 0 ii. hiç bir katkı gelmeyecektir. C2 yolu boyunca ρ =ρ 0 and z = 0 olduğundan Fϕ = bρ 0 cos ϕ olacak ve C2 integrasyonundan C2 = ϕ0 ∫ Fϕ ρ dϕ = bρ ∫ cos ϕ dϕ = bρ 0 iii. ϕ0 2 0 2 0 ϕ (− sin ϕ ) 0 0 = −b ρ 02 sin ϕ0 (1.6) 0 katkısı gelecektir. C3 yolu boyunca ϕ =ϕ0 and ρ =ρ 0 ve Fz = 0 olduğundan C3 integrasyonu z0 C3 = ∫ Fz dz = 0 (1.7) 0 hiç bir katkı gelmeyecektir. Bulduğumuz bu sonuçları (1.4)'de yerine koyarsak ve en genel şekilde ifade etmek için (ρ0, ϕ0, z0) yerine (ρ, ϕ, z) konularak V (r ) = bρ 2 sin ϕ (1.8) potansiyeli bulunmuş olur. Soru 2. m kütleli bir parçacık şekilde gösterilen l uzunluğundaki sürtünmesiz bir tahta parçasının bir ucunda durmaktadır. Bu tahta parçacısının diğer ucu sabit kalmak koşulu ile kütlenin olduğu yerden teğet υ0 hızıyla kaldırılmaktadır. Sistemin hareketini Lagrange tekniği kullanarak hareket denklemini çıkartınız ve çözünüz. υ0 r υ0 θ l Çözüm 2. Parçacığın hareketi en güzel düzlem kutupsal koordinatlarda çözülerek elde edilir. Tahtanın dönme noktasını orijin kabul edersek şekilde gösterildiği gibi parçacığın konumu r ve tahtanın hareket doğrultusunda yapmış olduğu açıya θ dersek o zaman parçacığın Lagranjeni 1 (2.1) L = T − V = m r 2 + r 2θ 2 − mgr sin θ 2 elde edilir. Tahta υ0 hızıyla kaldırıldığından dolayı ( υ0 = θl ⇒ θ = ) υ0 ve θ= υ0 t l l olacaktır. O zaman Lagranjiyen υ 2r 2 ⎞ 1 ⎛ ⎛υ ⎞ L = T − V = m ⎜ r 2 + 0 2 ⎟ − mgr sin ⎜ 0 t ⎟ l ⎠ 2 ⎝ ⎝ l ⎠ olacaktır. O halde r için sistemin hareket denklemi d ∂L ∂L − =0 dt ∂r ∂r υ02 ⎛υ ⎞ mr − m 2 r + mg sin ⎜ 0 t ⎟ = 0 l ⎝ l ⎠ Soru 3. Kütlesi m ve açısal momentumu l olan bir cisim merkezcil bir kuvvet altında u = ρ −1 = a sin(nθ ) ile verilen yörüngede hareket etmektedir. Burada a ve n sabitlerdir. a. Merkezcil kuvveti bulunuz (ρ cinsinden). b. Etkin potansiyeli bulunuz (ρ cinsinden)? c. Sistemin toplam enerjisini bulunuz. (2.2) (2.3) (2.4) Çözüm 3. Parçacığın yörünge denklemi verilmektedir. O halde bunu merkezcik kuvvet altında elde edilen yörünge denkleminde yerine koyarsak d 2u m + u = − 2 2 F (u −1 ) 2 dθ lu N − n 2u l 2u 2 l 2 (1 − n 2 ) 3 u − n 2u + u ) = − ( m m l 2 (1 − n 2 ) 1 F (ρ ) = − m ρ3 elde edilir. Buradan potansiyel enerji ρ ρ l 2 (1 − n 2 ) 1 l 2 (1 − n 2 ) 1 ρ = − V ( ρ ) = − ∫ F ( ρ )d ρ = d ∫ ρ3 2m ρ 2 m ∞ ∞ elde edilir. Etkin potansiyel ise l2 l2 l 2 (1 − n 2 ) 1 l 2 n 2 1 Vetk = + V (ρ ) = − = 2m ρ 2 2m ρ 2 2m ρ 2 2m ρ 2 elde edilir. Kinetik enerji ise l d ρ du dθ nl = − ρ 2 an cos(nθ ) = − a cos(nθ ), ρ = 2 du dθ N dt m mρ N F (u −1 ) = − −ρ2 (3.1) (3.2) (3.3) θ = l mρ 2 θ (3.4) 1 1 nl nl 2 nl ⎛ 2 1 ⎞ mρ 2 = m 2 a 2 cos 2 (nθ ) = a (1 − sin 2 (nθ ) ) = ⎜a − 2 ⎟ ρ ⎠ 2 2 m 2m 2m ⎝ elde edilir. Sistemin toplam enerjisi (3.3) ve (3.4)'den n 2l 2 ⎛ 2 1 ⎞ n 2l 2 1 n 2l 2 a 2 = E = T + Vetk = ⎜⎜ a − 2 ⎟⎟ + 2m ⎝ ρ ⎠ 2m ρ 2 2m sabit bir enerji değeri bulunur. T= 2 2 2 2 2 2 (3.5)