Ders Adı
12.Sınıf – Mezun
LYS MATEMATİK
KONU ANLATIM FASİKÜLÜ
TÜREV KAF 01
Konu
Türeve Giriş
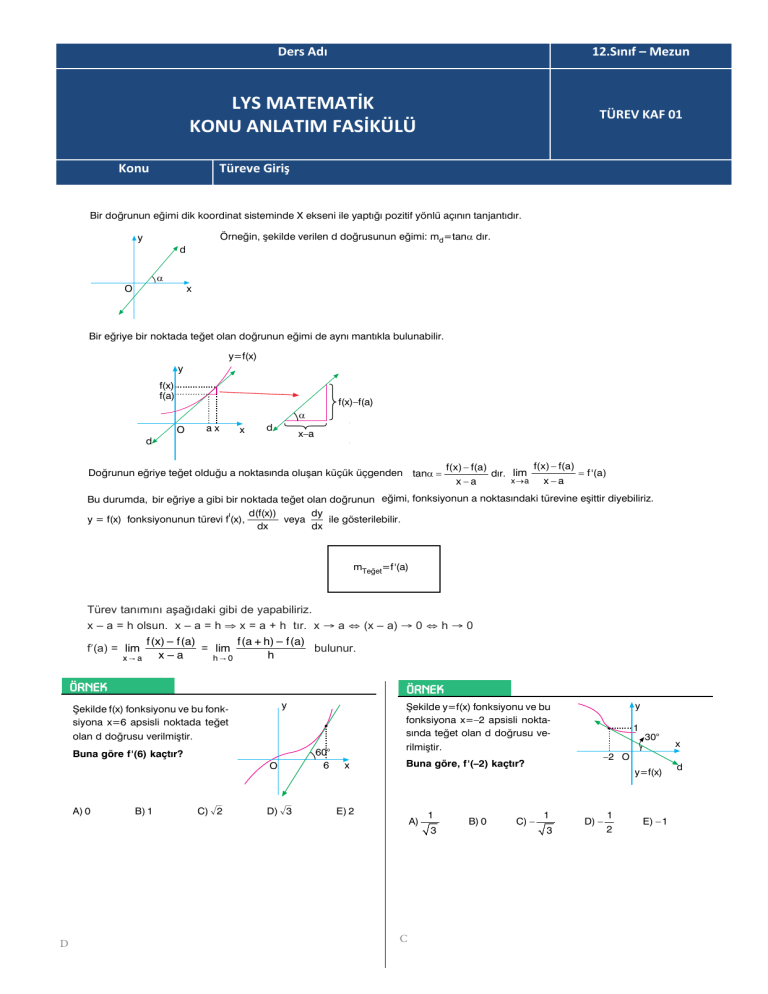
Bir doğrunun eğimi dik koordinat sisteminde X ekseni ile yaptığı pozitif yönlü açının tanjantıdır.
Örneğin, şekilde verilen d doğrusunun eğimi: md=tana dır.
Bir eğriye bir noktada teğet olan doğrunun eğimi de aynı mantıkla bulunabilir.
Doğrunun eğriye teğet olduğu a noktasında oluşan küçük üçgenden tana =
f(x) − f(a)
x−a
dır. lim
f(x) − f(a)
x →a
x−a
= f '(a)
Bu durumda, bir eğriye a gibi bir noktada teğet olan doğrunun eğimi, fonksiyonun a noktasındaki türevine eşittir diyebiliriz.
d(f(x))
dy
ı
veya
ile gösterilebilir.
y = f(x) fonksiyonunun türevi f (x),
dx
dx
mTeğet=f '(a)
Türev tanımını aşağıdaki gibi de yapabiliriz.
x – a = h olsun. x – a = h ⇒ x = a + h tır. x → a ⇔ (x – a) → 0 ⇔ h → 0
f (a + h) – f (a)
f (x) – f (a)
f′(a) = lim
= lim
bulunur.
h
x
–
a
x"a
h"0
ÖRNEK
ÖRNEK
Şekilde f(x) fonksiyonu ve bu fonksiyona x=6 apsisli noktada teğet
olan d doğrusu verilmiştir.
Buna göre f '(6) kaçtır?
A) 0
D
B) 1
C) ñ2
D) ñ3
Şekilde y=f(x) fonksiyonu ve bu
fonksiyona x=–2 apsisli noktasında teğet olan d doğrusu verilmiştir.
Buna göre, f '(–2) kaçtır?
E) 2
A)
C
1
3
B) 0
C) −
1
3
D) −
1
2
E) − 1
Türeve Giriş
LYS MATEMATİK
ÖRNEK
ÖRNEK
f(x) = 2x + 1
fý(5) in eþiti aþaðýdakilerden hangisidir?
f(x) – f(5)
f(x) + f(5)
B) lim
C) lim
x →0
x→ 0
x–5
x +5
f(x) – f(5)
f(x) + f(5)
D) lim
E) lim
x→5
x→ 5
x–5
x+5
f(x) – f(5)
A)
x–5
oldu¤una göre,
ri kaçt›r?
A) 2
lim
f(x) – f(1)
x–1
ifadesinin de¤e-
C) –1
D) 0
x→1
B) 1
E) –2
D
ÖRNEK
ÖRNEK
Aşağıdaki ifadelerin eşitlerini yazınız.
f(1 + h) – f(1)
=....................
h→0
h
lim
f(x) = 3x + 5
oldu¤una göre,
de¤eri kaçt›r?
A) 1
lim
x→1
f(x) – f(1)
x–1
f (x ) – f π
4
lim
x→π
x –π
4
4
lim h→ 0
B) 2
lim
h→0
f(2 + h) – f(2)
h
C) 3
D) 4
ifadesinin
E) 8
=....................
=....................
f(x + 2h) – f(x )
=....................
h
ÖRNEK
f(1 + 3h) – f(1)
=....................
lim h→0
h
f : R → R her noktada türevli bir fonksiyon ve
f'(1) = 3 oldu¤una göre,
f(3 + 2h) – f(3 – 3h)
lim
h→0
h
lim
h→0
f(1 + 3h) – f(1 – 2h)
h
lim
h→0
=....................
f(1 + 2h) – f(1 – 3h)
h
A) 15
B) 12
kaçt›r?
C) 9
D) 6
E) 3
(2006 - ÖSS 2)
=....................
A
Türeve Giriş
LYS MATEMATİK
ÖRNEK
Sağdan ve Soldan Türev
f(x) =
A ⊂ R ve f : A → R, y = f(x) fonksiyonu
a ∈ A da sürekli olmak üzere;
lim
®
x " a+
x 2 – 2 , x < 1 ise
olarak tan›mlan›yor. Buna göre, afla¤›dakilerden
hangisi yanl›flt›r?
sa, bu değere y = f(x) fonksiyonunun x = a daki
A) f'(1+) = 2
B) f'(1–) = 2
sağdan türevi denir ve f′(a+) ile gösterilir.
C) f'(1) = 2
D) lim f(x) = 2
lim
®
f (x) – f (a)
limitinin bir reel sayı değeri varx–a
2x – 3 , x ≥ 1 ise
x " a–
x→2
E) f fonksiyonu x = 1 de süreklidir.
f (x) – f (a)
limitinin bir reel sayı değeri varx–a
sa, bu değere y = f(x) fonksiyonunun x = a daki
soldan türevi denir ve f′(a–) ile gösterilir.
Sağdan ve soldan türevler var ve eşitse fonksiyonun o noktada türevi vardır.
+
D
–
f′(a ) = f′(a ) = f′(a) dır.
f′(a+) ≠ f′(a–) ise f′(a) yoktur.
A ⊂ R, f : A → R ve a ∈ A olmak üzere,
y = f(x) fonksiyonu x = a da türevli ise, bu noktada
ÖRNEK
süreklidir.
4x – 1 , x ≥ 1 ise
Bir başka ifadeyle, y = f(x) fonksiyonu x = a da
f(x) =
sürekli değilse, fonksiyonun bu noktada türevi yoktur.
2
2x + 1 , x < 1 ise
fonksiyonu için, f'(1) ifadesinin de¤eri kaçt›r?
A) 5
B) 4
C) 3
D) 2
E) Türev yoktur.
Bir noktada sürekli olan bir fonksiyon bu noktada
türevli olmayabilir. Fonksiyonun sürekli olduğu fakat
türevli olmadığı noktalara fonksiyonun kırılma noktaları adı verilir.
Türev - Süreklilik İlişkisi
B
ÖRNEK
f(x) = |x2 – 1|
fonksiyonu veriliyor. Buna göre, f'(1–) + f'(1+)
toplam› kaçt›r?
A) –2
C
B) –1
C) 0
D) 1
E) 2
Türeve Giriş
LYS MATEMATİK
ÖRNEK
f(x) =
x2 + 3
x2 – 1
fonksiyonunun türevinin olmadığı
kaç farklı noktası vardır?
ÖRNEK
y
a
b
c
d
e
x
f
2
y = f(x) fonksiyonunun grafi¤i verilmifltir.
Buna göre, afla¤›dakilerden hangisi do¤rudur?
A) f(x), x = a da türevli de¤ildir.
ÖRNEK
B) f(x), x = b de tan›ml› ve süreklidir.
f(x) = *
C) f(x), x = c de sürekli ve türevlidir.
D) f(x) in x = f de limiti yoktur.
E) f(x), x = e de sürekli ve türevlidir.
y
4
–2 –1
1 2
3
5
6
x
–1
(–4, 6] aral›¤›nda tan›ml› f fonksiyonunun grafi¤i verilmifltir.
Buna göre, x in –3, –2, –1, 0, 1, 2, 3, 4, 5 de¤erlerinin kaç›nda f nin türevi vard›r?
A) 0
B) 1
C) 2
x2 – 1 , x < 2
fonksiyonunun x0 = 2
apsisli noktasında türevi varsa kaçtır?
ÖRNEK
–4
4x + 1 , x ≥ 2
D) 3
E) 4
Türeve Giriş
LYS MATEMATİK
ÖRNEK
y
3
2
y = f(x)
1
0
2
3
4
5
6
8
x
Yukarıda grafiği verilen y = f(x) fonksiyonunun apsisi
verilen noktalarındaki türev-süreklilik ilişkisini inceleyiniz.
0 noktası için
L =....................
S =....................
T =....................
..........................................................................................
2 noktası için
L =....................
S =....................
T =....................
..........................................................................................
3 noktası için
L =....................
S =....................
T =....................
..........................................................................................
4 noktası için
L =....................
S =....................
T =....................
..........................................................................................
5 noktası için
L =....................
S =....................
T =....................
..........................................................................................
6 noktası için
L =....................
S =....................
T =....................
UYGULAMA
LYS MATEMATİK
ÖRNEK
ÖRNEK
y
Türevlenebilir bir f : R → R fonksiyonu için
f′(x) = 2x2 – 1 ve f(2) = 4 olduğuna göre,
1
f (x) – 4
limitinin değeri kaçtır?
x–2
lim
x"2
A) 3
B) 4
C) 5
y = f(x)
2
D) 6
0
E) 7
1
2
3
4
5
6
7
x
f : [ 0, 7 ] A [ 0, 2 ] fonksiyonunun grafiԫi yukarԩda
verilmiԭtir. f(x) fonksiyonu, ( 0, 7 ) aralԩԫԩnda
kaç noktada türevsizdir?
A) 2
ÖRNEK
C) 4
D) 5
E) 6
ÖRNEK
Gerçel say›lar kümesi üzerinde, tan›ml› ve türevlenebilir bir f fonksiyonu için,
f(x + y) = f(x) + f(y) + xy ,
oldu¤una göre, f'(1) kaçt›r?
A) 2
B) 3
B) 3
C) 4
lim
h→0
f(h)
=3
h
D) 5
E) 6
(2007 - ÖSS 2)
Z 2
] kx + 2x
]
f(x) = [ 3x + p
] 3
] x +t
\
fonksiyonunun x = 2
,
x > 2 ise
,
x = 2 ise
,
x < 2 ise
apsisli noktada türevi var-
sa, k.t – p kaçtԩr?
A) 5
B) 6
C) 7
D) 8
E) 10
ÖRNEK
y
y = f(x)
ÖRNEK
2
f (2 + 2h) – f (2 – 2h)
3h
ifadesininԭitie aԭaԫԩdakilerden hangisidir?
lim
0
h" 0
4
B) f ԩ c m
3
A) 0
2 ԩ
.f (2)
3
C)
E)
1 ԩ
.f (4)
3
4 ԩ
.f (2)
3
4
x
Yukarԩda grafiԫi verilen f(x) fonksiyonu için aԭaԫԩdakilerden hangisi yanlԩԭtԩr?
A) lim f(x) = 2
x"4
B) lim
f (x) – f (4)
= f ԩ(4)
x–4
C) lim
f (x) – f (4)
=0
x–4
x"4
x" 4–
D) lim f(x) = f(4)
x" 4 +
E) lim
x" 4 +
f (x) – f (4) 1
=
x–4
2
