Bir Fonksiyonun Dört Farklı Gösterimi Bir Fonksiyonun Dört Farklı

Bir Fonksiyonun Dört Farklı Gösterimi
Bir Fonksiyonun Dört Farklı Gösterimi
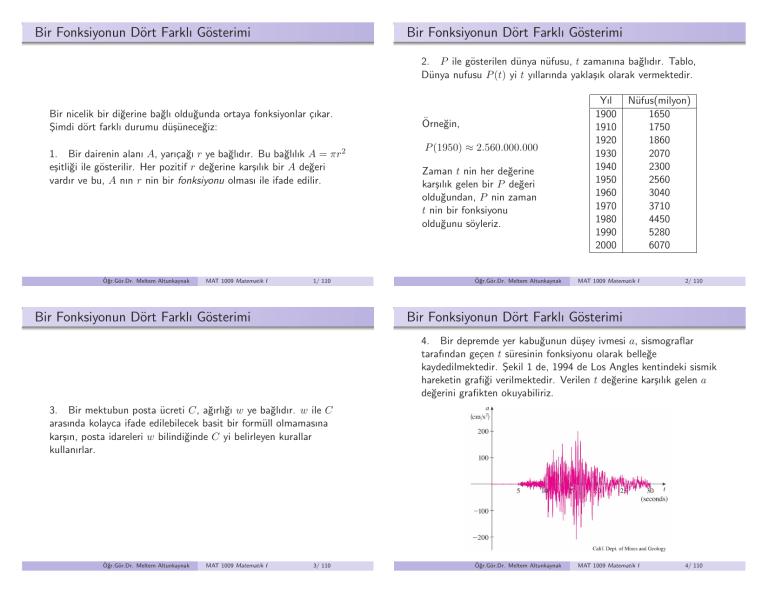
2. P ile gösterilen dünya nüfusu, t zamanına bağlıdır. Tablo,
Dünya nufusu P (t) yi t yıllarında yaklaşık olarak vermektedir.
Bir nicelik bir diğerine bağlı olduğunda ortaya fonksiyonlar çıkar.
Şimdi dört farklı durumu düşüneceğiz:
1. Bir dairenin alanı A, yarıçağı r ye bağlıdır. Bu bağlılık A = πr2
eşitliği ile gösterilir. Her pozitif r değerine karşılık bir A değeri
vardır ve bu, A nın r nin bir fonksiyonu olması ile ifade edilir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
1/ 110
Bir Fonksiyonun Dört Farklı Gösterimi
Örneğin,
P (1950) ≈ 2.560.000.000
Zaman t nin her değerine
karşılık gelen bir P değeri
olduğundan, P nin zaman
t nin bir fonksiyonu
olduğunu söyleriz.
Öğr.Gör.Dr. Meltem Altunkaynak
Yıl
1900
1910
1920
1930
1940
1950
1960
1970
1980
1990
2000
Nüfus(milyon)
1650
1750
1860
2070
2300
2560
3040
3710
4450
5280
6070
MAT 1009 Matematik I
2/ 110
Bir Fonksiyonun Dört Farklı Gösterimi
4. Bir depremde yer kabuğunun düşey ivmesi a, sismograflar
tarafından geçen t süresinin fonksiyonu olarak belleğe
kaydedilmektedir. Şekil 1 de, 1994 de Los Angles kentindeki sismik
hareketin grafiği verilmektedir. Verilen t değerine karşılık gelen a
değerini grafikten okuyabiliriz.
3. Bir mektubun posta ücreti C, ağırlığı w ye bağlıdır. w ile C
arasında kolayca ifade edilebilecek basit bir formüll olmamasına
karşın, posta idareleri w bilindiğinde C yi belirleyen kurallar
kullanırlar.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
3/ 110
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
Şekil
1: Northridge depreminde
düşey yer ivmeleri
4/ 110
Bir Fonksiyonun Dört Farklı Gösterimi
Tanım: Fonksiyon
Bir f fonksiyonu, bir A kümesinin her x öğesini, bir B kümesinin
tek bir f (x) öğesine taşıyan bir kuraldır.
Bu örneklerin tümü, verilen bir sayıya (r, t, w, veya t) karşılık diğer
bir sayıyı veren (A, P, C, veya a) bir kural belirler. Her bir
durumda ikinci sayı birincisinin fonksiyonudur.
Genellikle A ve B kümelerinin gerçel sayıların kümeleri olduğu
fonksiyonları düşüneceğiz.
A kümesine fonksiyonun tanım kümesi denir.
f (x) sayısına f fonksiyonunun x deki değeri denir.
x sayısı A kümesi içinde değişirken, f (x) in tüm olası değerlerinin
kümesine f nin görüntü kümesi denir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
5/ 110
Tanım: Fonksiyon
MAT 1009 Matematik I
6/ 110
Fonksiyon
Bir fonksiyonu en iyi anlamanın yolu grafiğidir. Tanım kümesi A
olan bir fonksiyonun grafiği
{(x, f (x))|x ∈ A}
ile betimlenen sıralı ikililer kümesidir.
f nin tanım kümesinin herhangi bir öğesini temsil eden sembole,
bağımsız değişken denir.
Görüntü kümesinin herhangi bir öğesini temsil eden sembole,
bağımlı değişken denir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
7/ 110
Başka bir deyişle, f
nin grafiği, x tanım
kümesinde ve
y = f (x) olmak
koşulu ile
düzlemdeki (x, y)
noktalarının
kümesidir.
Öğr.Gör.Dr. Meltem Altunkaynak
Şekil 2:
MAT 1009 Matematik I
8/ 110
Örnek
Fonksiyon
Grafik, f nin tanım ve görüntü kümelerini, sırası ile x− ve y−
ekseni üzerinde Şekil 3 deki gibi şekillendirmemize de yardımcı olur.
Örnek Üstü açık dikdörtgenler prizması şeklindeki bir kutunun
hacmi 10m3 tür. Tabanın uzun kenarı, kısa kenarının iki katıdır..
Tabanda kullanılacak malzemenin metrekaresi 10 YTL, yan
yüzlerde kullanılacak malzemenin metrekaresi 6 YTL ise, maliyet
fonksiyonunu kısa kenarın fonksiyonu olarak bulun.
Çözüm Şekil 4 da
kısa kenar w, uzun
kenar 2w ve
yükseklik h olarak
gösterilmiştir.
Şekil 4:
Şekil 3:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
9/ 110
Örnek...
MAT 1009 Matematik I
10/ 110
Örnek...
C yi w nin bir fonksiyonu olarak ifade edebilmek için h yi yok
etmemiz gerekir. Hacim 10m3 olduğu için
Taban alanı (2w) × w = 2w2
⇒
taban maliyeti 10(2w2 ) YTL.
İki yanyüzün alanı w × h, ikisinin alanı ise 2w × h dir. Buradan
yanyüzlerin alanı 2(wh) + 2(2wh) olur. Dolayısıyla yanyüzlerin
maliyeti 6 × [2(wh) + 2(2wh)] dir.
Toplam maliyet ise
C = 10(2w2 ) + 6[2(wh) + 2(2wh)] = 20w2 + 36wh
olur.
w × (2w) × h = 10
ve dolayısıyla
5
10
= 2
2
2w
w
dir. Bunu C nin ifadesinde yerine koyarak
180
5
2
C = 20w + 36w
= 20w2 +
2
w
w
h=
elde ederiz.
180
,
w>0
w
denklemi, C yi w nin fonksiyonu olarak ifade eder.
C(w) = 20w2 +
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
11/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
12/ 110
Fonksiyon
Fonksiyon
Düşey doğru ölçütü xy− düzlemindeki bir eğrinin x in bir
fonksiyonunun grafiği olması için gerekli ve yeterli koşul, her düşey
doğrunun bu eğriyi en fazla bir noktada kesmesidir.
Bir fonksiyonun grafiği xy− düzleminde bir eğridir. Bu durumda
akla bir soru geliyor: xy−düzlemindeki hangi eğriler bir
fonksiyonun grafiğidir?
Şekil 5: Düşey Doğru Ölçütü
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
13/ 110
Fonksiyonlar - Parçalı tanımlı fonksiyon
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
14/ 110
Fonksiyonlar - Parçalı tanımlı fonksiyon
Tanım kümesinin farklı parçalarında farklı biçimde tanımlanmış
fonksiyona parçalı fonksiyon denir.
1 − x, x ≤ 1
f (x) =
x2 ,
x>1
Parçalı tanımlı fonksiyonlara vereceğimiz bir sonraki örnek mutlak
değer fonksiyonudur.
x ,x ≥ 0
|x| =
−x , x < 0
x ≤ 1 iken f (x) in değeri 1 − x, x > 1 iken f (x) in değeri x2 dir.
Şekil 6:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
15/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
16/ 110
Fonksiyonlar - Simetrik fonksiyon
Fonksiyonlar - Simetrik fonksiyon
Bu fonksiyonların önemi, grafiklerinin y− eksenine göre simetrik
olmasıdır(Şekil 7). Yalnızca x ≥ 0 için grafik çizildiğinde, tüm
grafik y− eksenine göre simetri alınarak bulunur.
Tanım kümesindeki her x için f (−x) = f (x) koşulunu sağlayan f
fonksiyonuna çift fonksiyon denir.
Örneğin f (x) = x2 fonksiyonu için
f (−x) = (−x)2 = x2 = f (x)
sağlandığından f çifttir.
Şekil 7:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
17/ 110
Fonksiyonlar - Simetrik fonksiyon
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
18/ 110
Fonksiyonlar - Simetrik fonksiyon
Tek fonksiyonların grafikleri başlangıç noktasına göre
simetriktir.(Şekil 8).
Tanım kümesindeki her x için f (−x) = −f (x) koşulunu sağlayan f
fonksiyonuna tek fonksiyon denir.
Örneğin f (x) = x3 fonksiyonu tektir çünkü
f (−x) = (−x)3 = −x3 = −f (x)
dir.
Şekil 8:
Eğer x ≥ 0 değerleri için grafik biliniyorsa, tüm grafik eldeki
grafiğin başlangıç noktaı etrafında 180◦ döndürülmesiyle elde edilir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
19/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
20/ 110
Fonksiyonlar - Artan ve Azalan Fonksiyonlar
Fonksiyonlar - Artan ve Azalan Fonksiyonlar
Şekil 9:
Şekil 9 daki grafik A dan B ye kadar yükselmekte, B den C ye
kadar düşmekte ve C den D ye kadar tekrar yükselmektedir. f
fonksiyonu [a, b] aralığında artan, [b, c] aralığında azalan, [c, d]
aralığında ise yine artandır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
21/ 110
Fonksiyonlar - Artan ve Azalan Fonksiyonlar
I aralığındaki her x1 < x2 için f (x1 ) > f (x2 ) ise, f fonksiyonu I
aralığında azalandır denir.
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
22/ 110
Fonksiyonlar - Periyodik Fonksiyonlar
I aralığındaki her x1 < x2 için f (x1 ) < f (x2 ) ise, f fonksiyonu I
aralığında artandır denir.
Öğr.Gör.Dr. Meltem Altunkaynak
x1 ve x2 noktaları a ve b arasında, x1 < x2 koşulunu sağlayan
herhangi iki nokta ise, f (x1 ) < f (x2 ) olduğuna dikkat ediniz. Bu
özelliği artan fonksiyonun tanımı için kullanacağız.
23/ 110
Her bir x değeri için, p > 0 iken
f (x + p) = f (x)
eşitliğini sağlayan fonksiyonlara p periyoduna sahip periyodik
fonksiyon denir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
24/ 110
Fonksiyonlar - Polinomlar
Fonksiyonlar - Polinomlar
n bir tamsayı, a0 , a1 , a2 , . . . , an sabit gerçel sayılar olmak üzere
P (x) = an xn + an−1 xn−1 + . . . + a2 x2 + a1 x + a0
Örneğin,
√
2
P (x) = 2x6 − x4 + x3 + 2
5
derecesi 6 olan bir polinomdur.
şeklindeki fonksiyonlara polinom denir.
Her polinomun tanım kümesi R = (−∞, ∞) kümesidir.
Derecesi 1 olan polinom P (x) = mx + b biçiminde olacağından,
doğrusal bir fonksiyondur.
a0 , a1 , a2 , . . . , an sayılarına polinomun katsayıları denir. Eğer ilk
katsayı an 6= 0 ise, n sayısına polinomun derecesi denir.
Derecesi 2 olan bir polinom P (x) = ax2 + bx + c biçimindedir ve
kuadratik fonksiyon (veya ikinci dereceden polinom) adını taşır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
25/ 110
Fonksiyonlar - Polinomlar
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
26/ 110
Fonksiyonlar - Polinomlar
İkinci dereceden polinomların grafiği parabol olur ve grafikleri, bir
sonraki bölümde göreceğimiz gibi y = ax2 parabolünün
kaydırılması ile elde edilir. a > 0 ise, parabolun ağzı yukarıya,
a < 0 ise aşağıya doğru açıktır (Şekil 10).
Derecesi 3 olan bir polinom
ax3 + bx2 + cx + d
biçimindedir ve kübik fonksiyon adını taşır.
Şekil 10: y = x2 + x + 1
Öğr.Gör.Dr. Meltem Altunkaynak
y = −2x2 + 3x + 1
MAT 1009 Matematik I
27/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
28/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
Fonksiyonlar - Kuvvet Fonksiyonları
n pozitif bir tamsayı olmak üzere, a = n ise
n = 1, 2, 3, 4 ve 5 olduğu f (x) = xn fonksiyonlarının grafikleri
aşağıdaki grafiklerde görülmektedir. (Bunlar yalnızca bir terimi
olan polinomlardır.)
a sabit bir sayı olmak üzere,
f (x) = xa
biçimindeki fonksiyonlara kuvvet fonksiyonları denir.
Bazı özel durumları düşünelim:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
29/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
MAT 1009 Matematik I
MAT 1009 Matematik I
30/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
n pozitif bir tamsayı olmak üzere, a = n ise
n = 1, 2, 3, 4 ve 5 olduğu f (x) = xn fonksiyonlarının grafikleri
aşağıdaki grafiklerde görülmektedir. (Bunlar yalnızca bir terimi
olan polinomlardır.)
Öğr.Gör.Dr. Meltem Altunkaynak
Öğr.Gör.Dr. Meltem Altunkaynak
30/ 110
n pozitif bir tamsayı olmak üzere, a = n ise
n = 1, 2, 3, 4 ve 5 olduğu f (x) = xn fonksiyonlarının grafikleri
aşağıdaki grafiklerde görülmektedir. (Bunlar yalnızca bir terimi
olan polinomlardır.)
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
30/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
Fonksiyonlar - Kuvvet Fonksiyonları
n pozitif bir tamsayı olmak üzere, a =
Aşağıdaki şekilden görüleceği gibi n artarken f (x) = xn , 0
yakınında düzleşmekte, |x| ≥ 1 için dikleşmektedir.
f (x) = x1/n =
√
n
1
n
ise
x fonksiyonuna kök fonksiyonu denir.
√
n = 2 ise, f (x) = x, tanım kümesi [0, ∞), grafiği ise x = y 2
parabolünün üst kolu olan kare-kök fonksiyonudur.
n tamsayısının çift olması
durumunda, y = x1/n
fonksiyonunun grafiği
√
y = x fonksiyonunun
grafiğine benzer.
(x küçükse, x2 daha küçük, x3 daha da küçük, x4 ondan da küçük,
v.b. olacaktır.)
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
31/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
MAT 1009 Matematik I
32/ 110
Fonksiyonlar - Kuvvet Fonksiyonları
√
n = 3 durumunda f (x) = 3 x, tanım kümesi R olan
(her gerçel sayının küp-kökü vardır) küp-kök fonksiyonudur ve
grafiği aşağıda verilmiştir.
a = −1 ise
Şekil de, f (x) = x−1 = 1/x in grafiği verilmiştir.
n tek ise, (n > 3)
√
y = n x nin grafiği
√
y = 3 x fonksiyonunkine
benzer.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
33/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
34/ 110
Fonksiyonlar - Rasyonel Fonksiyonlar
Fonksiyonlar - Rasyonel Fonksiyonlar
P ve Q gibi iki polinomun oranı olarak ifade edilebilen
f (x) =
P (x)
Q(x)
f (x) =
f fonksiyonuna rasyonel (kesirli) fonksiyon denir.
2x4 − x2 + 1
x2 − 4
fonksiyonu da tanım kümesi {x|x 6= ±2} olan olan bir rasyonel
fonksiyondur.
Tanım kümesi: Q(x) 6= 0 olan tüm x sayılarıdır.
Tanım kümesi {x|x 6= 0} olan f (x) = 1/x fonksiyonu da rasyonel
bir fonksiyondur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
35/ 110
Fonksiyonlar - Cebirsel Fonksiyonlar
p
x2 + 1
g(x) =
MAT 1009 Matematik I
36/ 110
Fonksiyonlar - Trigonometrik Fonksiyonlar
Polinomlardan(toplama, çıkarma, çarpma, bölme ve kök alma gibi)
cebirsel işlemler ile elde edilebilen f fonksiyonuna cebirsel fonksiyon
denir. Rasyonel fonksiyonlar cebirsel fonksiyonlardır.
f (x) =
Öğr.Gör.Dr. Meltem Altunkaynak
Kalkülüste açı birimi olarak (aksi belirtilmediği sürece) radyan
kullanılır. Örneğin, f (x) = sin x ile radyan ölçümü x olan açının
sinüsünü anlarız. Dolayısı ile, sinüs ve kosinüs fonksiyonlarının
grafikleri, şekil de gösterildiği gibidir.
√
x4 − 16x2
√ + (x − 2) 3 x + 1
x+ x
fonksiyonları da cebirsel fonksiyonlardır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
37/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
38/ 110
Fonksiyonlar - Trigonometrik Fonksiyonlar
Fonksiyonlar - Trigonometrik Fonksiyonlar
Kalkülüste açı birimi olarak (aksi belirtilmediği sürece) radyan
kullanılır. Örneğin, f (x) = sin x ile radyan ölçümü x olan açının
sinüsünü anlarız. Dolayısı ile, sinüs ve kosinüs fonksiyonlarının
grafikleri, şekil de gösterildiği gibidir.
Sinüs ve kosinüs fonksiyonlarının tanım kümesi (−∞, ∞), görüntü
kümesi [−1, 1] kapalı aralığıdır. Bu nedenle her x için
−1 ≤ sin x ≤ 1
− 1 ≤ cos x ≤ 1
ya da mutlak değer gösterimi ile
| sin x| ≤ 1
| cos x| ≤ 1
olur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
38/ 110
Fonksiyonlar - Trigonometrik Fonksiyonlar
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
39/ 110
Fonksiyonlar - Trigonometrik Fonksiyonlar
Tanjant fonksiyonunun sinüs ve kosinüs fonksiyonalrı ile ilişkisi,
Sinüs fonksiyonunu sıfırları π nin tamsayı katlarıdır; başka bir
değişle n tamsayı olmak üzere,
sin x
cos x
denklemleriyle verilir. Grafiği aşağıda da verilmiştir.
tan x =
x = nπ için sin x = 0 dır.
Sinüs ve kosinüs fonksiyonlarının en önemli özelliği periyodik
olmaları ve periyodlarının 2π olmasıdır. Bu, x in tüm değerleri için
sin(x + 2π) = sin x cos(x + 2π) = cos x
olması demektir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
40/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
41/ 110
Fonksiyonlar - Trigonometrik Fonksiyonlar
Fonksiyonlar - Üstel Fonksiyonlar
Bu tür fonksiyonlar, taban a nın pozitif bir sabit olduğu
f (x) = ax
x = ±π/2, ±3π/2, . . . değerleri için cos x = 0 olduğundan, bu
değerlerde tanımlı değildir.
biçimindeki fonksiyonlardır. Her iki durumda da tanım kümesi
(−∞, ∞) ve görüntü kümesi (0, ∞) dur.
Görüntü kümesi (−∞, ∞) aralığıdır.
Tanjant fonksiyonu periyodiktir ve periyodu π dir:
tan(x + π) = tan x.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
42/ 110
Fonksiyonlar - Üstel Fonksiyonlar
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
43/ 110
Fonksiyonlar - Üstel Fonksiyonlar
Üstel fonksiyonların en çok kullanılanı ex (doğal üstel fonksiyon)
fonksiyonudur. Buradaki e sayısı üstel fonksiyonun y− eksenini
eğimi 1 olacak şekilde kesmesini saylayan sayıdır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
44/ 110
e sayısı irrasyonel bir sayıdır ve e sayısının ilk 5 basamağı
e ≈ 2.71828 dir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
45/ 110
Örnek
Fonksiyonlar - Cebirsel Olmayan Fonksiyonlar
ÖRNEK: Aşağıdaki fonksiyonların türlerini belirleyiniz.
Transandantal (aşkın) fonksiyonlar olarak da bilinen bu tür
fonksiyonlar trigonometrik, üstel ve logaritma fonksiyonlarını
içerdikleri gibi, hiç bir ad verilmemiş diğer pek çok fonksiyonu da
içerirler.
(a)
f (x) = 5x
(c)
h(x) =
1+x
√
1− x
(b)
g(x) = x5
(d)
u(t) = 1 − t + 5t4
ÇÖZÜM:
(a) f (x) = 5x fonksiyonu üstel bir fonksiyondur. (Kuvveti x dir.)
(b) g(x) = x5 fonksiyonu bir kuvvet fonksiyonudur. (Taban x
dir.) aynı zamanda derecesi 5 olan bir polinomdur.
1+x
√ cebirsel bir fonksiyondur.
(c) h(x) =
1− x
(d) u(t) = 1 − t + 5t4 derecesi 4 olan bir polinomdur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
46/ 110
Eski Fonksiyonlardan Yenilerini Elde Etmek
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
47/ 110
Fonksiyonların Dönüşümleri
Bu bölümde, önceki bölümde öğrendiğimiz temel fonksiyonlardan
başlayacağız ve grafiklerini kaydırarak, gererek ve yansıtarak yeni
fonksiyonlar elde edeceğiz. Ayrıca, bir fonksiyon çiftinin standart
aritmetik işlemler ve bileşkeyle nasıl birleştirildiğini göstereceğiz.
Bir fonksiyonun grafiğine dönüşümler uygulayarak yeni fonksiyonlar
elde edebiliriz.
Bu fikirler bize bir çok fonksiyonun grafiğini hızlıca çizebilme
yeteneğini kazandıracaktır.
Aynı zamanda, verilen grafiklerin denklemlerini bulabileceğiz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
48/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
49/ 110
Fonksiyonların Dönüşümleri
Fonksiyonların Dönüşümleri
c > 0 olmak üzere
Önce ötelemeleri düşünelim.
Eğer c pozitif bir sayı ise, y = f (x) + c fonksiyonunun grafiği
y = f (x) fonksiyonunun grafiğinin yukarı doğru c birim
kaydırılması ile elde edilir (bunun nedeni tüm y-koordinatlarının c
kadar arttırılmasıdır).
g(x) = f (x − c) ile tanımlanan g fonksiyonunun x sayısındaki
değeri, f nin x − c sayısındaki değeridir (başka bir deyişle, x in c
birim solundaki değer). Bu nedenle, y = f (x − c) fonksiyonunun
grafiği, y = f (x) grafiğinin c birim sağa kaydırılmış halidir
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
50/ 110
Fonksiyonların Dönüşümleri
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
51/ 110
Fonksiyonların Dönüşümleri
Yatay ve düşey kaydırmalar c > 0 olsun.
y = f (x) + c nin grafiğini elde etmek için,
y = f (x) grafiğini yukarı doğru c birim kaydırınız.
y = f (x) − c nin grafiğini elde etmek için,
y = f (x) grafiğini aşağıya doğru c birim kaydırınız.
y = f (x − c) nin grafiğini elde etmek için,
y = f (x) grafiğini sağa doğru c birim kaydırınız.
Şimdi germe ve yansıma dönüşümlerini ele alalım.
c > 1 ise, y = cf (x) fonksiyonunun grafiği, y = f (x)
fonksiyonunun grafiğinin düşey doğrultuda c kadar gerilmesi ile elde
edilir (çünkü her y-koordinatı aynı c sayısı ile çarpılmıştır).
y = −f (x) fonksiyonun grafiği, y = f (x) grafiğinin x− eksenine
göre yansımasıdır, çünkü (x, y) noktası (x, −y) noktası ile yer
değiştirmektedir.
y = f (x + c) nin grafiğini elde etmek için,
y = f (x) grafiğini sola doğru c birim kaydırınız.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
52/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
53/ 110
Fonksiyonların Dönüşümleri
Fonksiyonların Dönüşümleri
c > 1 ve c 6= 0 olmak üzere
Yatay ve düşey germe ve yansıma
c > 1 olsun.
y = cf (x) in grafiğini elde etmek için,
y = f (x) in grafiğini düşey olarak c kadar geriniz.
y = (1/c)f (x) in grafiğini elde etmek için,
y = f (x) in grafiğini düşey olarak c kadar büzünüz.
y = f (cx) in grafiğini elde etmek için,
y = f (x) in grafiğini yatay olarak c kadar büzünüz.
y = f (x/c) in grafiğini elde etmek için,
y = f (x) in grafiğini yatay olarak c kadar geriniz.
y = −f (x) in grafiğini elde etmek için,
y = f (x) in grafiğinin x− ekseninde yansımasını alınız.
y = f (−x) in grafiğini elde etmek için,
y = f (x) in grafiğinin y− ekseninde yansımasını alınız.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
54/ 110
Örnek
MAT 1009 Matematik I
55/ 110
Örnek...
√
Örnek : Verilen y√= x in grafiğine dönüşümler uygulayarak
√
√
√
√
y = x − 2, y = x − 2, y = − x, y = 2 x ve y = −x
fonksiyonlarının grafiklerini çiziniz.
√
Çözüm : y = x in grafiği:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
56/ 110
2 birim aşağı kaydırarak y =
√
x − 2 fonksiyonunun grafiği:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
57/ 110
Örnek...
Örnek...
2 birim sağa kaydırarak y =
√
√
x− ekseninde yansımasını alarak y = − x in grafiği:
x − 2 fonksiyonun grafiği:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
58/ 110
Örnek...
MAT 1009 Matematik I
59/ 110
Örnek...
√
düşey yönde 2 birim gererek y = 2 x in grafiği:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
y− ekseninde yansıma alarak y =
60/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
√
−x in grafiği:
MAT 1009 Matematik I
61/ 110
Örnek
Örnek
Örnek : f (x) = x2 + 6x + 10 fonksiyonunun grafiğini çiziniz.
Çözüm: Tam kareye tamamlayarak, grafiğin denklemini
y = x2 + 6x + 10 = (x + 3)2 + 1
olarak yazarız. İstenilen grafiği, y = x2 parabolünü önce 3 birim
sola, sonra 1 birim yukarıya kaydırarak buluruz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
62/ 110
Fonksiyonların Birleşimleri
Örnek : y = |x2 − 1| fonksiyonunun garfiğini çiziniz.
Çözüm: Önce y = x2 − 1 parabolünü çizeriz. Bu, y = x2
parabolünün 1 birim aşağıya kaydırılmasıyla elde edilir.
−1 < x < 1 iken x2 − 1 parabolü x-ekseninin altında kaldığından,
y = |x2 − 1| in grafiğini, bu kısmın grafiğini x− eksenine göre
yansıtarak buluruz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
63/ 110
Fonksiyonların Birleşimleri
f + g toplamını,
f ve g gibi iki fonksiyon, sayıların toplanması, çıkarılması,
çarpılması ve bölünmesine benzer şekilde birleştirilerek, f + g,
f − g, f g ve f /g gibi yeni fonksiyonlar elde edilebilir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
64/ 110
(f + g)(x) = f (x) + g(x)
(1)
ile tanımlarsak, denklem 1 in sağ tarafı ancak f (x) ve g(x) in her
ikisininde tanımlı olduğu, diğer bir deyişle, x in hem f nin hem de
g nin tanım kümesinde olduğu zaman anlamlıdır. f nin tanım
kümesi A, g nin tanım kümesi B ise, f + g fonksiyonunun tanım
kümesi, bu iki tanım kümesinin kesişimi A ∩ B dir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
65/ 110
Örnek
Fonksiyonların cebiri
f ve g, tanım kümeleri A ve B olan fonksiyonlar olsun.
f + g, f − g, f g, ve f /g fonksiyonları aşağıdaki gibi tanımlanır.
(f + g)(x)
= f (x) + g(x)
tanım kümesi = A ∩ B
(f − g)(x)
= f (x) − g(x)
tanım kümesi = A ∩ B
(f g)(x)
= f (x)g(x)
tanım kümesi = A ∩ B
(f /g)(x)
= f (x)/g(x)
tanım kümesi = {x ∈ A ∩ B : g(x) 6= 0}
√
√
Örnek : f (x) = x, g(x) = 4 − x2 ise, f + g, f − g, f g, ve
f /g fonksiyonlarını bulunuz.
√
Çözüm : f (x) = x fonksiyonunun tanım kümesi [0, ∞) dur.
√
g(x) = 4 − x2 fonksiyonunun tanım kümesi, 4 − x2 ≥ 0, yani
x2 ≤ 4 eşitsizliğini sağlayan x değerlerinden oluşur.
Her iki tarafın kare kökünü alırsak, |x| ≤ 2, veya −2 ≤ x ≤ 2 elde
ederiz.
Dolayısıyla, g fonksiyonunun tanım kümesi [−2, 2] aralığıdır.
f ve g nin tanım kümelerinin kesişimi
[0, ∞) ∩ [−2, 2] = [0, 2]
kümesidir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
66/ 110
Örnek...
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
67/ 110
Fonksiyonların Bileşkesi
Böylece tanımlardan,
(f + g)(x)
(f − g)(x)
(f
g)(x)
f
(x)
g
√
√
= x + √4 − x 2
√
− 4 − x2 √
= x√
√
= 4x − x3
= x√ 4 − x2 r
x
x
=√
=
4 − x2
4 − x2
0≤x≤2
0≤x≤2
0≤x≤2
0≤x<2
Verilen f ve g fonksiyonları için f ◦ g bileşke fonksiyonu (ya da f
ve g nin bileşkesi),
(f ◦ g)(x) = f (g(x))
olarak tanımlanır.
buluruz. f /g nin tanım kümesinde g(x) = 0 veren x = ±2
noktalarının olmaması gerektiğinden, f /g nin tanım kümesi [0,2)
aralığıdır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
68/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
69/ 110
Fonksiyonların Bileşkesi
Fonksiyonların Bileşkesi
f ◦ g fonksiyonunu anlamanın en iyi yolu Şekil 11 deki gibi ok
gösterimidir.
f ◦ g fonksiyonunun tanım kümesi, g nin tanım kümesindeki, g nin
görüntüsü f nin tanım kümesinde olan x lerden oluşur.
Başka bir deyişle, (f ◦ g)(x), hem g(x) hem de f (g(x)) tanımlı
olduğu zaman tanımlıdır.
Şekil 11:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
70/ 110
Örnek
MAT 1009 Matematik I
71/ 110
Örnek
Örnek : f (x) = x2 ve g(x) = x − 3 ise, f ◦ g ve g ◦ f bileşke
fonksiyonlarını bulunuz.
Çözüm:
Çözüm:
(f ◦ g)(x) = f (g(x)) = f (x − 3) = (x − 3)2
(a)
(g ◦ f )(x) = g(f (x)) = g(x2 ) = x2 − 3
Not : Örnekte görüldüğü gibi, genelde f ◦ g 6= g ◦ f dir. f ◦ g,
önce g sonra f nin uygulanması ile bulunur. Örnekteki f ◦ g
fonksiyonu, önce 3 çıkartan sonra da kare alan fonksiyon iken, g ◦ f
önce kare alan sonra 3 çıkartan fonksiyondur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
√
√
Örnek : f (x) = x ve g(x) = 2 − x ise aşağıdaki fonksiyonları
ve tanım kümelerini bulunuz.
(a) f ◦ g (b) g ◦ f (c) f ◦ f (d) g ◦ g
72/ 110
p√
√
√
(f ◦ g)(x) = f (g(x)) = f ( 2 − x) =
2−x= 42−x
f ◦ g fonksiyonunun tanım kümesi
{x|2 − x ≥ 0} = {x|x ≤ 2} = (−∞, 2]
dir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
73/ 110
Örnek...
Örnek...
p
√
√
(b)
(g ◦ f )(x) = g(f (x)) = g( x) = 2 − x
√
x fonksiyonun tanımlı olması için x ≥ 0 olmalıdır.
p
√
√
2 − x fonksiyonunun tanımlı olması için 2 − x ≥ 0 olmalıdır.
√
Bu, x ≤ 2 veya x ≤ 4 olmasını gerektirdiğinden, 0 ≤ x ≤ 4 olur.
(c)
p√
√
√
(f ◦ f )(x) = f (f (x)) = f ( x) =
x= 4x
f ◦ f fonksiyonunun tanım kümesi [0, ∞) aralığıdır.
Buradan g ◦ f fonksiyonunun tanım kümesi olarak [0, 4] bulunur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Örnek...
(d)
Öğr.Gör.Dr. Meltem Altunkaynak
74/ 110
MAT 1009 Matematik I
75/ 110
Örnek
p
√
√
(g ◦ g)(x) = g(g(x)) = g( 2 − x) = 2 − 2 − x
Bu ifadenin
tanımlı olması için 2 − x ≥ 0 ya da x ≤ 2 ve
√
2 − 2 − x ≥ 0 olmalıdır.
√
Son eşitsizlik 2 − x ≤ 2 ya da 2 − x ≤ 4 olmasına denktir.
Bu da −2 ≤ x ≤ 2 demek olduğundan, g ◦ g nin tanım kümesi
[−2, 2] kapalı aralığıdır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
76/ 110
Örnek : Verilen F (x) = cos2 (x + 9) için, F = f ◦ g ◦ h olacak
biçimde f , g ve h fonksiyonlarını bulunuz.
Çözüm: F (x) = [cos(x + 9)]2 olduğundan F fonksiyonu önce 9 ile
toplama, sonra toplamın kosinüsünü alma ve en sonunda da kare
alma demektir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
77/ 110
Örnek...
Ters Fonksiyonlar ve Logaritmalar
Böylece
h(x) = x + 9
g(x) = cos x
f (x) = x2
Aynı değeri iki kez almayan bir f fonksiyonuna, başka bir deyişle
olarak alırsak,
x1 6= x2 için f (x1 ) 6= f (x2 )
(f ◦ g ◦ h)(x) = f (g(h(x))) = f (g(x + 9)) =
koşuluna sağlayan bir fonksiyona, bire-bir fonksiyon denir.
f (cos(x + 9)) = [cos(x + 9)]2 = F (x)
elde ederiz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
78/ 110
Ters Fonksiyonlar ve Logaritmalar
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
79/ 110
Ters Fonksiyonlar ve Logaritmalar
Şekil 12 de görüldüğü gibi yatay bir doğru f nin grafiğini birden
fazla noktada kesiyorsa, f (x1 ) = f (x2 ) olan farklı x1 ve x2
olacağından f fonksiyonu bire-bir değildir.
Bu nedenle, bir fonksiyonun bire-bir olması için aşağıdaki
geometrik ölçütü verebiliriz.
Yatay Doğru Ölçütü Bir fonksiyonun bire-bir olması için gerek ve
yeter koşul, hiç bir yatay doğrunun grafiği bir kezden fazla
kesmemesidir.
Şekil 12:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
80/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
81/ 110
Ters Fonksiyonlar ve Logaritmalar
Ters Fonksiyonlar ve Logaritmalar
f , tanım kümesi A, görüntü kümesi B olan bire-bir bir fonksiyon
olsun.
f −1 in tanım kümesi = f nin görüntü kümesi
f −1 in görüntü kümesi = f nin tanım kümesi.
f fonksiyonunun tersi, f −1 , tanım kümesi B, görüntü kümesi A
olan ve B kümesindeki her y için
f −1 (y) = x ⇔ f (x) = y
ile tanımlanan fonksiyondur.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
82/ 110
Ters Fonksiyonlar ve Logaritmalar
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
83/ 110
Ters Fonksiyonlar ve Logaritmalar
Geleneksel olarak x ile bağımsız değişkeni gösterdiğimizden, eğer
f −1 ile çalışıyorsak tanımda x ve y nin yerlerini değiştirip
Örneğin, f (x) = x3 fonksiyonun tersi f −1 (x) = x1/3
fonksiyonudur.
f −1 (x) = y ⇔ f (y) = x
Eğer y = x3 ise,
(2)
yazarız.Tanımda y yi ve (2) de x i yerine koyarak, yok etme
kuralları olarak bilinen
f −1 (y) = f −1 (x3 ) = (x3 )1/3 = x
dir.
f −1
Uyarı :
gösterimindeki −1 bir kuvvet değildir. Başka bir
deyişle, f −1 ile 1/f (x) birbirine eşit değildir.
f −1 (f (x)) = x
f (f −1 (x)) = x
x∈A
x∈B
formüllerini elde ederiz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
84/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
85/ 110
Örnek
Birebir fonksiyonun tersini bulmak
Örnek : f (x) = x3 + 2 fonksiyonunun tersini bulunuz.
Çözüm: Yukarıda verilen adımlara uyarak, önce
ADIM 1
y = f (x) yazınız.
ADIM 2
Bu denklemde x i y cinsinden çözünüz (olanaklıysa).
ADIM 3 f −1 fonksiyonunu x in fonksiyonu olarak yazabilmek
için x ve y nin yerlerini değiştiriniz. Bu da y = f −1 (x) biçiminde
bir ifade verir.
y = x3 + 2
yazarız. Sonra, bu denklemi x için çözeriz:
x3 = y − 2
x =
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
86/ 110
Örnek...
Öğr.Gör.Dr. Meltem Altunkaynak
√
3
y−2
MAT 1009 Matematik I
87/ 110
Ters Fonksiyonlar ve Logaritmalar
f fonksiyonunun tersini bulma adımlarında x ile y nin yerlerini
değiştirme adımı, bize f −1 fonksiyonunun grafiğini f nin
grafiğinden bulma yöntemini de verir.
x=
p
3
y−2
Son olarak, x ile y nin yerlerini değiştiririz:
√
y = 3x−2
Dolayısıyla, verilen fonksiyonun tersi f −1 (x) =
Öğr.Gör.Dr. Meltem Altunkaynak
√
3
MAT 1009 Matematik I
f (a) = b için yeterli ve gerekli
koşul f −1 (b) = a olduğundan,
(a, b) noktasının f nin grafiği
üzerinde olması için yeterli ve
gerekli koşul (b, a) noktasının
f −1 in grafiği üzerinde olmasıdır.
Diğer yandan (b, a) noktasının
y = x doğrusuna göre
yansımasıdır.
x − 2 dir.
88/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
89/ 110
Örnek
Ters Fonksiyonlar ve Logaritmalar
√
Örnek: Aynı düzlemde f (x) = −1 − x fonksiyonunun ve tersinin
grafiklerini çiziniz.
√
Çözüm: Önce, y = −1 − x eğrisini (y 2 = −1 − x, ya da
x = −y 2 − 1 parabolünün üst yarı kolu) çizeriz. Daha sonra bunu
y = x doğrusuna yansıtıp, f −1 in grafiğini buluruz.
f nin grafiğinin y = x doğrusuna göre yansıması, f −1
fonksiyonunun grafiğini verir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
90/ 110
Örnek...
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
91/ 110
Logaritma Fonksiyonları
Grafiği doğrulama amacıyla, f −1 in ifadesinin, x > 0 için
f −1 (x) = −x2 − 1 olduğuna dikkat ediniz. Dolayısıyla, f −1
fonksiyonunun grafiği, y = −x2 − 1 parabolünün sağ yarı koludur,
ve bu sonuç grafik uyumludur.
a > 0 ve a 6= 1 için, f (x) = ax fonksiyonu artan veya azalan
olduğundan, Yatay Doğru Ölçütü gereğince, bire-birdir. Bu
nedenle, tersi f −1 vardır.
Bu fonksiyona a tabanına göre logaritma fonksiyonu adı verilir
ve
loga
ile gösterilir.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
92/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
93/ 110
Logaritma Fonksiyonları
Logaritma Fonksiyonları
Ters fonksiyon için
f −1 (x) = y ⇐⇒ f (y) = x
Yok etme kuralları f (x) = ax ve f −1 (x) = loga x özelinde
kullanılırsa
koşulunu kullanırsak,
loga (ax ) = x ,
loga x = y ⇐⇒ ay = x
elde ederiz.
aloga x = x ,
x∈R
x > 0 elde edilir.
Bu nedenle, 0 < x için loga x, a tabanının x sayısını vermesi için
gerekli olan üssüdür.
Örneğin 10−3 = 0, 001 olduğundan, log10 0.001 = −3 dür.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
94/ 110
Logaritma Fonksiyonları
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
95/ 110
Logaritma Fonksiyonları
loga x logaritma fonksiyonunun tanım kümesi (0, ∞), görüntü
kümesi ise R dir. Grafiği ise y = ax fonksiyonunun y = x
doğrusuna göre yansımasıdır.
Şekil 13, 1 < a için bir örnektir. ( En önemli logaritma
fonksiyonlarının tabanı a > 1 dir.)
0 < x için y = ax
fonksiyonu çok artan bir
fonksiyon olduğundan,
1 < x değerleri için
y = loga x fonksiyonu çok
yavaş artan bir
fonksiyondur.
Şekil 14:
Şekil 13:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
96/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
97/ 110
Logaritma Fonksiyonları
Logaritma Kuralları
Şekil 14, a sayısının farklı değerleri için loga x fonksiyonlarının
grfiklerini vermektedir.
loga 1 = 0 olduğundan, tüm logaritma fonksiyonlarının grafikleri
(1, 0) noktasından geçerler.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
98/ 110
Doğal Logaritma
x ve y pozitif sayılar için
1
2
3
loga (xy) = loga x + loga y
x
= loga x − loga y
loga
y
loga (xr ) = r loga x (Burada r gerçel sayıdır.)
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
99/ 110
Doğal Logaritma
e tabanına göre logaritmaya doğal logaritma denir ve özel bir
göseterime sahiptir:
Özel olarak x = 1 alırsak,
loge x = ln x
ln e = 1
doğal logaritma fonksiyonunu tanımlayan özellikler
elde ederiz. Herhangi tabana göre logaritmayı aşağıdaki gibi ifade
edebiliriz.
ln x = y ⇐⇒ ey = x
ln(ex ) = x
eln x = x
x∈R
ln x
,
ln a
a > 0, a 6= 1
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
loga x =
x>0
biçimini alır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
100/ 110
101/ 110
Örnek
Doğal Logaritma
Üstel fonksiyon y = ex in ve tersi doğal logaritma fonksiyonunun
grafikleri Şekil 15 de gösterilmiştir. y = ex eğrisi, y− eksenini 1
eğimle kestiğinden, y = ln x eğrisi, x− eksenini 1 eğimle keser.
Örnek: y = ln(x − 2) − 1 fonksiyonunun grafiğini çiziniz.
Çözüm: Şekil 15 te verilen y = ln x fonksiyonunun grafiğini sağ
tarafa iki birim kaydırarak y = ln(x − 2) grafiğini, sonra da aşağıya
bir birim kaydırarak y = ln(x − 2) − 1 fonksiyonunun grafiğini elde
ederiz.
Şekil 15:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
102/ 110
Doğal Logaritma
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
103/ 110
Parametrik Eğriler
Artan bir fonksiyon olan ln x, 1 < x değerleri için çok yavaş artar.
ln x, x in tün pozitif kuvvet fonksiyonlarından daha yavaş büyür.
√
Bu gerçeği görmek için y = ln x ve y = x1/2 = x fonksiyonlarının
grafikleri Şekil 16 ve 17 da çizilmiştir. Başlangıçta iki fonksiyon da
benzer davranış gösterirken, daha sonra kök fonksiyonunun
logaritmadan daha hızlı büyüdüğü görülmektedir.
Bir parçacığın Şekil 18 deki C eğrisi üzrinde hareket ettiğini
varsayalım.
Şekil 18:
Şekil 16:
Öğr.Gör.Dr. Meltem Altunkaynak
C eğrisi, Düşet Doğru Ölçütü nedeni ile y = f (x) gibi bir
denklemle betimlenemez. Ama parçacığın x− ve y− koordinatları
zamanın fonksiyonlarıdır, ve dolayısıyla x = f (t) ve y = f (t)
yazabiliriz.
Şekil 17:
MAT 1009 Matematik I
104/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
105/ 110
Parametrik Eğriler
Parametrik Eğriler
Böyle bir denklem çifti, bir eğriyi betimlemek için çoğu zaman
uygun bir yoldur ve aşağıdaki gibi tanımlanır.
x ve y üçüncü bir değişken ( parametre olarak adlandırılan) t nin
fonksiyonları olarak
x = f (t)
y = g(t)
t ile gösterilen parametrenin her zaman zamanı göstermesi şart
değildir ve aslında parametre için t den başka harfide
kullanabilirdik.
Yinede çoğu uygulamada t zamanı gösterir ve bu nedenle,
(x, y) = (f (t), g(t)) gösterimini bir parçacığın t zamanındaki
konumu olarak yorumlayabiliriz.
(parametrik denklemler olarak adlandırılan) denklemleriyle
verilmiş olsun.
t nin her değeri düzlemde bir (x, y) noktası belirler. t değiştikçe
(x, y) = (f (t), g(t)) noktalarıda değişir ve bir C eğrisi izler.
x = f (t)
y = g(t)
a6t6b
parametrik denklemleri ile betimlenen eğrinin başlangıç noktası
(f (a), g(a)), bitiş noktası ise (f (b), g(b)) dir.
Böyle tanımlanan eğrilere parametrik eğri diyeceğiz.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
Öğr.Gör.Dr. Meltem Altunkaynak
106/ 110
Örnek
MAT 1009 Matematik I
107/ 110
Örnek...
Bu örnekte parametre t, Şekil 19 de gösterildiği gibi, (radyan
olarak ölçülen) açı olarak yorumlanabilir.
Örnek: Parametrik denklemleri x = cos t, y = sin t, 0 6 t 6 2π
olan eğriyi bulunuz.
Çözüm: Üzerinde belirleyeceğimiz noktaları birleştirerek fikir sahibi
olabileceğimiz bir eğrinin bir daire olabileceği anlaşılıyor. Bu savı
doğrulamak için yine parametre t yi yok edelim.
x2 + y 2 = cos2 t + sin2 t = 1.
Buna göre, (x, y) noktası birim çember x2 + y 2 = 1 üzerinde
hareket eder.
Şekil 19:
t değerleri 0 dan 2π ye artarken, (x, y) = (cos t, sin t) noktası
çemberin üzerinde (1,0) noktasından başlayıp saat yönünün tersi
yönünde bir kere dolanır.
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
108/ 110
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
109/ 110
Örnek
Örnek:(Sikloid) Bir çember, düzgün bir doğru üzerinde
yuvarlanarak hareket ederken, çember üzerindeki P noktasının
izlediği eğriye sikloid denir (bkz. Şekil 20). Çemberin yarıçapı r
ise, ve çember x− ekseni üzerinde yuvarlanıyor ve P noktasının bir
konumu başlangıç noktasıysa, sikloidin parametrik denklemi
x = r(θ − sin θ)
y = r(1 − cos θ)
θ∈R
olarak elde edilir.
Şekil 20:
Öğr.Gör.Dr. Meltem Altunkaynak
MAT 1009 Matematik I
110/ 110

Bir Fonksiyonun Dört Farklı Gösterimi Bir Fonksiyonun Dört Farklı

Products

Support

Bir Fonksiyonun Dört Farklı Gösterimi Bir Fonksiyonun Dört Farklı

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib