˙Integralin Uygulamaları

Bölüm 1
İntegralin Uygulamaları
1.1
Alan
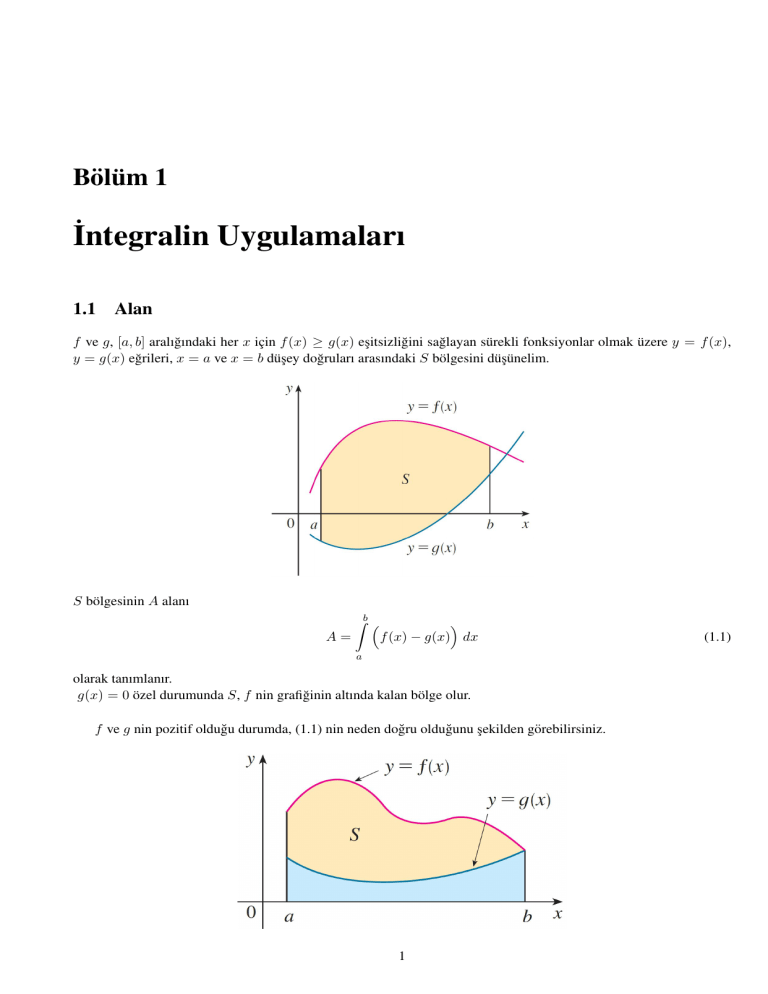
f ve g, [a, b] aralığındaki her x için f (x) ≥ g(x) eşitsizliğini sağlayan sürekli fonksiyonlar olmak üzere y = f (x),
y = g(x) eğrileri, x = a ve x = b düşey doğruları arasındaki S bölgesini düşünelim.
S bölgesinin A alanı
A=
Zb f (x) − g(x) dx
a
olarak tanımlanır.
g(x) = 0 özel durumunda S, f nin grafiğinin altında kalan bölge olur.
f ve g nin pozitif olduğu durumda, (1.1) nin neden doğru olduğunu şekilden görebilirsiniz.
1
(1.1)
2
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
S = y = f (x) in altında kalan alan − y = g(x) in altında kalan alan
Zb
Zb
f (x) dx −
=
a
g(x) dx =
a
Zb f (x) − g(x) dx
a
Örnek 1.
Üstten y = ex , alttan y = x ve kenarlardan x = 0 ve x = 1 ile sınırlı olan bölgenin alanını hesaplayınız.
Çözüm: Bölge, Şekil 1.1 de gösterilmiştir.
Şekil 1.1:
Üst sınır eğrisi y = ex ve alt sınır eğrisi y = x dir. Dolayısıyla, (1.1) deki formülde f (x) = ex , g(x) = x, a = 0,
ve b = 1 kullanırız:
Z1
1 2 1
x
x
A = (e − x) dx = e − x
2
0
0
=e−
1
− 1 = e − 1.5
2
1.1. ALAN
3
Örnek 2.
y = 2x − x2 ve y = x2 parabolleriyle sınırlı olan bölgenin alanını bulunuz.
Çözüm: Önce verilen denklemleri ortak çözerek, parabollerin kesiştikleri noktaları buluruz. Bu durumda,
x2 = 2x − x2 veya 2x2 − 2x = 0 elde ederiz. Böylece, 2x(x − 1) = 0 ve dolayısıyla x = 0 veya x = 1
buluruz. Kesişim noktaları (0, 0) ve (1, 1) dir.
Şekil 1.2:
Şekil 1.2 de gördüğümüz gibi üst ve alt sınırlar
yüst = 2x − x2
yalt = x2
ve
dir. Dolayısıyla toplam alan
Z1
Z1
2
(2x − 2x ) dx = 2
A =
0
0
x2 x3
=2
−
2
3
olur.
(x − x2 ) dx
1
=2
0
1 1
−
2 3
=
1
3
4
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Bazı bölgelerle çalışmak için, x değişkenini y nin fonksiyonu olarak düşünmek gerekir. f ve g sürekli ve her
c ≤ y ≤ d için f (y) ≥ g(y) olmak üzere, x = f (y), x = g(y), y = c ve y = d denklemleriyle sınırlı olan bölgenin
alanı
A=
Zd f (y) − g(y) dy
c
olur.
Örnek 3.
y = x − 1 doğrusu ve y 2 = 2x + 6 parabolüyle sınırlı olan bölgenin alanını bulunuz.
Çözüm: İki denklemi ortak çözersek, kesişim noktalarını (−1, −2) ve (5, 4) olarak buluruz.
Şekil 1.3:
Parabolün denklemini x için çözeriz ve Şekil 1.3 den sağ ve sol sınır eğrilerini
1
xsol = y 2 − 3
2
ve
xsağ = y + 1
1.1. ALAN
5
olarak buluruz. İntegrali, uygun y değerleri y = −2 ve y = 4 arasında hesaplamalıyız. Böylece
Z4
(xsağ − xsol ) dy
A =
−2
Z4 Z4 1 2
1 2
=
(y + 1) − ( y − 3) dy =
− y + y + 4 dy
2
2
−2
1
=−
2
−2
y3
3
y2
+
+ 4y
2
4
−2
4
1
= − (64) + 8 + 16 − ( + 2 − 8) = 18
6
3
olarak buluruz.
Şekil 1.4:
Örnekteki alanı, y yerine x e göre integral alarak da bulabilirdik ama bu durumda hesaplamalar daha karmaşık
olurdu. Bölgeyi Şekil 1.4 de görüldüğü gibi, A1 ve A2 diye ikiye ayırmamız gerekirdi. Örnekte kullandığımız yöntem,
çok daha basit.
1.1.1
Parametrik eğrilerin Sınırladığı Alanlar
Zb
F (x) ≥ 0 olduğu zaman, a dan b ye y = F (x) eğrisinin altında kalan alanın A =
F (x) dx olduğunu biliyoruz.
a
Eğer eğri
x = f (t),
y = g(t),
α≤t≤β
parametrik denklemleriyle tanımlanmışsa, o zaman Belirli İntegraller İçin Yerine Koyma Kuralı’nı kullanarak, alan
formülünü şöyle hesaplayabiliriz:


Zb
Zβ
Zα


g(t) f 0 (t) dt
A = y dx = g(t) f 0 (t) dt
ya da
a
α
β
6
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Örnek 4.
x = r(θ − sin θ)
y = r(1 − cos θ)
sikliodinin bir yayının altında kalan alanı bulunuz. (Bkz. Şekil 1.5)
Şekil 1.5:
Proof. Çözüm: Sikliodin bir yayı, 0 ≤ θ ≤ 2π değerleriyle elde edilir. y = r(1 − cos θ) ve dx = r(1 − cos θ) dθ ile
Yerine Kouma Kuralı’nı kullanırsak,
Z2π
A =
Z2π
r(1 − cos θ)r(1 − cos θ) dθ
y dx =
0
0
Z2π
Z2π
= r2 (1 − cos θ)2 dθ = r2 (1 − 2 cos θ + cos2 θ)dθ
0
0
Z2π 1
=r
1 − 2 cos θ + (1 + cos 2θ) dθ
2
2
0
= r2
= r2
olarak buluruz.
3
1
θ − 2 sin θ + sin 2θ
2
4
3
· 2π
2
= 3πr2
2π
0
1.1. ALAN
Alıştırmalar
Aşağıda verilen grafiklerdeki taralı bölgelerin alanlarını hesaplayınız.
7
8
1.2
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Hacimler
S yi bir düzlemle kesip, S nin kesiti dediğimiz düzlemsel bölgeyi elde ederek başlayacağız. a ≤ x ≤ b olmak üzere,
x-eksenine dik ve x noktasından geçen Px düzlemindeki S nin kesitinin alanı A(x) olsun. (Bkz. Şekil 1.6. S yi x
ten geçen bir bıçakla dilimlediğimizi ve bu dilimin alanını hesapladığımız düşününüz.) x, a dan b ye arttıkça, kesitin
alanı A(x) değişecektir.
Şekil 1.6:
Tanım 1.
S, x = a ve x = b arasında uzanan bir cisim olsun. A sürekli bir fonksiyon olmak üzere, x den geçen ve
x-eksenine dik olan Px düzlemindeki S nin kesitinin alanı A(x) ise, o zaman S nin hacmi
Zb
V =
A(x) dx
a
olarak tanımlanır.
Rb
V = A(x) dx formülünü kullandığımız zaman hatırlamamız gereken önemli nokta, A(x) in, x den
a
geçen ve x-eksenine dik dilimlemeyle elde edilen kesitin alanı olmasıdır.
Örnek 5.
Yarıçapı r olan bir kürenin hacminin
4
V = πr3
3
olduğunu gösteriniz.
Çözüm: Küreyi, merkezi
√ başlangıç noktasında olacak şekilde yerleştirirsek (bkz. Şekil 1.7), Px düzlemiyle kürenin
kesişimi, yarıçapı y = r2 − x2 olan bir çember olur (Pisagor Teoremi’nden).
Dolayısıyla, bu kesitin alanı
A(x) = πy 2 = π(r2 − x2 )
1.2. HACIMLER
9
Şekil 1.7:
olur. a = −r ve b = r alarak hacim tanımını kullanırsak
Z r
Z r
π(r2 − x2 ) dx
A(x) dx =
V =
−r
−rZ
r
2
2
= 2π
(r − x ) dx
0
r
x3
r3
2
3
= 2π r x −
= 2π r −
3 0
3
4 3
= πr
3
Örnek 6.
√
y = x eğrisi, x-ekseni ve x = 1 doğrusuyla sınırlanan bölgeyi x-ekseni çevresinde döndürmekle elde
edilen cismin hacmini bulunuz.
Şekil 1.8:
10
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Şekil 1.9:
Çözüm: Bölge, Şekil 1.8 da gösterilmiştir.Eğer x-ekseni çevresinde döndürülürse, Şekil 1.9 deki cismi elde ederiz.
√
x den geçen kesit, yarıçapı x olan bir çemberdir. Bu kesitin alanı
√
A(x) = π( x)2 = πx
olur. Bu cisim x = 0 ile x = 1 arasındadır. Dolayısıyla hacmi
1
Z 1
Z 1
π
x2
=
V =
A(x) dx =
πx dx = π
2 0
2
0
0
Örnek 7.
y = x3 , y = 8 ve x = 0 ile sınırlı olan bölgeyi y-ekseni çevresinde döndürerek elde edilen cismin hacmini
bulunuz.
Şekil 1.10:
Çözüm: Bölge, Şekil 1.10 de, cisim ise Şekil 1.11 de gösterilmiştir. Bölge y-ekseni çevresinde döndürüldüğü için
y-eksenine dik biçimde dilimlemek ve integrali y ye göre almak daha mantıklı olur. y yüksekliğindeki kesit, yarıçapı
√
x olan çembersel bir disktir. x = 3 y olduğu için, y den geçen kesitin alanı
√
A(y) = πx2 = π( 3 y)2 = πy 2/3
1.2. HACIMLER
11
Şekil 1.11:
Cisim, y = 0 ve y = 8 arasında kaldığı için hacmi
Z 8
Z 8
V =
A(y) dy =
πy 2/3 dy
0
0
3 5/3 8 96π
=
=π y
5
5
0
olarak bulunur.
Örnek 8.
y = x ve y = x2 eğrileriyle çevrili olan R bölgesi, x-ekseni çevresinde döndürülmüştür. Oluşan cismin
hacmini bulunuz.
12
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Şekil 1.12:
Çözüm: y = x ve y = x2 eğrileri, (0, 0) ve (1, 1) noktalarında kesişir. Aralarındaki bölge, dönel cisim ve x-eksenine
dik olan kesit Şekil 1.12 de gösterilmiştir. Px düzlemindeki kesit, iç yarıçapı x2 ve dış yarıçapı x olan bir halka
şeklindedir. Dolayısıyla, alanını bulmak için büyük çemberin alanından küçük çemberin alanını çıkarırız.
A(x) = πx2 − π(x2 )2 = π(x2 − x4 )
Bu durumda,
Z
V
1
Z
1
A(x) dx =
π(x2 − x4 ) dx
0
1 0
x3 x5
2π
=π
−
=
3
5 0
15
=
elde ederiz.
1.3
Yay Uzunluğu
Tanım 2.
Parametrik denklemleri x = f (t), y = g(t), a 6 t 6 b, olan bir düzgün eğri, t parametresi a değerinden b
değerine doğru artarken tam olarak bir kez izleniyorsa, o zaman bu eğrinin uzunluğu
s
Z b 2 2
dy
dx
L=
+
dt dir.
(1.2)
dt
dt
a
1.3. YAY UZUNLUĞU
13
Örnek 9.
x = t2 , y = t3 eğrisinin (1, 1) ve (4, 8) noktaları arasındaki yayının uzunluğunu bulunuz. Bkz Şekil 1.13
Şekil 1.13:
Çözüm: 1 6 t 6 2 değerlerinin, eğrinin (1, 1) ve (4, 8) noktaları arasındaki parçasını verdiğini x = t2 ve y = t3
denklemlerinden görüyoruz. Dolayısıyla, yay uzunluğu formülü
Z
2
s
L=
1
Z
=
dx
dt
2
+
dy
dt
2
Z
dt =
2p
(2t)2 + (3t2 )2 dt
1
2p
4t2 + 9t4 dt
1
Z
2
=
p
t 4 + 9t2 dt
1
Z
2
=
p
t 4 + 9t2 dt
1
u = 4 + 9t2 değişken değişikliğini yaparsak, du = 18t dt olur. t = 1 olduğunda u = 13; t = 2 olduğunda u = 40
dır. Böylece
1
L=
18
=
Z
40 √
13
1 2 3/2
u du =
· u
18 3
40
13
i
√ 1 h 3/2
1 √
40 − 133/2 =
80 10 − 13 13
27
27
buluruz.
14
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Kural 1.
Elimizdeki eğri y = f (x), a 6 x 6 b denklemleriyle verilmişse, x değişkenini parametre olarak alabiliriz. O zaman parametrik denklemler x = x, y = f (x) olur ve denklem 1.2
s
2
Z b
dy
dx
(1.2)
1+
L=
dx
a
biçimin alır.
Örnek 10.
xy = 1 hiperbolünün (1, 1) noktasından (2, 1/2) noktasına kadar olan parçasının uzunluğunu yaklaşık
olarak hesaplayınız.
Çözüm: Elimizde
y=
dy
1
=− 2
dx
x
1
x
olduğu için formül (1) den uzunluğu
Z
2
r
L=
1
dy
1+
dx =
dx
2
Z
r
1+
1
1
dx ∼
= 1.1321
x4
olarak elde ederiz.
Kural 2.
Benzer biçimde bir eğrinin denklemi x = f (y), a 6 y 6 b ise, y değişkenini parametre olarak alabiliriz.
O zaman parametrik denklemler x = f (y), y = y olur ve uzunluk
s
Z b 2
dx
L=
+ 1 dy
(1.3)
dy
a
olur.
Formül (1.2),(1) ve (1.3) teki karekökten ötürü, yay uzunluğu hesabında ortaya çıkan integrali kesin olarak hesaplamak
çoğu zaman çok zordur veya olanaksızdır.
Örnek 11.
y 2 = x parabolünün (0, 0) noktasından (1, 1) noktasına kadar olan yayının uzunluğunu bulunuz.
Çözüm: x = y 2 olduğu için
dx
dy
= 2y olur ve formül (1.3)
Z
L=
0
verir.
1
s
dx
dy
2
Z
+ 1 dy =
0
1p
4y 2 + 1 dy ∼
= 1.478943
1.4. BIR FONKSIYONUN ORTALAMA DEĞERI
15
Örnek 12.
x = r(θ − sin θ), y = r(1 − cos θ) sikloidinin bir yayının uzunluğunu bulunuz.
Şekil 1.14:
Proof. Çözüm: Çözüm: Bir yayı 0 6 θ 6 2π parametre aralığıyla elde edildiğini daha önce görmüştük.
dx
dy
= r(1 − cos θ) ve
= r sin θ
dθ
dθ
olduğu için
2π
Z
s
L =
0
Z
dx
dθ
2
+
dy
dθ
2
dθ
2π
q
r2 (1 − cos θ)2 + r2 sin2 θ dθ
2π
q
r2 (1 − 2 cos θ + cos2 θ + sin2 θ) dθ
=
0
Z
=
0
Z
=r
2π
p
2(1 − cos θ) dθ = 8r.
0
1.4
Bir Fonksiyonun Ortalama Değeri
Sonlu sayıda y1 , y2 , · · · , yn sayılarının ortalama değerini hesaplamak çok kolaydır:
yort =
y1 + y2 + · · · + yn
n
Ancak, sonsuz tane sıcaklık ölçümünün olanaklı olduğu bir durumda bir günün ortalama sıcaklığını nasıl hesaplayacağız?
16
BÖLÜM 1. İNTEGRALIN UYGULAMALARI
Bir sıcaklık fonksiyonu T (t) nin grafiği ve ortalama sıcaklık Tort için bir tahmin şekil 1.15 de verilmiştir.
Şekil 1.15:
Burada t saat cinsinden T ◦ C cinsinden ölçülmüştür. T (t) fonksiyonu t anındaki sıcaklığı gösteriyorsa, sıcaklığın
ortalama sıcaklığa eşit olduğu belirli bir an olup olmadığını merak edebiliriz. Şekil 1.15 deki sıcaklık fonksiyonu
için böyle iki an olduğunu görüyoruz.Genel olarak, bir f fonksiyonunun değerini tam olarak o fonksiyonun ortalama
değerine eşit olduğu, yani f (c) = fort olduğu bir c sayısı varmıdır.
Theorem 1 (İntegraller için Ortalama Değer Teoremi).
f, [a, b] aralığında sürekli bir fonksiyon ise [a, b] aralığında
f (c) = fort
1
=
b−a
Z
b
f (x) dx
a
eşitliğini yani
Z
b
f (x) dx = f (c)(b − a)
a
eşitliğini sağlayan bir c sayısı vardır.
Örneğin f (x) = 1 + x2 fonksiyonu [−1, 2] aralığında sürekli olduğu için, integraller için ortalama değer teoremine
göre, [−1, 2] aralığında
Z 2
(1 + x2 ) dx = f (c)[2 − (−1)]
−1
eşitliğini sağlayan bir c sayısı vardır. Bu özel durumda, c sayısını kesin olarak bulabiliriz.
2
x3
= 3f (c)
x+
3 −1
eşitliğinden f (c) = fort = 2 bulunur. Dolayısıyla 1 + c2 = 2 olduğundan c = ±1 olarak bulunur.
1.4. BIR FONKSIYONUN ORTALAMA DEĞERI
17
Örnek 13.
Bir cismin hızı aşağıdaki parametrik denklemle verilmiştir.(t zaman)
x = t,
y = t3/2
Harekete başlayıp 4sn hareket ederse, bu süre içerisindeki ortalama hızı nedir?
Çözüm: Ortalama hız
1
b−a
Z
b
y dx
a
formulüyle bulunabilir. Parametrik denklem kullanılırsa x = t ⇒ dx = dt
!
Z 4
1 t5/2 4
1
3/2
t dt =
= 16/5
Vort =
4−0 0
4 5/2 0