Vektör Demeti Vektör demeti kavraminin

Vektör Demeti
Vektör demeti kavraminin taniminina girmeden önce teki yi göz önüne alarak tanjant vektörleri
düsünelim.Her
için tanjant düzlemi vardir.Bu sifir vektörü olan vektörlü 2-boyutlu bir
vektör uzayidir.
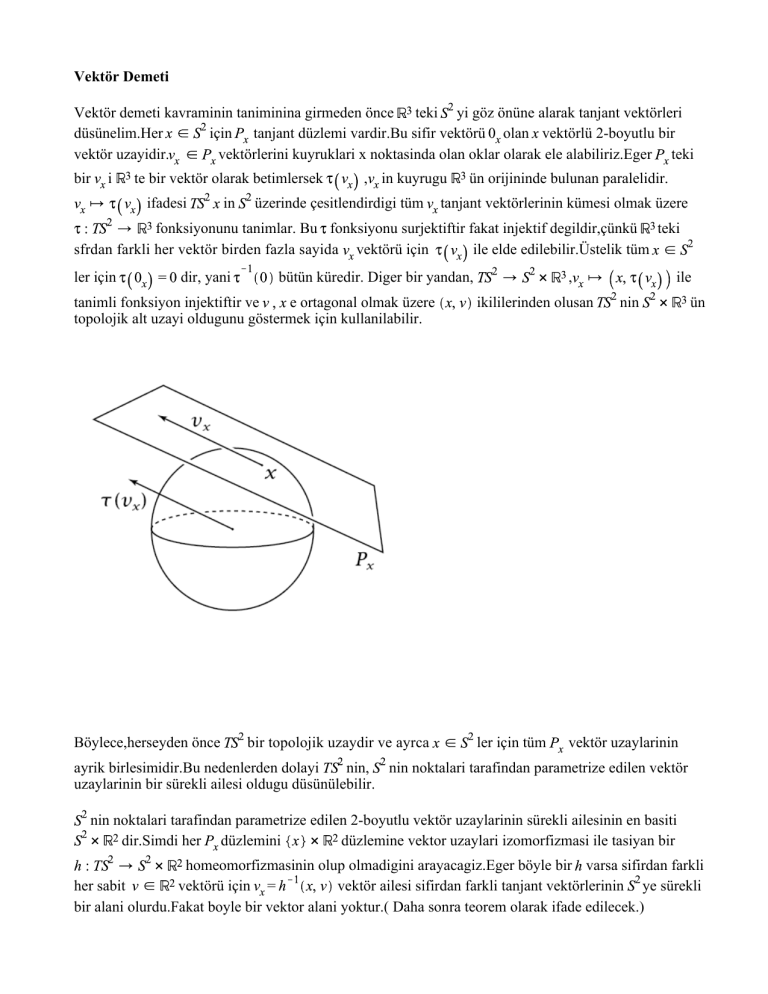
vektörlerini kuyruklari x noktasinda olan oklar olarak ele alabiliriz.Eger teki
bir
i
te bir vektör olarak betimlersek
ifadesi
in
, in kuyrugu
üzerinde çesitlendirdigi tüm
ün orijininde bulunan paralelidir.
tanjant vektörlerinin kümesi olmak üzere
fonksiyonunu tanimlar. Bu fonksiyonu surjektiftir fakat injektif degildir,çünkü teki
sfrdan farkli her vektör birden fazla sayida vektörü için
ile elde edilebilir.Üstelik tüm
ler için
dir, yani
bütün küredir. Diger bir yandan,
,
tanimli fonksiyon injektiftir ve
e ortagonal olmak üzere
topolojik alt uzayi oldugunu göstermek için kullanilabilir.
ikililerinden olusan
Böylece,herseyden önce
ler için tüm
bir topolojik uzaydir ve ayrca
ile
nin
ün
vektör uzaylarinin
ayrik birlesimidir.Bu nedenlerden dolayi
nin, nin noktalari tarafindan parametrize edilen vektör
uzaylarinin bir sürekli ailesi oldugu düsünülebilir.
nin noktalari tarafindan parametrize edilen 2-boyutlu vektör uzaylarinin sürekli ailesinin en basiti
dir.Simdi her düzlemini
düzlemine vektor uzaylari izomorfizmasi ile tasiyan bir
homeomorfizmasinin olup olmadigini arayacagiz.Eger böyle bir varsa sifirdan farkli
her sabit
vektörü için
vektör ailesi sifirdan farkli tanjant vektörlerinin ye sürekli
bir alani olurdu.Fakat boyle bir vektor alani yoktur.( Daha sonra teorem olarak ifade edilecek.)
Boyutu düsürerek benzer kavramlar
için de düsünülebilinir.Bu durumda sifirdan farkli e tanjant
vektörlerin bir sürekli alani vardir.Bu alan
noktalarini birim kompleks sayilar alarak ve i
vektörünün kuyrugu noktasinda olan translasyonu olarak düsünerek elde edilir.Bu ise
yi e
götüren
homeomorfizmasini meydana getirir ve
lineer izomorfizma ile gider.Yani
çarpimina denktir.
teki tanjant dogrusuna bir
e geçecek olursak burada yine
ün
e denk oldugunu gorecegiz.
denklik
homeomorfizmasi ile saglanir ve bu homeomorfizma
kuyrugu de olan
ü dörtlüler ile betimlersek
ü vektörün
translasyonuna götürür.Buna benzer yapilar kullanarak
nin
ye denk oldugu söylenebilir.
Her ne kadar
e genelde denk olmasa da bunun ksmen dogru oldugu bir yaklasim da vardir.
Örnegin yi ele alalim.Bir
noktas için tanjant düzleminin orijinden geçen translasyonu
olsun.