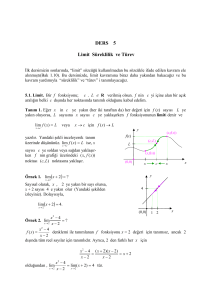
Türevin Uygu

Türevin Uygulamaları
A. Artan Ve Azalan Fonksiyonlar
i) Her x1, x2 A için, x1<x2 iken, f(x1)< f(x2) ise,
fonksiyonu, A kümesinde, artandır.
m=tan= f ’(x1)>0 ise, f fonksiyonu (a,b)
aralığında artandır.
ii) Her x1, x2 A için, x1<x2 iken, f(x1)> f(x2) ise, f
fonksiyonu, A kümesinde, azalandır.
m=tan= f ’(x1)<0 ise, f fonksiyonu (a,b)
aralığında azalandır.
Sonuç:
f:[a,b]R fonksiyonu, (a,b) aralığında artan ve türevli ise,
fonksiyonun bu aralıktaki türevi pozitiftir
Yani; f fonksiyonu, (a,b) aralığında artan bir fonksiyon ise
bu aralığın her elemanı için f’(x)>0’dır.
a
b
f’(x)
+++++
f(x)
artan
Sonuç:
f:[a,b]R, fonksiyonu, (a,b) aralığında azalan ve türevli
ise, fonksiyonun bu aralıktaki türevi negatiftir.
Yani; f fonksiyonu, (a,b) aralığında azalan fonksiyon ise
bu aralığın her elemanı için, f’(x)<0’dır.
a
b
f’(x)
-----
f(x)
azalan
Uygulamalar
Soru: f(x)=x2-2x fonksiyonunun artan veya
azalan olduğu aralıkları bulunuz?
Çözüm::
Fonksiyonunun, artan veya azalan olduğu aralıkları
bulabilmek için, türevinin işaretini incelemeliyiz.
f(x)=x2-2x  f’(x)= 2x-2
2x-2=0  x=1 olur.
-
f’(x)
f(x)
1
-
azalan
+
+
artan
mx  1
x 2
Soru: R-{-2} için, f(x)=
fonksiyonunun daima artan olabilmesi için, m ne olmalıdır?
Çözüm :
Fonksiyonun daima artan olabilmesi için, f’(x)>0 olmalıdır.
m.( x  2)  1.(mx  1)
mx  2m  mx  1
2m  1
f’(x)=
=
= ( x  2) 2
( x  2) 2
( x  2) 2
2m  1
0
Buradan;
2
( x  2)

2m  1  0

m
1
2
bulunur.
Soru :
y
Y=f(x)
-3 -2
-1
0
1
2
3
4
x
Şekilde, y=f(x) fonksiyonunun [-3,4] aralığındaki grafiğini görmektesiniz.Bu grafiğe göre, f(x)’in türevinin
pozitif veya negatif olduğu aralıkları bulunuz?
Çözüm :
a) [-3,-1) aralığında,
Fonksiyon azalan olduğundan,f ’(x)< 0 ‘dır.
b) (-1,3) aralığında,
Fonksiyon artan olduğundan, f ‘(x) > 0’dır.
c) (3,4) aralığında,
Fonksiyon azalan olduğundan, f ’(x)< 0 ‘dır
Soru :
y
Y=f’(x)
-3
-2
-1
0
1
2
3
4
x
Şekilde, y=f(x) fonksiyonunun, [-3,4] aralığındaki türevinin grafiğini görmektesiniz. Grafiğe bakarak, f(x)’in artan ve azalan olduğu aralıkları bu
lunuz?
y
Çözüm :
a) [-3,-2) aralığında:
Y=f’
(x)
-3 -2
-1
0 1 2 3 4
x
f’(x) > 0 olduğundan, f(x) bu aralıkta artan’dır.
b) (-2,0) aralığında:
f’(x) < 0 olduğundan, f(x) bu aralıkta azalan’dır.
c) (0,4] aralığında:
x=3 noktası hariç, f’(x) > 0 olduğundan,f(x) bu aralıkta
artan’dır.
B.Maksimum Ve Minimum
Değerlerin Bulunması:
1. YEREL MAKSİMUM NOKTASI:
Tanım: f:[a,b]R, y=f(x) fonksiyonu verilsin. x0(a,b) ve
 > 0 olsun. f fonksiyonu, (x0- ,xo+ ) aralığında en büyük
değerini x0 noktasında alıyorsa, (x0,f(x0)) noktasında bir
yerel maksimumu vardır.
f(x0) değerine, fonksiyonun bir yerel maksimum değeri
denir.
a
f(x0)
f ’(x)
Y=f(x)
a
x0- 
x0
x o+ 
b
f(x)
x0
+
b
-
f(x0)
Maksimum
2. YEREL MİNİMUM NOKTASI:
Tanım:f:[a,b]R, y=f(x) fonksiyonu verilsin. x0(a,b) ve
 > 0 olsun. f fonksiyonu, (x0- ,xo+ ) aralığında en küçük
değerini x0 noktasında alıyorsa, (x0,f(x0)) noktasında bir
yerel minimumu vardır.
f(x0) değerine, fonksiyonun bir
denir.
yerel minimum degeri
a
f ’(x)
a
f(x0)
x o+ 
Y=f(x)
f(x)
x0
-
b
+
f(x0)
b
Minimum
Sonuç:
Yerel f(b)
maksimum
a
+
+
+
++ - +
c
-
f(c)
d
-
f(a)
-
-
-
- +
+
+
+
+
+
+
f(d) Yerel minimum
f ’(x)>0
f ’(x)<0
f ’(x)>0
y=f(x)
b
Uygulamalar
Soru :
f(x)= x3-3x2+1 fonksiyonunun yerel maksimum ve yerel
minimum noktalarını bulunuz?
Cözüm:
Önce, f(x)’in türevini alıp, türevin işaretini incelemeliyiz:
f’(x)= 3x2-6x = 0 
x1= 0 ve x2= 2
x1= 0  f(0)= 1
x2= 2  f(2)= -3
-
f’(x) +
0
f(x)
1
0
2
-
0
-3
+
+
Soru : y
+
- -4
-2 –1 0
3
Cözüm :
f’(x)
f(x)
Şekilde, y=f(x) fonksiyonunun türevinin grafiğini
görüyorsunuz. Bu grafiğe
bakarak, y=f(x) fonksiyo+x
5 nunun, yerel maksimum ve
y=f ’(x) yerel minimum noktalarını
bulunuz?
-4
-
5
+
-
C. İkinci Türevin Geometrik
Anlamı
f:[a,b] R fonksiyonu, (a,b) aralığında ikinci basamaktan
türevli olsun:
y=f(x)
B
A

a

x1
x2 b
Eğrinin çukurluk yönü yukarı doğru bakmaktadır.
a’dan b’ye, teğetlerin eğim açılarının büyüdüğüne dikkat!
y=f(x)
B
A

a

x1
x2 b
Bu teğetlerin eğimleri;
m1= tan=f’(x1)
ve
m2=tan=f’(x2)
  tan< tan  f’(x1) < f’(x2) ‘dir.
Yani;
x1< x2 için, f’(x1) < f’(x2) olduğundan, f’ fonksiyonu artan’dır.
f’ fonksiyonu artan olduğundan, türevi, f’’(x) > 0 ‘dır.
Şimdi de, eğrilik yönü aşağı doğru olan bir eğri inceleyelim:
B
A


a x1
x2
b
a’dan b’ye , teğetlerin eğim açılarının küçüldüğüne dikkat!
Bu teğetlerin eğimleri;
m1= tan=f’(x1) ve m2= tan =f’(x2) ‘dir.
B
A


  tan> tan
a x1

x2
b
f’(x1) > f’(x2) ‘dir.
Yani;
x1< x2 için, f’(x1) > f’(x2) olduğundan, f’ fonksiyonu azalan’dır.
f’ fonksiyonu azalan olduğundan, türevi, f’’(x) < 0 ‘dır.
SONUÇ:
Bir f fonksiyonu için, aralığın her noktasında, f’’(x)< 0
oluyorsa, f fonksiyonunun bu
aralıktaki grafiğinin çukurluk
yönü aşağı doğrudur.
Bir f fonksiyonu için, aralığın her noktasında, f’’(x)> 0
oluyorsa, f fonksiyonunun bu
aralıktaki grafiğinin çukurluk
yönü yukarı doğrudur.
f’’(x)< 0 Konkav(İç bükey) f’’(x)> 0 Konveks(Dış bükey)
Soru :
f:R R, f(x)= x3+x2-2x fonksiyonunun, konveks ve konkav
olduğu aralıkları araştırınız?
Çözüm :
Öncelikle, f’in ikinci türevini alıp, işaretini incelemeliyiz.
f’(x)=3x2+2x-2
f’’(x)=6x+2 = 0
x= -1/3
- 
f’’(x)
f(x)
-1/3
-
+
+
Bir önceki örnekte görüldüğü gibi, fonksiyon eğrisi, eğrilik
yönünü bazı noktalarda değiştirmektedir:
Tanım:
Bir f fonksiyonunun grafiğinin, çukurluğunun yön değiştirdiği ve fonksiyonun sürekli olduğu noktaya,
Dönüm (büküm) noktası
denir.
Şekilleri dikkatle inceleyiniz!!!
f(x0)
a
f(x0)
x0
0
f ’’(x)<0
b
f ’’(x)>0
f ’’(x0)=0
Dönüm noktası
0 a
x0
f ’’(x)>0
b
f ’’(x)<0
f ’’(x0)=yok
Dönüm noktası
DİKKAT: İkinci türevin işaret değiştirdiği nokta DÖNÜM noktasıdır.
Uygulamalar
1. f: RR, f(x)= x4+x3-2x fonksiyonunun, konveks ve
konkav olduğu aralıkları ve varsa, dönüm noktalarını
bulunuz?
Çözüm :
f’(x)= 4x3+3x2-2
f’’(x)= 12x2+6x
İkinci türevin kökleri:
12x2+6x=0
6x(2x+1) = 0
6x=0
(2x+1)= 0
x1= 0
x2=-1
x -
f’’(x)
+
-1/2
0
+
-
+
konkav
konveks
f(x)
konveks
Dönüm
noktası
Dönüm
noktası
2. f: RR, f(x)=(x-2)4 fonksiyonunun, varsa, dönüm
noktasını bulunuz?
Çözüm :
f’(x)=4(x-2)3
f’’(x)= 12(x-2)2
ve
12(x-2)2=0  x1=x2=2
x
f’’(x)
- 
+
2
+
+ 
f(x)
konveks
konveks
?
x=2 noktası, ikinci türevin kökü olduğu halde, dönüm
noktası değildir
Türev bu noktada, işaret değiştirmemektedir!
Yani; f’’(x0)=0 olması, x0 noktasının DÖNÜM noktası
olmasını gerektirmez!!!!
D. L’HOSPITAL KURALI
(TÜREVİN, LİMİT KAVRAMINDA KULLANIMI)
Tanım: f ve g , [b,c] aralığında sürekli ve (b,c) aralığında türevli iki, fonksiyon
olsun. f ve g fonksiyonları, a(b,c) olmak üzere, bir a noktasında türevli ve g’(a)0 olsun.
f'(x)
varsa,
xa g'( x)
lim f(x)  0, lim g(x)  0, ve lim
xa
xa
f(x)
lim
xa g( x)
=
f'(x)
lim
xa g'(x)
L’HOSPITAL KURALI
0
0


BELİRSİZLİK HALLERİNE UYGULANIR
Uygulamalar
1.
x 2  7 x  10
lim 2
x 2 x  3x  2
limitinin değerini bulunuz?
Çözüm :
x 2  7 x  10
0
lim 2
=
x 2 x  3x  2
0
belirsizliği var
2x  7
3
2.2  7
x 2  7 x  10
lim
 3
lim 2
=
=
=
x

2
x 2 x  3x  2
2.2  3
2x  3
1
2. lim
x0
x  1  1 limitinin değerini bulunuz?
x
Çözüm :
lim
x0
x 11
=
x
0
belirsizliği var
0
1
lim
x0
x 11
=
x
=
lim
x0
1
2 0 1
2 x 1
1
1
= 2
= xlim
0
1
2 x1
1  cos x
limitinin değerini bulunuz?
xπ
sin x
3. lim
Çözüm :
1  cos x
=
lim
xπ
sin x
0
belirsizliği var
0
1  cos x
lim
=
xπ
sin x
- sinx
cosx
 sinπ
cosπ
lim
xπ
0
=
=
1
0
4.
ln( x  1)
lim x
x e
 cos x
limitinin değerini bulunuz?
Çözüm :
ln( x  1)
lim x
=
x e
 cos x
ln( x  1)
lim x
x e
 cos x


belirsizliği var
1
x1
= xlim

ex - sinx
0
0

5. lim
x0
ln(sin x)
ln(sin 2x)
limitinin değerini bulunuz?
Çözüm :
ln(sin x)
=
lim
x  0 ln(sin 2x )


ln(sin x)
= lim
lim
x  0 ln(sin 2x )
x0
lim
x0
belirsizliği var
cosx/sinx
2cos2x/sin2x
cosx/sinx
= lim
x0
2cos2x/sin2x
Cosx.sin2x
2cos2x.sinx
lim
x0
lim
x0
Cosx.sin2x
2cos2x.sinx
2.sinx.cos2x
2cos2x.sinx
2sinx.cosx
2. 1
2. cos 2 0
=
=
=
2. cos( 2.0 )
2. 1
1
1
x
lim

e
6.
x x
limitinin değerini bulunuz?
Çözüm :
1
lim
 ex = 0 
x x
1
lim
 ex =
x x
ex
lim
=
x x

ex 
lim
=
x x

ex
lim
x
1
e
=
= = 
1
1
7. lim x. sin
x 
 x2  limitinin değerini bulunuz?
Çözüm :
lim x. sin  x2  =  
x 
2
sin( )
0
x
lim
=
x
1
0
x
2
2
2
sin( )
 cos
2
x
x = lim 2. cos( 2 / x) = 2
x
lim
= lim
x
x
1
x
1
2
x
x
8.
1 
 1
lim 

 limitinin değerini bulunuz?
x  1 x  1
ln x 
Çözüm :
1 
 1
lim 

 =
x  1 x  1
ln x 
1 
 1
lim 

 =
x  1 x  1
ln x 
- 
0
 ln x  x  1 
 =
lim 
x  1 ln x  ( x  1)
0


 ln x  x  1 
 =
lim 
x  1 ln x  ( x  1)


lim
x 1
1  x
x
( x  1)  x. ln x
x
lim
x 1
1
 1
x
1
 ( x  1)  ln x
x
1 x
= lim
=
x  1 ( x  1)  x. ln x
=
0
0
Bu aşamada, L’Hospital kuralı bir kere daha uygulanır:
1 x
lim
=
x  1 ( x  1)  x. ln x
lim
x 1
1
x2
1 1
 2
x x
 1
2
1
 1
x
lim
= lim
=
x 1 x  1
x 1 x  1
2
x2
=