x - SABİS - Sakarya Üniversitesi
advertisement

İSTATİSTİK
7. BÖLÜM
SÜREKLİ RASSAL DEĞİŞKENLER
Doç. Dr. Şakir GÖRMÜŞ
2013
2
Yedinci Bölüm
Sakarya Üniversitesi
SÜREKLİ RASSAL
DEĞİŞKENLER
Öğrenme Hedefleri
Bu bölümü çalıştıktan sonra;
-
Sürekli Rassal değişken kavramını açıklayabilir.
Sürekli rassal değişkenlerin olasılıklarını hesaplayabilir.
Normal dağılımı açıklayabilir ve hesaplayabilir.
Merkezi Limit Teoremini açıklayabilir.
Temel Kavramlar
Sürekli Rassal değişken
Normal dağılımı
Merkezi Limit Teoremi
İçindekiler
1.
SÜREKLİ RASSAL DEĞİŞKENLER
2.
SÜREKLİ RASSAL DEĞİŞKENLERİN OLASILIK
DAĞILIMLARI
2.1. Birikimli Olasılık Fonksiyonu
2.2. Aralık Olasılığı ve Birikimli Olasılık Fonksiyonu
2.3.Olasılık Yoğunluk Fonksiyonu
3.
NORMAL DAĞILIM
3.1. Normal Dağılım Olasılık Yoğunluk Fonksiyonu
3.2. Normal Dağılımın Özellikleri
3.3. Normal Rassal Değişkenlerin Aralık Olasılıkları
3.4. Standart Normal Dağılım
4.
MERKEZİ LİMİT TEOREMİ
Temel İstatiksel Kavramlar
1. SÜREKLİ RASSAL DEĞİŞKENLER
Bu bölümde belli bir sayı çizgisi aralığında bütün değerleri alabilen değişkenler
incelenecektir ki bu değişkenlere “Sürekli Rassal Değişkenler” denir. Zaman, uzaklık,
sıcaklık, boy, kilo vb. ölçüler sürekli rassal değişkene örnek olarak verilebilir.
Genellikle sürekli rassal değişkenlerin belli bir aralıkta olma olasılığı bu bölümde ilgi
alanımızdır.
Örneğin;
Rassal olarak seçilen bir öğrencinin not ortalamasının 85-90 arasında olma
olasılığı
Rassal olarak seçilen bir ailenin yıllık gelirinin 15000-20000 TL arasında olma
olasılığı
Rassal olarak seçilen bir öğrencinin not ortalamasının 50’den düşük olma
olasılığı
Rassal olarak seçilen bir ailenin yıllık gelirinin 20000 TL’den yüksek olma
olasılığı gibi
2. SÜREKLİ RASSAL DEĞİŞKENLERİN OLASILIK DAĞILIMLARI
2.1. Birikimli Olasılık Fonksiyonu
X sürekli bir rassal değişkeni ve x ise bu değişkenin alabileceği belli bir değeri
göstermektedir. X’in Birikimli Olasılık Fonksiyonu, X sürekli rassal değişkeninin belli
bir x değerini aşmama olasılığını x’in bir fonksiyonu olarak verir.
X’in Birikimli Olasılık Fonksiyonu:
𝑥
F (x) = P (X ≤ x ) = ∫−∞ ƒ (𝑡)𝑑𝑡
2.2. Aralık Olasılığı ve Birikimli Olasılık Fonksiyonu
X sürekli rassal değişkeni a ve b gibi iki değer alabiliyorsa, rassal değişkenin bu iki
aralık arasında bir değer alma olasılığı,
P (a < X < b) = F (b) – F (a)
3
4
Sakarya Üniversitesi
2.3. Olasılık Yoğunluk Fonksiyonu
Uygulamada kolaylık sağladığı için “Olasılık Yoğunluk Fonksiyonu” daha yaygın
kullanılmaktadır.
X sürekli rassal değişkeninin belli bir aralıkta olma olasılığı “Olasılık Yoğunluk
Fonksiyonu” ile hesaplanabilir. Sürekli rassal bir değişkenin Olasılık Yoğunluk
Fonksiyonu aşağıdaki özelliklere sahiptir:
1. Olasılık Yoğunluk Fonksiyonu ƒ(x) ile gösterilir.
2. x’in bütün değerleri için ƒ(x) ≥ 0 (eğri yatay ekseni kesmez)
3. Olasılık Yoğunluk Fonksiyonu eğrisi altında kalan alan 1’e eşittir.
∞
∫ ƒ (𝑥 )𝑑𝑥 = 1
−∞
Temel İstatiksel Kavramlar
4. X rassal değişkeninin a ve b değerleri arasında bir değer olma olasılığı, Olasılık
Yoğunluk Fonksiyonu altında bu iki değer arasında kalan alandır. (a<b)
𝑏
P ( a < X < b ) = ∫𝑎 ƒ (𝑥 )𝑑𝑥
5
6
Sakarya Üniversitesi
ÖRNEK:
𝑐𝑥 2 ,
0≤𝑥≤3
0,
𝑑𝑖ğ𝑒𝑟 𝑥 𝑑𝑒ğ𝑒𝑟𝑙𝑒𝑟𝑖 𝑖ç𝑖𝑛
𝑓(𝑥) = {
a) Yukarıdaki fonksiyonun olasılık yoğunluk fonksiyonu olabilmesi için c
hangi değeri almalıdır?
𝑥
3
𝑓(𝑥) = ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑐𝑥 2 𝑑𝑥 = 1
−∞
=c (
𝑐=
0
x3 3
33
03
27
27
) |0 = c ( ) − c ( ) =
𝑐=
𝑐 = 1′𝑑𝑒𝑛
3
3
3
3
3
3
bulunur.
27
Temel İstatiksel Kavramlar
b) Olasılık yoğunluk fonksiyonunu gösteriniz?
3 2
𝑥 ,
27
𝑓(𝑥) = {
0,
0≤𝑥≤3
𝑑𝑖ğ𝑒𝑟 𝑥 𝑑𝑒ğ𝑒𝑟𝑙𝑒𝑟𝑖 𝑖ç𝑖𝑛
c) F (x) kümülatif olasılık dağılım fonksiyonunu bulunuz?
𝑥
𝑥
𝐹(𝑥) = ∫ 𝑓(𝑡)𝑑𝑥 = ∫
−∞
0
3 2
3 t3 x
3 x3
𝑥3
𝑡 𝑑𝑥 = =
( ) |0 =
( ) =
27
27 3
27 3
27
d) F (2) ‘yi hesaplayınız?
𝐹 (2) = 𝑝 (𝑥 ≤ 2) =
3
27
23
(
3
) =
8
27
= 0.3
X rassal değişkeninin 2’den küçük olma olasılığı yüzde 30’dur.
7
8
Sakarya Üniversitesi
e) P ( x ≥ 1) ‘in olasılık yoğunluk fonksiyonunu hesaplayınız?
3
3 2
3 x3 3
𝑝 (𝑥 ≥ 1) = ∫
𝑥 𝑑𝑥 =
( ) |1
27
27
3
1
3 33
3 13
=
( )−
( )=
27 3
27 3
=
27
1
26
−
=
= 0.96
27 27 27
X rassal değişkeninin 1’den büyük olma olasılığı yüzde 96’dır.
Temel İstatiksel Kavramlar
f) P ( 1 ≤ X ≤ 2) ‘in olasılık yoğunluk fonksiyonunu hesaplayınız?
2
3 2
3 x3 2
𝑝 (1 ≤ 𝑥 ≤ 2) = ∫
𝑥 𝑑𝑥 =
( )|
27 3 1
1 27
3 23
3 13
8
1
7
=
( )−
( )=
−
=
27 3
27 3
27 27
27
= 0.26
X rassal değişkeninin 1ile 2 arasında olma olasılığı yüzde 26’dır.
9
10
Sakarya Üniversitesi
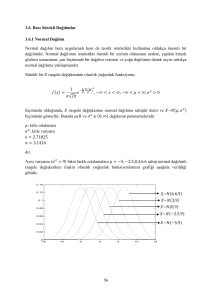
3. NORMAL DAĞILIM
Günlük hayatta karşılaşılan birçok olayın olasılık yoğunluk fonksiyonu aritmetik
ortalama etrafında yüksek ve uçlara doğru ise azalan bir seyir göstermektedir. Bu tür
dağılımlara “Normal Dağılım” denir ve istatistik analizlerinde en çok kullanılandır.
Normal olasılık yoğunluk fonksiyonu aşağıdaki şekilde görüldüğü üzere aritmetik
ortalama etrafında simetrik bir dağılıma sahiptir. Normal olasılık yoğunluk fonksiyonu
çana benzediğinden “Çan Eğrisi” olarak ta adlandırılır.
Eğrinin kuyrukları x eksenini sonsuzda keser ve eğrinin altında kalan alan 1’e eşittir.
Süreklilik gösteren olayların dağılımına uygundur ve tek maksimuma sahip olduğu için
Temel İstatiksel Kavramlar
çarpıklık ve basıklık katsayıları kolaylıkla hesaplanabilir ki buda çalışmalarda büyük
kolaylıklar sağlar.
3.1. Normal Dağılım Olasılık Yoğunluk Fonksiyonu
X rassal değişkeninin Normal dağılımın olasılık yoğunluk fonksiyonu aşağıda
verilmiştir.
𝑓 (𝑥 ) =
1
𝜎 √2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
,
- ∞ < x < ∞ için
Normal dağılımın olasılık yoğunluk fonksiyonunda yer alan sembollerin açıklanmaya
ihtiyacı vardır.
x = olasılığı hesaplanacak tesadüfi değişken
µ = X rassal değişkenin aritmetik ortalaması
σ2 = X rassal değişkeninin varyansı
e = 2.718 (tabii logaritmanın tabanı)
π = 3.141 (pi sayısı)
µ ve σ2, eksi sonsuz ile artı sonsuz arasında bir değer alabilir. Bundan dolayı tek bir
normal dağılım yoktur µ ve σ2 alacağı değerlere göre farklı olabilirler.
X rassal değişkeninin ortalaması µ ve varyansı σ2 olan normal dağılıma sahip ise bu
aşağıdaki şekilde gösterilir.
X N (μ ,σ2 )
X rassal değişkeninin istenilen bir aralıkta olma olasılığı aşağıdaki şekilde
hesaplanabilir.
11
12
Sakarya Üniversitesi
𝑏
1
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝜎√2𝜋
𝑎
𝑒
−
(𝑥− µ)2
2𝜎2
𝑑𝑥
X rassal değişkenin normal dağılıma sahip olduğundan olasılıklar Z (Normal dağılım
tablosu) tablosu yardımıyla daha kolay hesaplanabilir. Z =
𝑥− µ
𝜎
olarak ifade edilebilir.
X rassal değişkeninin istenilen bir aralıkta olma olasılığı aşağıdaki şekilde de ifade
edilebilir.
𝑏
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝑎
1
𝜎√2𝜋
𝑒
−
𝑍2
2
𝑑𝑥
3.2. Normal Dağılımın Özellikleri
X rassal değişkeninin ortalaması µ ve varyansı σ2 olan normal dağılıma uyduğu
düşünülürse aşağıdaki özelliklere sahip olacaktır.
1. X rassal değişkeninin ortalaması E (X) = µ
2. X rassal değişkeninin varyansı Var (X) = E [ ( X- µ )2 ] = σ2
3. Skewness = 0 (Basıklık katsayısı)
4. Kurtosis = 3 (Çarpıklık Katsayısı)
X rassal değişkeninin dağılımın ortalaması ve varyansı bu değişkenin olasılık
fonksiyonunun şeklini belirler. Dağılımın iki parametresi olan ortalama ve varyansı
değiştikçe normal dağılım grafiğinin şeklide aşağıdaki örneklerde görüldüğü üzere
değişecektir.
Temel İstatiksel Kavramlar
Şekil A’da normal dağılıma sahip ortalamaları aynı varyansları farklı iki tane olasılık
yoğunluk fonksiyonu verilmektedir. Şekilden de görüldüğü üzere varyans azaldıkça
olasılık yoğunluk fonksiyonu sivrileşmektedir (Basıklığı azalmaktadır).
Şekil B’de normal dağılıma sahip varyansları aynı ortalamaları farklı iki tane olasılık
yoğunluk fonksiyonu verilmektedir. Şekilden de görüldüğü üzere ortalama artıkça
yoğunluk fonksiyonu yana kayarken biçiminde herhangi bir değişme söz konusu
değildir.
13
14
Sakarya Üniversitesi
Yukarıdaki şekilde X rassal değişkeninin olasılık yoğunluk fonksiyonu normal dağılıma
sahiptir ve dört farklı şekilde verilmiştir. Ortalama ve standart sapmadaki değişmelere
göre olasılık yoğunluk fonksiyonu eğrisinin değişimleri net olarak görülmektedir.
3.3.Normal Rassal Değişkenlerin Kümülatif (Birikimli) Olasılık
Fonksiyonu
Ortalaması
µ
ve varyansı σ2 olan normal dağılıma sahip bir X rassal değişkeninin
Kümülatif olasılık fonksiyonu F (x) = P ( X ≤ x0 ) olarak gösterilir.
X rassal değişkeninin belli bir x0 değerinde küçük olma olasılığını gösterir.
Yukarıdaki şekilde gri taralı alan,
normal dağılıma sahip X rassal değişkeninin
herhangi bir x0 değerinden küçük olma olasılığını vermektedir. Bu alan aşağıdaki genel
formül yardımıyla bulunabilir.
𝑥0
𝐹 (𝑥 ) = 𝑃 (𝑋 ≤
𝑥0 )
= ∫
−∞
1
𝜎√2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
𝑑𝑥
Temel İstatiksel Kavramlar
3.4.Normal Rassal Değişkenlerin Aralıklı Olasılık Fonksiyonu
Ortalaması µ ve varyansı σ2 olan normal dağılıma sahip bir X rassal değişkeninin
aralıklı olasılık fonksiyonu F (a) – F (b) = P ( a < X < b ) olarak gösterilir.
X rassal değişkeninin a ve b gibi iki değer arasında olma olasılığını gösterir (a < b
koşuluyla).
Yukarıdaki şekilde gri taralı alan, normal dağılıma sahip X rassal değişkeninin a ve b
gibi iki değer arasında olma olasılığını vermektedir. Bu alan aşağıdaki genel formül
yardımıyla bulunabilir.
15
16
Sakarya Üniversitesi
𝑏
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝑎
1
𝜎√2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
𝑑𝑥
Dağılım normal bir dağılımsa o zaman aşağıdaki normal dağılım tablosu kullanılır.
Temel İstatiksel Kavramlar
17
18
Sakarya Üniversitesi
3.5.Standart Normal Dağılım
Normal olasılık fonksiyonlarını hesaplamak bazı güçlükler içerdiğinden her seferinde
bilgisayar yardımıyla sayısal yöntemler kullanılarak hesaplamamız gerekir. Bu işlemi
yapmak yerine standart normal dağılım (Z) tablosu kullanılabilir. Bu tablolarda her bir
normal olasılık dağılımının olasılıkları çizelgeleştirilmiş ve tek bir normal dağılım
olasılıklarıyla ifade edilmiştir.
X ortalaması 0 ve varyansı 1 olan normal rassal değişken ise Standart normal dağılıma
(Z) sahip demektir ve aşağıdaki şekilde gösterilir.
Z N (μ=0 ,σ2 =1)
X rassal değişkeninin Normal dağılımın olasılık yoğunluk fonksiyonu aşağıda
verilmiştir.
𝑓 (𝑧) =
1
√2𝜋
𝑒
−
𝑍2
2
,
- ∞ < x < ∞ için
Standart normal dağılımın olasılık yoğunluk fonksiyonunda yer alan sembollerin
açıklanmaya ihtiyacı vardır.
Z=
𝑋− µ
𝜎
E (Z) = µ = 0
Var (Z) = σ = 1
Z değeri belirli bir değerin aritmetik ortalamadan kaç standart sapma aşağıda ya da
yukarıda olduğunu belirlemek için kullanılır.
Temel İstatiksel Kavramlar
Yukarıdaki iki şekilde standart normal dağılıma sahiptir. Standart normal dağılım
Özellikleri:
1. Dağılım ortalamaya göre simetriktir. %50'si sağda, %50'si soldadır.
2.Normal dağılım eğrisinin altında kalan alan 1’e eşittir.
3. Aritmetik ortalama, ortanca, tepe değer (mod) birbirine eşittir ve maksimum
yüksekliğin bulunduğu yerdedir.
4. Normal dağılımı gösteren değişkenlerin aldıkları değerlerin;
19
20
Sakarya Üniversitesi
Gözlemlerin %68 ‘ i ortalama ile 1 standart sapma aralığına,
Gözlemlerin %95‘ i ortalama ile 2 standart sapma aralığına, ve
Gözlemlerin %99 ‘ i ortalama ile 3 standart sapma aralığına düşer.
Normal Dağılımın Standart Normal Dağılıma Çevrilmesi
Normal dağılımları standart normal dağılımlara kolaylıkla çevirebiliriz. Bu çevirme
işleminden sonrada olasılıkları standart normal dağılım (Z) tablosu yardımıyla
bulabiliriz.
ÖRNEK 1:
Sakarya Üniversitesi öğrencilerinin gelirleri normal dağılıma sahiptir. Ortalamasının (μ)
400 ve standart sapmanın (σ) 50 olduğu bilindiğine göre tesadüfü seçilen bir öğrencinin
geliri 500 (X) olsun. Bu normal dağılımı standart normal dağılıma çeviriniz.
Z=
𝑋− µ
𝜎
=
500−400
50
=2
Bu durumda seçilen öğrencinin geliri, ortalamadan 2 standart sapma daha yüksektir.
ÖRNEK 2:
Temel İstatiksel Kavramlar
Sakarya Üniversitesi öğrencilerinin gelirleri normal dağılıma sahiptir. Ortalamasının (μ)
400 ve standart sapmanın (σ) 50 olduğu bilindiğine göre tesadüfü seçilen bir öğrencinin
geliri 350 (X) olsun. Bu normal dağılımı standart normal dağılıma çeviriniz.
Z=
𝑋− µ
𝜎
=
350−400
50
= −1
Bu durumda seçilen öğrencinin geliri, ortalamadan 1 standart sapma düşüktür.
Standart normal dağılım tablosu aşağıda verilmiştir. Bu tabloyu okumayı bilmemiz
gerekir.
Z tablosu
•Artı eksi 3.49 arasında değişiyor.
•Bu, teorik evrenin %99.98’ine karşılık geliyor.
•Z tablosu 1/10’luk aralarla standart sapmayı gösteriyor
•Araştırmacılar z tablosundaki birkaç değerle ilgilenir. Çünkü çoğu hipotez testlerinde
%95 ve %99’luk alanlarla ilgileniyor.
21
22
Sakarya Üniversitesi
Tablo 1. Standart normal dağılım tablosu
z
.0
.01
.02
.03
.04
.05
.06
.07
.08
.09
.0
.5000
.5040
.5080
.5120
.5160
.5199
.5239
.5279
.5319
.5359
.1
.5398
.5438
.5578
.5517
.5557
.5596
.5636
.5675
.5714
.5753
.2
.5793
.5832
.5871
.5910
.5948
.5987
.6026
.6064
.6103
.6141
.3
.6179
.6217
.6255
.6293
.6331
.6368
.6406
.6443
.6480
.6517
.4
.6554
.6591
.6628
.6664
.6700
.6736
.6772
.6808
.6844
.6879
.5
.6915
.6950
.6985
.7019
.7054
.7088
.7123
.7157
.7190
.7224
.6
.7257
.7291
.7324
.7357
.7389
.7422
.7454
.7486
.7517
.7549
.7
.7580
.7611
.7642
.7673
.7704
.7734
.7764
.7794
.7823
.7852
Temel İstatiksel Kavramlar
.8
.7881
.7910
.7939
.7967
.7995
.8023
.8051
.8078
.8106
.8133
.9
.8159
.8186
.8212
.8238
.8264
.8289
.8315
.8340
.8365
.8389
1.0
.8413
.8438
.8461
.8485
.8508
.8531
.8554
.8577
.8599
.8621
1.1
.8643
.8665
.8686
.8708
.8729
.8749
.8770
.8790
.8810
.8830
1.2
.8849
.8869
.8888
.8907
.8925
.8944
.8962
.8980
.8997
.9015
1.3
.9032
.9049
.9066
.9082
.9099
.9115
.9131
.9147
.9162
.9177
1.4
.9192
.9207
.9222
.9236
.9251
.9265
.9279
.9292
.9306
.9319
1.5
.9332
.9345
.9357
.9370
.9382
.9394
.9406
.9418
.9429
.9441
1.6
.9452
.9463
.9474
.9484
.9495
.9505
.9515
.9525
.9535
.9545
1.7
.9554
.9564
.9573
.9582
.9591
.9599
.9608
.9616
.9625
.9633
1.8
.9641
.9649
.9656
.9664
.9671
.9678
.9686
.9693
.9699
.9706
1.9
.9713
.9719
.9726
.9732
.9738
.9744
.9750
.9756
.9761
.9767
2.0
.9772
.9778
.9783
.9788
.9793
.9798
.9803
.9808
.9812
.9817
2.1
.9821
.9826
.9830
.9834
.9838
.9842
.9846
.9850
.9854
.9857
2.2
.9861
.9864
.9868
.9871
.9875
.9878
.9881
.9884
.9887
.9890
23
24
Sakarya Üniversitesi
2.3
.9893
.9896
.9898
.9901
.9904
.9906
.9909
.9911
.9913
.9916
2.4
.9918
.9920
.9922
.9925
.9927
.9929
.9931
.9932
.9934
.9936
2.5
.9938
.9940
.9941
.9943
.9945
.9946
.9948
.9949
.9951
.9952
2.6
.9953
.9955
.9956
.9957
.9959
.9960
.9961
.9962
.9963
.9964
2.7
.9965
.9966
.9967
.9968
.9969
.9970
.9971
.9972
.9973
.9974
2.8
.9974
.9975
.9976
.9977
.9977
.9978
.9979
.9979
.9980
.9981
2.9
.9981
.9982
.9982
.9983
.9984
.9984
.9985
.9985
.9986
.9986
3.0
.9987
.9987
.9987
.9988
.9988
.9989
.9989
.9989
.9990
.9990
3.1
.9990
.9991
.9991
.9991
.9992
.9992
.9992
.9992
.9993
.9993
3.2
.9993
.9993
.9994
.9994
.9994
.9994
.9994
.9995
.9995
.9995
3.3
.9995
.9995
.9995
.9996
.9996
.9996
.9996
.9996
.9996
.9997
3.4
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9998
Yukarıdaki tabloda çeşitli Z değerleri için normal eğrilerin alanlarını hesaplanmıştır. Bu
tablolar yardımıyla doğrudan olasılıkları hesaplayabiliriz bunun için Z tablosunu
okumasını bilmemiz gerekir. Z tablosunun nasıl okunacağını aşağıdaki örnekler
yardımıyla daha iyi anlayabiliriz.
0.5 sayısı. 5 şeklinde yazılabilir. Aynı şekilde 0.59 sayısı. 59 şeklinde yazılabilir.
Temel İstatiksel Kavramlar
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z<0.68) olduğunu
varsayalım. Bunun için ilk önce mavi dikey ve mavi yatay sütunlara bakmalıyız.
0.68 bu sütunlarda .6 ve .08 noktalarının (.6 + .08 = .68) kesiştiği yerde aranır.
Böylece P(Z<0.68) = .7517 deriz.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z<1.36) olduğunu
varsayalım. Bunun için ilk önce mavi dikey ve mavi yatay sütunlara bakmalıyız.
1.36 bu sütunlarda 1.3 ve .06 noktalarının (1.3 + .06 = 1.24) kesiştiği yerde
aranır. Böylece P(Z<1.36) = .9131 deriz.
25
26
Sakarya Üniversitesi
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z>2.18) olduğunu
varsayalım. Bu olasılığı tabloda arayabilmenin tek koşulu P(Z<Z0) şeklinde
yazılabilmesidir. P(Z>2.18) = 1 - P(Z<2.18) = 1- 0.9854 = 0.0146 şeklinde
bulunur.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z< -1.36)
olduğunu varsayalım. Bu olasılığı tabloda arayabilmenin tek koşulu aranan
değerin pozitif olmasıdır. P(Z<-1.36) = 1 - P(Z<1.36) = 1- 0.9131 = 0.0869
şeklinde bulunur.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z>-2.96)
olduğunu varsayalım. Normal dağılımın simetri özelliğinden bu dağılım
P(Z<2.96) şeklinde yazılabilir.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(1.36<Z<1.96)
olduğunu varsayalım. Bu aralıklardaki olasılık P(Z<1.96) - P(Z<1.36) = 0.97500.9131 =0.0619 şeklinde bulunur.
Temel İstatiksel Kavramlar
Standart normal dağılıma dönüştürülen bir normal dağılımın P(-1.26<Z<1.26)
olduğunu varsayalım. Bu aralıklardaki olasılık P(Z<1.26) - [ 1 - P(Z<1.26) ] =
2P(Z<1.28) - 1 şeklinde bulunur.
4. MERKEZİ LİMİT TEOREMİ
Normal dağılıma sahip rassal değişkenlerde gözlem sayısı (n) artıkça rassal değişken
standart normal dağılıma yaklaşır.
İÇİNDEKİLER
5.
SÜREKLİ RASSAL DEĞİŞKENLER
6.
SÜREKLİ RASSAL DEĞİŞKENLERİN OLASILIK
DAĞILIMLARI
6.1. Birikimli Olasılık Fonksiyonu
27
28
Sakarya Üniversitesi
6.2. Aralık Olasılığı ve Birikimli Olasılık Fonksiyonu
6.3.Olasılık Yoğunluk Fonksiyonu
7.
NORMAL DAĞILIM
7.1. Normal Dağılım Olasılık Yoğunluk Fonksiyonu
7.2. Normal Dağılımın Özellikleri
7.3. Normal Rassal Değişkenlerin Aralık Olasılıkları
7.4. Standart Normal Dağılım
8.
MERKEZİ LİMİT TEOREMİ
5. NORMAL DAĞILIM
Günlük hayatta karşılaşılan birçok olayın olasılık yoğunluk fonksiyonu aritmetik
ortalama etrafında yüksek ve uçlara doğru ise azalan bir seyir göstermektedir. Bu tür
dağılımlara “Normal Dağılım” denir ve istatistik analizlerinde en çok kullanılandır.
Temel İstatiksel Kavramlar
Normal olasılık yoğunluk fonksiyonu aşağıdaki şekilde görüldüğü üzere aritmetik
ortalama etrafında simetrik bir dağılıma sahiptir. Normal olasılık yoğunluk fonksiyonu
çana benzediğinden “Çan Eğrisi” olarak ta adlandırılır.
Eğrinin kuyrukları x eksenini sonsuzda keser ve eğrinin altında kalan alan 1’e eşittir.
Süreklilik gösteren olayların dağılımına uygundur ve tek maksimuma sahip olduğu için
çarpıklık ve basıklık katsayıları kolaylıkla hesaplanabilir ki buda çalışmalarda büyük
kolaylıklar sağlar.
5.1. Normal Dağılım Olasılık Yoğunluk Fonksiyonu
X rassal değişkeninin Normal dağılımın olasılık yoğunluk fonksiyonu aşağıda
verilmiştir.
29
30
Sakarya Üniversitesi
𝑓 (𝑥 ) =
1
𝜎 √2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
,
- ∞ < x < ∞ için
Normal dağılımın olasılık yoğunluk fonksiyonunda yer alan sembollerin açıklanmaya
ihtiyacı vardır.
x = olasılığı hesaplanacak tesadüfi değişken
µ = X rassal değişkenin aritmetik ortalaması
σ2 = X rassal değişkeninin varyansı
e = 2.718 (tabii logaritmanın tabanı)
π = 3.141 (pi sayısı)
µ ve σ2, eksi sonsuz ile artı sonsuz arasında bir değer alabilir. Bundan dolayı tek bir
normal dağılım yoktur µ ve σ2 alacağı değerlere göre farklı olabilirler.
X rassal değişkeninin ortalaması µ ve varyansı σ2 olan normal dağılıma sahip ise bu
aşağıdaki şekilde gösterilir.
X N (μ ,σ2 )
X rassal değişkeninin istenilen bir aralıkta olma olasılığı aşağıdaki şekilde
hesaplanabilir.
𝑏
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝑎
1
𝜎√2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
𝑑𝑥
Temel İstatiksel Kavramlar
X rassal değişkenin normal dağılıma sahip olduğundan olasılıklar Z (Normal dağılım
tablosu) tablosu yardımıyla daha kolay hesaplanabilir. Z =
𝑥− µ
𝜎
olarak ifade edilebilir.
X rassal değişkeninin istenilen bir aralıkta olma olasılığı aşağıdaki şekilde de ifade
edilebilir.
𝑏
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝑎
1
𝜎√2𝜋
𝑒
−
𝑍2
2
𝑑𝑥
5.2. Normal Dağılımın Özellikleri
X rassal değişkeninin ortalaması µ ve varyansı σ2 olan normal dağılıma uyduğu
düşünülürse aşağıdaki özelliklere sahip olacaktır.
5. X rassal değişkeninin ortalaması E (X) = µ
6. X rassal değişkeninin varyansı Var (X) = E [ ( X- µ )2 ] = σ2
7. Skewness = 0 (Basıklık katsayısı)
8. Kurtosis = 3 (Çarpıklık Katsayısı)
X rassal değişkeninin dağılımın ortalaması ve varyansı bu değişkenin olasılık
fonksiyonunun şeklini belirler. Dağılımın iki parametresi olan ortalama ve varyansı
değiştikçe normal dağılım grafiğinin şeklide aşağıdaki örneklerde görüldüğü üzere
değişecektir.
31
32
Sakarya Üniversitesi
Şekil A’da normal dağılıma sahip ortalamaları aynı varyansları farklı iki tane olasılık
yoğunluk fonksiyonu verilmektedir. Şekilden de görüldüğü üzere varyans azaldıkça
olasılık yoğunluk fonksiyonu sivrileşmektedir (Basıklığı azalmaktadır).
Şekil B’de normal dağılıma sahip varyansları aynı ortalamaları farklı iki tane olasılık
yoğunluk fonksiyonu verilmektedir. Şekilden de görüldüğü üzere ortalama artıkça
yoğunluk fonksiyonu yana kayarken biçiminde herhangi bir değişme söz konusu
değildir.
Temel İstatiksel Kavramlar
Yukarıdaki şekilde X rassal değişkeninin olasılık yoğunluk fonksiyonu normal dağılıma
sahiptir ve dört farklı şekilde verilmiştir. Ortalama ve standart sapmadaki değişmelere
göre olasılık yoğunluk fonksiyonu eğrisinin değişimleri net olarak görülmektedir.
5.3.Normal Rassal Değişkenlerin Kümülatif (Birikimli) Olasılık
Fonksiyonu
Ortalaması
µ
ve varyansı σ2 olan normal dağılıma sahip bir X rassal değişkeninin
Kümülatif olasılık fonksiyonu F (x) = P ( X ≤ x0 ) olarak gösterilir.
X rassal değişkeninin belli bir x0 değerinde küçük olma olasılığını gösterir.
33
34
Sakarya Üniversitesi
Yukarıdaki şekilde gri taralı alan,
normal dağılıma sahip X rassal değişkeninin
herhangi bir x0 değerinden küçük olma olasılığını vermektedir. Bu alan aşağıdaki genel
formül yardımıyla bulunabilir.
𝑥0
𝐹 (𝑥 ) = 𝑃 (𝑋 ≤
𝑥0 )
= ∫
−∞
1
𝜎√2𝜋
(𝑥− µ)2
−
𝑒 2𝜎2
𝑑𝑥
5.4.Normal Rassal Değişkenlerin Aralıklı Olasılık Fonksiyonu
Ortalaması µ ve varyansı σ2 olan normal dağılıma sahip bir X rassal değişkeninin
aralıklı olasılık fonksiyonu F (a) – F (b) = P ( a < X < b ) olarak gösterilir.
X rassal değişkeninin a ve b gibi iki değer arasında olma olasılığını gösterir (a < b
koşuluyla).
Temel İstatiksel Kavramlar
Yukarıdaki şekilde gri taralı alan, normal dağılıma sahip X rassal değişkeninin a ve b
gibi iki değer arasında olma olasılığını vermektedir. Bu alan aşağıdaki genel formül
yardımıyla bulunabilir.
𝑏
𝑓(𝑥 ) = 𝑃 (𝑎 < 𝑋 < 𝑏) = ∫
𝑎
1
𝜎√2𝜋
𝑒
−
(𝑥− µ)2
2𝜎2
𝑑𝑥
35
36
Sakarya Üniversitesi
Dağılım normal bir dağılımsa o zaman aşağıdaki normal dağılım tablosu kullanılır.
Temel İstatiksel Kavramlar
5.5.Standart Normal Dağılım
Normal olasılık fonksiyonlarını hesaplamak bazı güçlükler içerdiğinden her seferinde
bilgisayar yardımıyla sayısal yöntemler kullanılarak hesaplamamız gerekir. Bu işlemi
yapmak yerine standart normal dağılım (Z) tablosu kullanılabilir. Bu tablolarda her bir
37
38
Sakarya Üniversitesi
normal olasılık dağılımının olasılıkları çizelgeleştirilmiş ve tek bir normal dağılım
olasılıklarıyla ifade edilmiştir.
X ortalaması 0 ve varyansı 1 olan normal rassal değişken ise Standart normal dağılıma
(Z) sahip demektir ve aşağıdaki şekilde gösterilir.
Z N (μ=0 ,σ2 =1)
X rassal değişkeninin Normal dağılımın olasılık yoğunluk fonksiyonu aşağıda
verilmiştir.
𝑓 (𝑧) =
1
√2𝜋
𝑒
−
𝑍2
2
,
- ∞ < x < ∞ için
Standart normal dağılımın olasılık yoğunluk fonksiyonunda yer alan sembollerin
açıklanmaya ihtiyacı vardır.
Z=
𝑋− µ
𝜎
E (Z) = µ = 0
Var (Z) = σ = 1
Z değeri belirli bir değerin aritmetik ortalamadan kaç standart sapma aşağıda ya da
yukarıda olduğunu belirlemek için kullanılır.
Temel İstatiksel Kavramlar
Yukarıdaki iki şekilde standart normal dağılıma sahiptir. Standart normal dağılım
Özellikleri:
1. Dağılım ortalamaya göre simetriktir. %50'si sağda, %50'si soldadır.
2.Normal dağılım eğrisinin altında kalan alan 1’e eşittir.
3. Aritmetik ortalama, ortanca, tepe değer (mod) birbirine eşittir ve maksimum
yüksekliğin bulunduğu yerdedir.
4. Normal dağılımı gösteren değişkenlerin aldıkları değerlerin;
Gözlemlerin %68 ‘ i ortalama ile 1 standart sapma aralığına,
Gözlemlerin %95‘ i ortalama ile 2 standart sapma aralığına, ve
Gözlemlerin %99 ‘ i ortalama ile 3 standart sapma aralığına düşer.
Normal Dağılımın Standart Normal Dağılıma Çevrilmesi
Normal dağılımları standart normal dağılımlara kolaylıkla çevirebiliriz. Bu çevirme
işleminden sonrada olasılıkları standart normal dağılım (Z) tablosu yardımıyla
bulabiliriz.
ÖRNEK 1:
39
40
Sakarya Üniversitesi
Sakarya Üniversitesi öğrencilerinin gelirleri normal dağılıma sahiptir. Ortalamasının (μ)
400 ve standart sapmanın (σ) 50 olduğu bilindiğine göre tesadüfü seçilen bir öğrencinin
geliri 500 (X) olsun. Bu normal dağılımı standart normal dağılıma çeviriniz.
Z=
𝑋− µ
𝜎
=
500−400
50
=2
Bu durumda seçilen öğrencinin geliri, ortalamadan 2 standart sapma daha yüksektir.
ÖRNEK 2:
Sakarya Üniversitesi öğrencilerinin gelirleri normal dağılıma sahiptir. Ortalamasının (μ)
400 ve standart sapmanın (σ) 50 olduğu bilindiğine göre tesadüfü seçilen bir öğrencinin
geliri 350 (X) olsun. Bu normal dağılımı standart normal dağılıma çeviriniz.
Z=
𝑋− µ
𝜎
=
350−400
50
= −1
Bu durumda seçilen öğrencinin geliri, ortalamadan 1 standart sapma düşüktür.
Temel İstatiksel Kavramlar
Standart normal dağılım tablosu aşağıda verilmiştir. Bu tabloyu okumayı bilmemiz
gerekir.
Z tablosu
•Artı eksi 3.49 arasında değişiyor.
•Bu, teorik evrenin %99.98’ine karşılık geliyor.
•Z tablosu 1/10’luk aralarla standart sapmayı gösteriyor
•Araştırmacılar z tablosundaki birkaç değerle ilgilenir. Çünkü çoğu hipotez testlerinde
%95 ve %99’luk alanlarla ilgileniyor.
Tablo 1. Standart normal dağılım tablosu
z
.0
.01
.02
.03
.04
.05
.06
.07
.08
.09
.0
.5000
.5040
.5080
.5120
.5160
.5199
.5239
.5279
.5319
.5359
.1
.5398
.5438
.5578
.5517
.5557
.5596
.5636
.5675
.5714
.5753
41
42
Sakarya Üniversitesi
.2
.5793
.5832
.5871
.5910
.5948
.5987
.6026
.6064
.6103
.6141
.3
.6179
.6217
.6255
.6293
.6331
.6368
.6406
.6443
.6480
.6517
.4
.6554
.6591
.6628
.6664
.6700
.6736
.6772
.6808
.6844
.6879
.5
.6915
.6950
.6985
.7019
.7054
.7088
.7123
.7157
.7190
.7224
.6
.7257
.7291
.7324
.7357
.7389
.7422
.7454
.7486
.7517
.7549
.7
.7580
.7611
.7642
.7673
.7704
.7734
.7764
.7794
.7823
.7852
.8
.7881
.7910
.7939
.7967
.7995
.8023
.8051
.8078
.8106
.8133
.9
.8159
.8186
.8212
.8238
.8264
.8289
.8315
.8340
.8365
.8389
1.0
.8413
.8438
.8461
.8485
.8508
.8531
.8554
.8577
.8599
.8621
1.1
.8643
.8665
.8686
.8708
.8729
.8749
.8770
.8790
.8810
.8830
1.2
.8849
.8869
.8888
.8907
.8925
.8944
.8962
.8980
.8997
.9015
1.3
.9032
.9049
.9066
.9082
.9099
.9115
.9131
.9147
.9162
.9177
1.4
.9192
.9207
.9222
.9236
.9251
.9265
.9279
.9292
.9306
.9319
1.5
.9332
.9345
.9357
.9370
.9382
.9394
.9406
.9418
.9429
.9441
1.6
.9452
.9463
.9474
.9484
.9495
.9505
.9515
.9525
.9535
.9545
Temel İstatiksel Kavramlar
1.7
.9554
.9564
.9573
.9582
.9591
.9599
.9608
.9616
.9625
.9633
1.8
.9641
.9649
.9656
.9664
.9671
.9678
.9686
.9693
.9699
.9706
1.9
.9713
.9719
.9726
.9732
.9738
.9744
.9750
.9756
.9761
.9767
2.0
.9772
.9778
.9783
.9788
.9793
.9798
.9803
.9808
.9812
.9817
2.1
.9821
.9826
.9830
.9834
.9838
.9842
.9846
.9850
.9854
.9857
2.2
.9861
.9864
.9868
.9871
.9875
.9878
.9881
.9884
.9887
.9890
2.3
.9893
.9896
.9898
.9901
.9904
.9906
.9909
.9911
.9913
.9916
2.4
.9918
.9920
.9922
.9925
.9927
.9929
.9931
.9932
.9934
.9936
2.5
.9938
.9940
.9941
.9943
.9945
.9946
.9948
.9949
.9951
.9952
2.6
.9953
.9955
.9956
.9957
.9959
.9960
.9961
.9962
.9963
.9964
2.7
.9965
.9966
.9967
.9968
.9969
.9970
.9971
.9972
.9973
.9974
2.8
.9974
.9975
.9976
.9977
.9977
.9978
.9979
.9979
.9980
.9981
2.9
.9981
.9982
.9982
.9983
.9984
.9984
.9985
.9985
.9986
.9986
3.0
.9987
.9987
.9987
.9988
.9988
.9989
.9989
.9989
.9990
.9990
3.1
.9990
.9991
.9991
.9991
.9992
.9992
.9992
.9992
.9993
.9993
43
44
Sakarya Üniversitesi
3.2
.9993
.9993
.9994
.9994
.9994
.9994
.9994
.9995
.9995
.9995
3.3
.9995
.9995
.9995
.9996
.9996
.9996
.9996
.9996
.9996
.9997
3.4
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9998
Yukarıdaki tabloda çeşitli Z değerleri için normal eğrilerin alanlarını hesaplanmıştır. Bu
tablolar yardımıyla doğrudan olasılıkları hesaplayabiliriz bunun için Z tablosunu
okumasını bilmemiz gerekir. Z tablosunun nasıl okunacağını aşağıdaki örnekler
yardımıyla daha iyi anlayabiliriz.
0.5 sayısı. 5 şeklinde yazılabilir. Aynı şekilde 0.59 sayısı. 59 şeklinde yazılabilir.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z<0.68) olduğunu
varsayalım. Bunun için ilk önce mavi dikey ve mavi yatay sütunlara bakmalıyız.
0.68 bu sütunlarda .6 ve .08 noktalarının (.6 + .08 = .68) kesiştiği yerde aranır.
Böylece P(Z<0.68) = .7517 deriz.
Temel İstatiksel Kavramlar
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z<1.36) olduğunu
varsayalım. Bunun için ilk önce mavi dikey ve mavi yatay sütunlara bakmalıyız.
1.36 bu sütunlarda 1.3 ve .06 noktalarının (1.3 + .06 = 1.24) kesiştiği yerde
aranır. Böylece P(Z<1.36) = .9131 deriz.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z>2.18) olduğunu
varsayalım. Bu olasılığı tabloda arayabilmenin tek koşulu P(Z<Z0) şeklinde
yazılabilmesidir. P(Z>2.18) = 1 - P(Z<2.18) = 1- 0.9854 = 0.0146 şeklinde
bulunur.
45
46
Sakarya Üniversitesi
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z< -1.36)
olduğunu varsayalım. Bu olasılığı tabloda arayabilmenin tek koşulu aranan
değerin pozitif olmasıdır. P(Z<-1.36) = 1 - P(Z<1.36) = 1- 0.9131 = 0.0869
şeklinde bulunur.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(Z>-2.96)
olduğunu varsayalım. Normal dağılımın simetri özelliğinden bu dağılım
P(Z<2.96) şeklinde yazılabilir.
Standart normal dağılıma dönüştürülen bir normal dağılımın P(1.36<Z<1.96)
olduğunu varsayalım. Bu aralıklardaki olasılık P(Z<1.96) - P(Z<1.36) = 0.97500.9131 =0.0619 şeklinde bulunur.
Temel İstatiksel Kavramlar
Standart normal dağılıma dönüştürülen bir normal dağılımın P(-1.26<Z<1.26)
olduğunu varsayalım. Bu aralıklardaki olasılık P(Z<1.26) - [ 1 - P(Z<1.26) ] =
2P(Z<1.28) - 1 şeklinde bulunur.
6. MERKEZİ LİMİT TEOREMİ
Normal dağılıma sahip rassal değişkenlerde gözlem sayısı (n) artıkça rassal değişken
standart normal dağılıma yaklaşır.
47
48
Sakarya Üniversitesi
Değerlendirme Soruları
1 -Ortalaması 60 varyansı 49 olan bir not popülasyonunda notu 81 olan bir
öğrencinin standart z notu kaçtır?
Çözüm= z hesaplaması formülü için bize gerekli olanlar standart sapma, popülasyon ve
ortalama. İşlemde elimizde ortalama var 60, popülasyon var 81 ve burada standart
sapma yerine varyans verilmiş 49; standart sapma varyansın karekökü olduğu için
varyansın karekökünü aldığımızda standart sapmayı da bulmuş olacağız 49’un
karekökü=7.
Şimdi formülümüz z=ortalama-popülasyon/standart sapma yani: z=x-μ/σ , elimizde olan
rakamları formüldeki yerlerine oturtup işleme başlarsak z=81-60/7=21/7=3
2- Ortalaması 75 varyansı 25 olan bir not popülasyonunda 85 alan bir Öğrencinin
standart Z notu nedir?
A) 1
B) 0
C) 10
D) 2
E) 5
Açıklama: varyansı 25 ise standart sapması 5 olur.
3- Ağırlık, boy, kolesterol değeri, hız gibi değişkenlerin teorik popülasyon
dağılımının genel adı nedir?
A) Binom dağılımı B) Kalitatif dağılım C) Poisson dağılımı
D) Kesikli dağılım E) Sürekli Normal dağılım
4- Standart Normal dağılış ile ilgili aşağıdakilerden hangisi doğrudur?
a) Basıklık 3’tür
b) Simetriktir
c) Normal dağılıştan standart normal dağılış türetilmiştir
d) Standart normal dağılışın ortalaması 0 ve varyansı 1’dir
e) Hepsi
5- Standart normal dağılışın ortalaması nedir?
a) Her zaman 0 dır
b) Her zaman 1 dir
c) Özelliğe göre değişir
d) Ölçümlere bağlıdır e) Bilinmez
6- Standart Z dağılışı için aşağıdaki ifadelerden hangisi doğrudur?
a) Sağa çarpıktır
b) Açık U şeklindedir
c) Simetriktir
d) Sola çarpıktır
e) Belirli bir şekli yoktur
Temel İstatiksel Kavramlar
7- Standart normal Z dağılışının varyansı nedir?
A) Özelliğe göre değişir. B) Her zaman 1 dir
C) Her zaman 0 dır.
D) Ölçümlere bağlıdır
E) Bilinmez
8- Bir deneyde standart sapma 5, ortalama 50 bulunmuştur buna göre x=42 hangi
standart değere dönüşür?
A)0,2
B)0,3
C)0,4
D)0,5
E)-1,6
9- Ortalaması 25 varyansı 4 olan bir dağılımda x=30 değeri hangi standart değere
dönüşür?
A)-2,5
B)5
C)2,5
D)1
E)2
Kaynakça
1. Yılmaz Özkan, Uygulamalı İstatistik 1, Sakarya Kitapevi, 2008.
2. Özer Serper, Uygulamalı İstatistik 1, Filiz Kitapevi, 1996.
3. Meriç Öztürkcan, İstatistik Ders notları, YTÜ.
4. Andım Oben Balce ve Serdar Demir, İstatistik Ders Notları, Pamukkale
Üniversitesi, 2007.
5. Ayşe Canan Yazıcı, Biyoistatistik Ders Notları, Başkent Üniversitesi.
6. Zehra Muluk ve Yavuz Eren Ataman, Biyoistatistik ve Araştırma Teknikleri
Ders Notları, Başkent Üniversitesi.
49
50
Sakarya Üniversitesi