PowerPoint Sunusu - Başkent Üniversitesi
advertisement

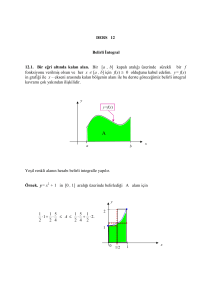
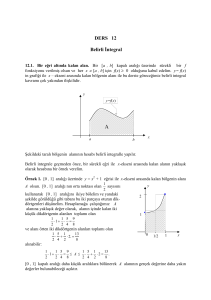
TBF 121 - Genel Matematik I DERS – 12: Belirli İntegral Prof. Dr. Halil İbrahim Karakaş Başkent Üniversitesi Bir eğri altında kalan alan. Bir [a , b] kapalı aralığı üzerinde sürekli bir f fonksiyonu verilmiş olsun ve her x [a , b] için f(x) 0 olduğunu kabul edelim. y = f(x) in grafiği ile x – ekseni arasında kalan bölgenin alanı ile bu derste göreceğimiz belirli integral kavramı çok yakından ilişkilidir. y y y=f(x) 2 1 A a b x 0 1/2 1 Yeşil renkli alanın hesabı belirli integralle yapılır. Örnek. y = x2 + 1 in [0 , 1] aralığı üzerinde belirlediği A alanı için 1 1 5 1 5 1 1 A 2 9 A 13 2 2 4 2 4 2 8 8 x Belirli İntegral, Riemann Toplamları. Bir [a , b] kapalı aralığı üzerinde sürekli bir f fonksiyonu verilmiş olsun. y (c1 , f(c1)) a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b ck (xk-1 , xk) , 1 k n xk = xk – xk-1 , 1 k n c2 c1 x0 = a x1 cn-2 c3 x2 x3 xn-3 cn-1 xn-2 cn xn-1 b =xn x y = f(x) Tn = f(c1) x1 + f(c2) x2 + . . . + f(cn) xn = denir. n f (c )x k 1 k k toplamına bir Riemann Toplamı y (c1 , f(c1)) a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b ck (xk-1 , xk) , 1 k n xk = xk – xk-1 , 1 k n c2 c1 x0 = a x1 cn-2 c3 x2 x3 xn-3 cn-1 xn-2 cn xn-1 b =xn x y = f(x) Riemann Toplamı: Tn = f(c1) x1 + f(c2) x2 + . . . + f(cn) xn = xk n f (c )x k 1 k k lardan her biri sıfıra yaklaşırken (ki bu durumda n sayısı da sonsuza ıraksar) Tn Riemann Toplamı’nın limit değerine f fonksiyonunun [a , b] kapalı aralığı üzerinde belirli integrali (definite integral) denir ve bu integral sembolü ile gösterilir. b a f (x) dx integralin üst sınırı integralin alt sınırı y (c1 , f(c1)) a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b ck (xk-1 , xk) , 1 k n xk = xk – xk-1 , 1 k n c2 c1 x0 = a x1 cn-2 c3 x2 x3 xn-3 cn-1 xn-2 cn xn-1 b =xn y = f(x) Riemann Toplamı: n Tn = f(c1) x1 + f(c2) x2 + . . . + f(cn) xn = f (c k 1 k )x k Belirli İntegral: b a f (x) dx lim Tn x k 0 lim x k 0 f (c1 )x1 f (c2 )x2 f (cn )xn x Eğer her x [a , b] için f(x) 0 ise, b f (x)dx belirli integrali [a , b] aralığı üzerinde y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir. a y y = f(x) b A f (x) dx A a f(x) 0 a b , x [a , b] x b b Eğer her x [a , b] için f(x) ≤ 0 ise, ( f (x))dx f (x) dx belirli integrali [a , b] aralığının a a altında y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir. y a b x A y = f(x) f(x) 0 , x [a , b] b A f (x) dx a Genel Durum: y A a C c d b x B y = f(x) b c d b a c d a f (x)dx A B C f (x)dx f (x)dx f (x)dx y (c1 , f(c1)) a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b ck (xk-1 , xk) , 1 k n xk = xk – xk-1 , 1 k n c2 c1 x0 = a x1 cn-2 c3 x3 x2 xn-3 cn-1 xn-2 cn xn-1 b =xn x n Tn f (ck )x k y = f(x) k 1 Özellikler: • 1. Eğer her x [a , b] için f(x) 0 ise, b f (x)dx a belirli integrali [a , b] aralığı üzerinde y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir. • 2. k f (x)dx k f (x)dx • 3. f (x) g(x)dx f (x)dx g(x)dx b b a a b b b a a a • 4. a < c < b için b c b a a c f (x)dx f (x)dx f (x)dx Kalkülüs’ün Temel Teoremi(Fundamental Theorem of Calculus). Bu teorem belirli integral ile belirsiz integral arasındaki ilişkiyi verir: Kalkülüs’ün Temel Teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ve f nin bir ters türevi F ise, b f (x)dx F (b) F (a) a dir. Kalkülüs’ün Temel Teoreminden belirli integral için bir özellik daha yazabiliriz: b F (x) a F (b) F (a) Gösterim. F ' (x) f (x) Örnek. 0 2x 1dx 1 • 5. b a a b f (x)dx f (x)dx b b f ( x ) dx F (x) a F (b) F (a) a x x 1 1 0 0 2. 2 1 0 Kalkülüs’ün Temel Teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ve f nin bir ters türevi F ise, b b a a f (x)dx F (x) F (b) F (a) dir. Örnek. 1 x3 4 1 2 x 1 dx x 1 0 0 . 0 3 3 3 0 1 y 2 y = x2+1 4 A x 2 1dx . 0 3 1 1 A 0 1 x 4 2 x x 2 2 x 3 e dx x 3e 4 ln x 1 1 x 4 3e 2 4 ln 2 1 3e 0 2 3(1 e 2 e) 4 ln 2. 6 0 2x dx ? x2 4 u = x2 + 4 6 0 , du = 2x dx . 2x 1 dx du ln u ln x 2 4 C 2 x 4 u 6 2x 2 dx ln x 4 ln 40 ln 4 ln 10. 2 0 x 4 Belirli integralde değişken değiştirme. Son örneğimizde belirli integrali hesaplarken, ters türevin, yani belirsiz integralin belirlenmesinde değişken değiştirme yöntemini kullandık. Bu yöntemi doğrudan doğruya belirli integral üzerinde de uygulayabiliriz. Hatta bu durumda zaman kazanılacağı da söylenebilir. b F '(g(x))g'(x)dx a g (b) g (a ) F '(u) du F (u) g(a) F (g(b)) F (g(a)) g (b) u = g(x) , du = g´(x) dx x = a u = g(a) ; x = b u = g(b) Son örneğimizi bu yolla yapalım: 2x 0 x 2 4 dx 6 40 4 1 40 du ln u 4 ln 40 ln 4 ln 10. u u = x2 + 4 , du = 2x dx x = 0 u = 4 ; x = 6 u = 40 Başka bir örnek: 4 1 3 2 1 x 3x 1 dx 1 u du 1 u3 0 6 6 2 4 2 1 u 9 3 4 2 1 7 8 1 . 9 9 1 1 u = 3x2 + 1 , du = 6x dx , x dx = (1/6) du x=0 u=1 ; x=1 u=4 Başka bir örnek: e 1 0 3x 3x e 3 x 1dx e 3 1 3 3 2 e 3 1 1 u u du 3 2 3 1 e 3 3 1 2 1 1 u2 e 3 3 . 6 6 6 1 u = e3x – 3x , du = (3e3x – 3) dx , (e3x – 1) dx = (1/3) du x=0 u=1 ; x = 1 u = e3 - 3 Uygulama. Haftada x televizyon ünitesi üreten bir işletmenin haftalık marjinal kârı K´(x) = 165 - (0.1)x , 0 x 4000 olarak veriliyor. Şu anda haftada 1500 ünite üreten firma, haftalık üretimini artırmak istiyor. Haftalık üretimini 1600 e çıkarırsa, haftalık kârındaki değişim ne olacaktır? Para birimi TL olsun. Çözüm. Kârdaki artış 1600 K (1600) K (1500) K (x) 1500 1500 K '(x) dx 1600 165 0.1x dx 165x 0.05x 2 1500 1500 1600 1600 165 1 600 0.05 2 560 000 165 1 500 0.05 2 250 000 16500 0.05 31 000 16500 15 500 1000 TL olur. Daha önce belirsiz integral hesabında kullandığımız kısmî integrasyon yöntemini belirli integral hesaplarken de kullanabiliriz. Örnek. 1 0 u=x , du = dx x e x dx u dv uv vdu xe x e x dx dv = ex xe e x dx x 1 0 0 1 1. , v = ex Bazı integrallerin hesabında değişken değiştirme ve kısmî integrasyon yöntemleri birlik-te kullanılabilir. Örnek. 2 1 1 1 2 2 1 x ln x 1 dx ln t dt ln t dt t ln t t dt 0 1 2 2 1 2 t 1 2 t = x2 + 1 , dt = 2x dx , x dx = (1/2) dt x=0 t=1 , x=1t=2 u = ln t , dv = dt du = (1/t) dt , v = t 1 1 t ln t t 2ln 2 2 0 1 2 2 1 1 1 2ln 2 1 ln2 . 2 2 Örnek. 1 e 0 t x , dt x dx 1 t x x 1 2 te dt 2 te dt xe e 0 0 1 1. 0 t 1 0 1 dx , dx 2 x dt 2tdt 2 x x 0t 0 , x 1t 1 İntegral için ortalama değer teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ise, öyle bir c (a , b) vardır ki y b f (x)dx (b a) f (c) a dir. (c , f(c)) b 1 f (c) f (x) dx a (b a) a c f fonksiyonunun [a , b] aralığı üzerinde ortalama değeri (Average value of f on the interval [a , b] ) Örnek. f(x) = x2 - 3x + 4 ün [-1 , 1] aralığı üzerinde ortalama değeri 1 2 1 1 x3 3 2 2 f (c) (x 3x 4) dx ( x 4 x) 1 (1 (1)) 2 3 2 1 11 3 1 3 11 4 ( 4) . 23 2 3 2 3 b x Örnek. Fiyat–talep fonksiyonu p 500e ( 0.01) x olarak verilmişse, [200,300] talep aralığı üzerinde ortalama fiyatın ne olduğunu belirleyelim. Para birimi TL olsun. Verilen aralıktaki ortalama fiyat p ile gösterilirse, 300 300 1 500 300 (0.01) x ( 0.01) x ( 0.01) x p 500 e dx e dx 5 e dx 200 200 200 (300 200) 100 ( 0.01) x 300 e 5 0.01 500e ( 0.01) x 300 200 500(e 3 e 2 ) 42.77 TL. 200 Alan Hesabı. Bir eğri ile x - ekseni arasında kalan alan. y y = f(x) b A f (x) dx a A a b f(x) 0 x , x [a , b] y a b x A y = f(x) f(x) 0 , x [a , b] b A f (x) dx a Alan Hesabı. Bir eğri ile x-ekseni arasında kalan alan. y y = f(x) a b c x d Boyalı Alan : A b c d a b c A f (x) dx f (x) dx f (x) dx Örnek. f(x) = 3 + 2x – x2 , 0 x2 ile verilen bölgenin alanı. y y = 3+2x – x2 A 3 2 x x 2 dx 3x x 2 2 0 x 3 A 23 13 2 3 2 2 3 1 1 3 3 2 0 2 x 7 11 6 . 3 3 3 2 0 Örnek. f(x) = x2 - 2x - 5 , 0 x 3 ile verilen bölgenin alanı. y A x 2 2 x 5 dx 3 0 1 3 0 x 3 x 2 x 5x 3 0 3 A y = x2 – 2x - 5 27 9 15 0 15. 3 Örnek. f(x) = x2 - 2x , -1 x 1 y ile verilen bölgenin alanı. A x 2 x dx x 2 2 x dx 0 1 2 1 0 y = x2 – 2x 3 1 1 1 0 1 1 0 3 3 1 -1 0 x x 2 2 x x 3 1 3 0 3 x 1 1 1 1 2. 3 3 Örnek. f(x) = xex , -1 x 1 ile verilen bölgenin alanı. y 0 1 A xe dx xe x dx x 1 0 y = xex (x 1)e x 0 1 (x 1)e x 1 0 1 2e 1 0 (1) 1 -1 x 2 2 . e Örnek. f (x) 2x , 2 x 4 -2 x 2 ile verilen bölgenin alanı. f (x) y 2x x2 4 –2 x 2 2 2x 2x A 2 dx 2 dx 2 x 4 0 x 4 0 ln( x 4) 2 0 2 ln( x 4) 2 2 0 (ln 4 ln 8) (ln 8 ln 4) 2ln2 ln 4. İki Eğri Arasında Kalan Alan. f ve g , [a , b ] aralığında sürekli fonksiyonlar, her x [a , b ] için g(x) f(x) olsun . Bu durumda y = f(x) in grafiği y = g(x) in grafiğinin yukarısındadır ve [a , b ] aralığı üzerinde bu iki eğri arasında kalan alan integral olarak şöyle ifade edilir: y = f(x) y A A f (x) g(x) dx b a y = g(x) a b x Örnek. f(x) = x + 2 , g(x) = -x2 + 1 , 0 x 2 y y=x+2 ile verilen bölgenin alanı. A x 2 x 2 0 2 1 dx x 2 x 1 dx A 2 0 1 2 y = -x2 + 1 x 2 x x x 3 2 0 3 2 8 20 22 . 3 3 İki eğri arasında kalan alan hesaplanırken, y = f(x) in grafiğinin bir kısmı y = g(x) in grafiğinin yukarısında, bir kısmı da aşağısında olabilir. Bu durumda söz konusu aralık alt aralıklara bölünerek alan hesaplanır. Örnek olarak aşağıdaki şekilde gösterilen bölgenin alanına bakalım. y = f(x) y a c b x A : Boyalı alan y = g(x) A f (x) g(x) dx g(x) f (x) dx c b a c Örnek. f(x) = -x + 1 , g(x) = x2 - 1 , 0 x 2 A y 1 0 ile verilen bölgenin alanı. x 1 x 2 1 dx x x 2 dx 1 y = x2 - 1 2 0 1 2 1 2 1 x 2 x 2 1 x 1 dx x 2 dx 2 x x x x 2 x 2 x 3 2 0 3 2 1 3 2 3 2 1 1 8 1 1 2 0 2 4 2 3 2 3 3 2 3. 1 y = -x + 1 2 x Hacim Hesabı , Dönel Cisimlerin Hacmi. Düzlemde bir bölgenin x-ekseni etrafında döndürülmesiyle meydana gelen cismin hacmi integral yardımıyla hesaplanabilir. y = f(x) y Cismin Hacmi : V f(x) a dx V f (x)2 dx b b Silindirin Hacmi : dV dV f (x)2 dx x a Örnek. f(x) = x2 , 0 x 1 ile verilen bölgeyi x - ekseni etrafında döndürünce meydana gelen cismin hacmini hesaplayalım. y y= V x 1 x2 2 2 0 dx 1 x 4 dx 0 5 1 1 x x 5 0 . 5 Örnek(Kürenin hacmi). Yarıçapı r birim olan küre, yarıçapı r birim olan bir yarım çemberin çapı etrafında döndürülmesiyle elde edilir. Dolayısıyla, sözü edilen hacim f(x) = (r2 - x2 )1/2 , -r x r eğrisinin x - ekseni etrafında döndürülmesiyle elde edilir. y y r 2 x2 V r r r r r r 2 2 x dx 2 2 x 2 dx r x -r r 2 x3 r x 3 r 3 r3 3 r3 r r 3 3 4 r 3 . 3 Örnek(Koninin hacmi). Taban yarıçapı r birim ve yüksekliği h birim olan koni, f(x) = (r/h)x , 0 x h eğrisinin x - ekseni etrafında döndürülmesiyle elde edilir. V (r / h)x 2 dx h y 0 y (r / h)x h 0 r2 2 2 x dx h h x h r x 2 h 3 0 r 2 h3 2 h 3 2 r h. 3 2 3 Rant. Pazarda, bir üründen yüksek fiyatla daha az müşteriye satılarak veya düşük fiyatla daha çok satın alınarak sağlanan faydaya toplam rant denir. Kimi üretici ürününü pazar denge fiyatının altında bir fiyata satmaya razı iken pazarda oluşan daha yüksek fiyattan satabilerek daha çok kazanç sağlamış olur. Üretici lehine oluşan bu kazanç, üretici rantı olarak bilinir. Kimi tüketici de pazardaki bir ürünü pazar denge fiyatından daha yüksek fiyata satın almaya razı iken pazarda oluşan daha düşük fiyattan satın alabilerek bir tür kazanç sağlamış olur. Tüketici lehine oluşan bu kazanç da tüketici rantı olarak bilinir. Belli bir piyasada fiyat–arz fonksiyonu p = A(x), fiyat–talep fonksiyonu p = T(x), pazar denge fiyatı p0 TL ve bu denge fiyatına karşılık gelen ürün miktarı x0 birim ise, bu piyasadaki üretici ve tüketicilerin sağlayabilecekleri toplam rant aşağıdaki şekil yardımıyla açıklanacaktır. p T(0) (x,T(x)) x0 Rt (T (x) p0 )dx (x,p0) TÜKETİCİ RANTI 0 p=A(x)) p0 ÜRETİCİ RANTI p=T(x)) (x,A(x)) A(0) x x0 x0 x Rü (p0 A(x))dx 0 Örnek. Bir piyasanın fiyat–arz fonksiyonu p(x) = 4x + x2 ve fiyat–talep fonksiyonu p(x) = 1200 - 72x - x2; para birimi TL dir. Bu piyasanın a) pazar denge fiyatını b) toplam üretici rantını c) toplam tüketici rantını bulalım. a) Arz ve talebin çakıştığı ürün miktarı 1200 72 x x 2 4 x x 2 2 x 2 76 x 1200 0 2(x 2 38 x 600) 0 2(x 50)(x 12) 0 x 12 O halde, pazar denge fiyatı p0 122 4 12 192 TL. b) toplam üretici rantı 12 12 0 0 Rü (192 (x 2 4 x))dx (192 4 x x 2 )dx x3 2 192x 2 x 3 12 2304 288 576 1440 TL. 0 c) toplam tüketici rantı 12 12 0 0 Rt (1200 72 x x 2 192)dx (1008 72 x x 2 )dx x3 2 1008 x 36 x 3 12 12096 5184 576 6336 0 TL. Gelir Dağılımı – Lorenz Eğrisi. Bir ülkede milli gelirin ülke bireylerince nasıl bölüşüldü-ğü, bölüşümün adil olup olmadığının belirlenmesi için uygulanan çeşitli yöntemler vardır. Bu yöntemlerden biri, nüfusun yüzde kaçının milli gelirin yüzde kaçını aldığının belirlenmesi ve grafikle gösterilmesidir. Bu şekilde elde edilen grafiğe, yöntemi ilk uygulayan ve geliştiren Amerikalı istatistikçi Max Otto Lorenz’e atfen Lorenz eğrisi adı verilmiştir. Lorenz eğrisi şöyle oluşturulur: Ülkedeki bireyler milli gelirden aldıkları pay miktarına göre (küçükten büyüğe) sıralanırlar. Ülke nüfusu N ise ve 0 ≤ x ≤ N olmak üzere x t N ise, bu sıralamaya göre ilk x birey nüfusun yüzde 100t lik dilimini oluşturur. Örneğin, ülke nüfusu 75 milyon ise, ilk 15 milyon kişi, nüfusun yüzde 100(15/75)=20 lik dilimini oluşturur. İlk x bireyin gelirleri toplamı g(x), milli gelirin tamamı g(N) = G ise, ilk x bireyin milli, gelirden aldıkları pay g(x) L G olmak üzere yüzde 100L olur. Örneğin, yukarıda sözü edilen ülkenin nüfusunun gelir dağılımına göre ilk yüzde yirmilik dilimini oluşturan 15 milyon kişinin toplam geliri 51 milyar dolar ve ülkenin milli geliri 850 milyar dolar ise, nüfusun yüzde yirmilik dilimi milli gelirin yüzde 100(51/850)=6 sını almaktadır. t x g( x ) , L , 0 t 1, 0 L 1. N G g(Nt ) Lorenz Fonksiyonu. G L(t ) Lorenz fonksiyonunun tanım kümesi [0,1] aralığı, görüntü kümesi de [0,1] aralığıdır. y A 1 y=t y = L(t) O 1 B Lorenz Eğrisi t Gelir dağılımının ne dereceye kadar adil olduğunu belirlemek için şu orana bakılır: 1 1 taranan alan 0 (t L(t ))dt 2 (t L(t ))dt. 0 OAB nin alani 1/2 0 1 olduğuna dikkat ediniz. Gini katsayısı Örnek. İki ülkede gelir dağılımına ilişkin yapılan çalışmada Lorenz fonksiyonları birinci ülke için L1 (t ) (0.93)t 2 (0.07)t ikinci ülke için L2 (t ) (0.99)t 2 (0.01)t olarak elde ediliyor. Hangi ülkede gelir dağılımı daha adildir? Birinci ve ikinci ülke için Gini katsayıları, sırasıyla 1 1 2 (t L1 (t )) dt 0 1 t3 t2 2 2 ((0.93)t (0.93)t ) dt 1.86( ) 1.86( 1 1 ) 1.86 0.31 0 3 2 0 3 2 6 1 1 3 2 t t 2 2 2 (t L2 (t )) dt 2 ((0.99)t (0.99)t ) dt 1.98( ) 1.98( 1 1 ) 1.98 0.33 0 0 3 2 0 3 2 6 1 1 2 1 Birinci ülkenin gelir dağılımı ikinci ülkenin gelir dağılımına göre daha adil.